Movimento circular uniforme (M.C.OU.) fórmulas, características

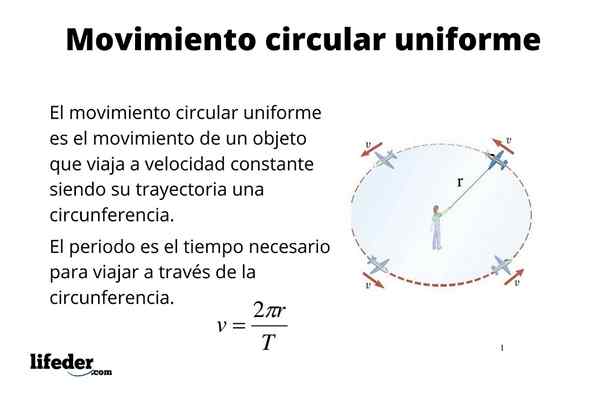
Uma partícula tem movimento circular uniforme (M.C.OU.) Quando sua trajetória é uma circunferência e também a viaja constantemente. Numerosos objetos como peças de máquinas e motores, por exemplo, têm esse tipo de movimento, entre os quais os discos duros dos computadores, os fenateros, eixos e muito mais coisas são mais.

O movimento circular uniforme também é uma boa abordagem para o movimento de alguns corpos celestes, como a terra. A órbita da Terra é realmente elíptica, como as leis de Kepler apontam. No entanto, a excentricidade da órbita é pequena e, como primeira abordagem, pode ser considerada circular, o que simplifica alguns cálculos, como encontrar a velocidade da terra quando se move ao redor do sol.

Na descrição do movimento circular uniforme, os mesmos parâmetros são usados ​​como no movimento retilíneo, a saber: posição, deslocamento, tempo, velocidade e aceleração.

Aceleração? Sim, com efeito, o movimento circular uniforme é acelerado, mesmo quando sua velocidade v ser constante. Isso ocorre porque a velocidade v, Que é um vetor e é por isso que está em negrito, muda continuamente sua direção à medida que o objeto ou partícula gira. Qualquer mudança em v É produzido por uma aceleração que, como será vista, é direcionada para o centro da trajetória circular.

O movimento circular uniforme é um movimento no plano XY, Portanto, é um movimento bidimensional. No entanto, é possível expressá -lo de maneira mais confortável através do ângulo θ que varre a partícula, medido em relação ao eixo horizontal ou outro eixo de referência apropriado.

Mesmo que seja um objeto estendido, suas partículas sempre varrem o mesmo ângulo, mesmo que tenham coordenadas diferentes (X, y).

[TOC]

Características do movimento circular uniforme

Você pode resumir as características do movimento circular uniforme da seguinte forma:

-A trajetória é uma circunferência, portanto é um movimento no plano.

-A rapidez v É constante, mas a velocidade v Não, porque muda continuamente a direção e o significado para acomodar a curva do celular.

-O vetor de velocidade v É sempre tangencial à circunferência e perpendicular à direção radial.

-Velocidade angular ω é constante.

-Apesar de ser uniforme, há uma aceleração para explicar essas mudanças na direção da velocidade. Esta aceleração é a aceleração centrípeta.

-A aceleração centrípeta e a velocidade são perpendiculares entre si.

-É um movimento periódico ou repetitivo; portanto, o período e a frequência das magnitudes são definidas para ele.

Fórmulas de movimento circular uniforme

Neste esquema, há uma rotação de partículas P v retirou.

Pode servir a você: campo magnético da Terra: origem, características, função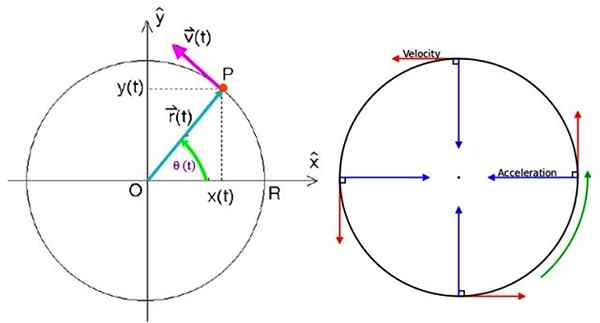 Parâmetros de movimento circular uniformes. Fonte: f. Zapata/Wikimedia Commons.

Para especificar o vetor de posição, é necessário.

Vetor de posição

É indicado como r (t) e é direcionado da origem para o ponto P onde a partícula está localizada. Em um instante, dado t, nas coordenadas cartesianas, está escrito como:

r (t) = x (t) Yo + e T) J

Onde Yo e J Eles são os vetores unitários perpendiculares nas direções x e e respectivamente. Do gráfico, observa -se que o módulo vetorial r (t) sempre bem R, O raio da circunferência. Se θ é o ângulo que se forma r Com o eixo horizontal, a posição também é igual a:

r (t) = [RCOS θ(t)] Yo +[Rsen θ(t)] J

O ângulo que se forma r (T) Com o eixo horizontal, é um ângulo central e seu valor é:

θ = s/r

Onde s é o arco de circunferência viajou e r o rádio. Disse ângulo θ É uma função de tempo, então você pode escrever θ = θ (T), chamar posição angular.

Como a velocidade é constante, a partícula descreve ângulos iguais em tempos iguais e em analogia com o movimento uniforme retilíneo, está escrito:

θ = θ (t) = θ_qualquer + ωt

Aqui θ_qualquer É o ângulo inicial medido em radianos em relação ao eixo de referência, pode ser 0 ou qualquer valor e ω é a velocidade angular.

Velocidade angular e velocidade linear

A velocidade angular é a primeira derivada da posição angular e é denotada como ω. Seu valor é constante para o movimento circular uniforme, uma vez que os ângulos iguais estão cercando em tempos iguais. Em outras palavras:

A velocidade angular vem em unidades de radianos/s. Por sua parte, a velocidade linear é calculada por:

A velocidade linear é o módulo ou magnitude da velocidade linear, que está mudando à medida que a partícula gira após sua trajetória. A direção da velocidade é, portanto, o endereço tangencial da circunferência.

As unidades da velocidade linear no movimento circular uniforme são as mesmas dos movimentos lineares: M/s (no sistema internacional SI), km/h, cm/s e outros.

Aceleração centrípeta

Na figura seguinte, há uma partícula que se move em um cronograma da circunferência com velocidade constante. Isso significa que o vetor de velocidade tem o mesmo módulo sempre, mas está mudando de direção para acomodar a circunferência.

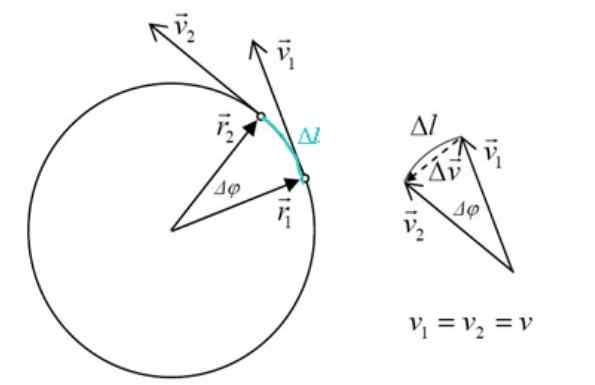Velocidade e aceleração no movimento circular uniforme. Fonte: f. Zapata.

Qualquer alteração na velocidade resulta em uma aceleração, que por definição é:

Pode atendê -lo: os 31 tipos de força na física e suas características

Na imagem acima está a subtração entre os vetores v₂ e v₁, cujo resultado é δv, vetor proporcional à aceleração. Como você pode ver, sempre aponta para o centro da circunferência e é por isso que é chamado de aceleração centrípeta ou aceleração radial.

O triângulo formado por v₂, v₁ e δv É semelhante ao triângulo lados r₂, r₁ e δeu, Sendo Δφ o ângulo central. As magnitudes de r₂ e r₁ Eles são iguais, então:

r₂ = r₁ = r

Então, de ambos os triângulos são esses relacionamentos para o ângulo:

Δφ = Δr / r; Δφ = ΔV / V

Não são necessários ousados, uma vez que a medida do ângulo depende das magnitudes desses vetores. Equalizando as expressões acima segue que:

 Então:

Dividindo de ambos os lados por Δt, para obter a magnitude da aceleração:

Mas Δr / Δt é a magnitude da velocidade, chamada v, portanto:

Finalmente, a aceleração centrípeta é:

Período e frequência

Como o movimento circular é repetitivo, o período é definido T do mesmo que o tempo que leva para o celular dar uma volta completa. Como o comprimento do raio do raio r é 2πr, o ângulo varrido em radianes quando se completa é 2π radianos e leva tempo t, a velocidade angular é:

Ω = 2π / t

T = 2π / ω

O período de movimento circular uniforme é medido em segundos no sistema internacional.

Por sua parte, a frequência F É o número de voltas por unidade de tempo e é o recíproco ou inverso do período:

F = n /t = 1 /t

A unidade de frequência no sistema internacional é S^-1.

Exemplos uniformes de movimento circular

Muitos objetos giram para produzir efeitos diversos: rodas, discos e turbinas. Uma vez atingido a velocidade de operação, a rotação geralmente é realizada com velocidade constante. O movimento circular é tão comum na vida cotidiana que você quase nunca pensa nisso, então aqui há alguns exemplos próximos que o ilustram muito bem:

Movimento da terra

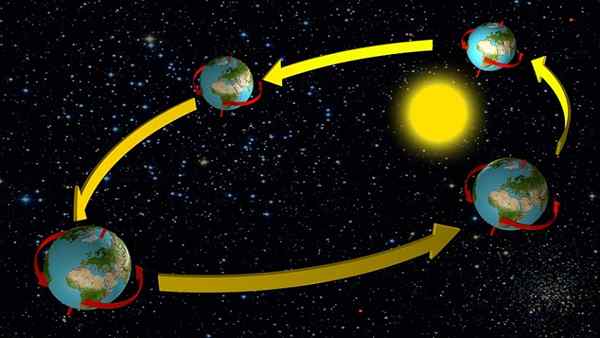
A Terra e outros planetas do sistema solar se movem em trajetórias elípticas de pequena excentricidade, exceto Mercúrio, o que significa que, na primeira abordagem, pode -se supor que seu movimento seja uniforme circular.

Isso tem uma boa idéia da velocidade da tradução ao redor do sol, pois no caso da Terra o período de movimento é conhecido: um ano ou 365 dias.

Partículas no limite de um álbum

As partículas que giram na beira de um antigo toadiscos ou a moda de um ventilador seguem um movimento circular uniforme, quando o dispositivo atingir sua velocidade de reprodução.

Pode atendê -lo: Dirac Jordan Atomic Model: características e postulações

telescópio espacial Hubble

O telescópio espacial Hubble gira em torno da Terra em aproximadamente 7550 m/s.

Centrífugadores

As máquinas de lavar realizam um processo centrifugado para espremer roupas, que consiste em girar o tambor de contêiner de alta velocidade. Os secadores também giram por um período de tempo com movimento circular uniforme.

A centrifugação também é usada em laboratórios para separar compostos, por exemplo, e, assim, separar seus constituintes por diferença nas densidades. Sempre que se fala em centrifugação, há um movimento circular que é uniforme, pelo menos por um tempo.

Chuveiros de jardim

Muitos chuveiros de jardim se transformam constantemente para a terra regar em um casal.

Esportes

No lançamento do martelo, por exemplo, que é uma disciplina olímpica, o atleta gira uma bola de metal com um cabo de aço preso à alça. O objetivo é enviar a bola o mais longe possível, mas sem deixar uma determinada área.

Exercício resolvido

Uma partícula se move em um círculo de raio de 2m com uma velocidade constante v = 8 m/s, na direção oposta ao relógio. Inicialmente a partícula estava em r = +2 J m. Calcular:

a) velocidade angular ω

b) sua posição angular θ (t)

c) o período de movimento

d) aceleração centrípeta.

e) posição da partícula após a passagem de t = π/4 s

Solução para

Da fórmula v = rΩ segue -se que:

Ω = v/r = (8 m/s)/2m = 4rad ∙ s^-1

Solução b

Tomando como eixo de referência para o eixo x positivo, a partícula é inicialmente a 90º = π/2 radianos em relação ao referido eixo, uma vez que a declaração diz que a posição inicial é +2 J M, isto é, a partícula está em y = 2m quando o movimento começa a seguir.

θ = θ (t) = θ_qualquer + ωt = π/2 + 4t

Solução c

T = 2π / ω = 2π / 4 s = 0.5 π s

Solução d

a = v² / R = (8 m/ s)² / 2 m = 32 m/ s²

Solução e

θ (t) = π/2 + 4t → θ (π/4) = π/2 + 4 ∙ (π/4) = 3π/2 radianos

Isso significa que depois desse tempo, a partícula está na posição y = -2m J. Faz sentido porque t = π/4 s é metade do período; portanto, a partícula visitou um ângulo de 180º em um sentido anti -marário, pois sua posição inicial e deve estar certa na posição oposta.

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
2. Giambattista, a. 2010. Física. 2º. Ed. McGraw Hill.
3. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1. Pearson.
4. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.
5. Zapata, f. Movimento circular. Recuperado de: Francesphysics.Blogspot.com.