Medição aproximada de figuras amorfas Exemplo e exercício

O Medição aproximada Das figuras amorfas consistem em uma série de métodos usados ​​para determinar a área ou perímetro de figuras geométricas que não são triângulos, quadrados, círculos, etc. Alguns são extensíveis a figuras tridimensionais.

Basicamente, a medição consiste em fazer um reticulado regularmente, como retângulos, quadrados ou trapézios, que cobrem aproximadamente a superfície. A precisão da abordagem da área obtida por esses métodos aumenta com a delicadeza ou densidade do reticulado.

figura 1. Pedras em forma de figuras amorfas. Fonte: Pxfuel.

As figuras 1 e 2 mostram várias figuras amorfas. Para calcular a área, um reticulado, composto por 2 x 2 quadrados, que por sua vez são subdivididos em vinte quadrados de 2/5 x 2/5.

Adicionando as áreas dos quadrados principais e os quadrados secundários A área aproximada da figura amorfa é obtida.

Figura 2. Um reticulado para calcular a área de uma das figuras amorfas de uma maneira aproximada. Fonte: f. Zapata

[TOC]

Área sob uma curva

É frequentemente necessário calcular a área sob uma curva entre dois valores limitados. Nesse caso, em vez de uma reticulada quadrada, listras retangulares podem ser rastreadas aproximadamente a área sob a referida curva.

A soma de todas as listras retangulares é chamada Soma ou soma de Riemann. A Figura 3 mostra uma partição do intervalo [a, b] no qual você deseja determinar aproximadamente a área sob a curva.

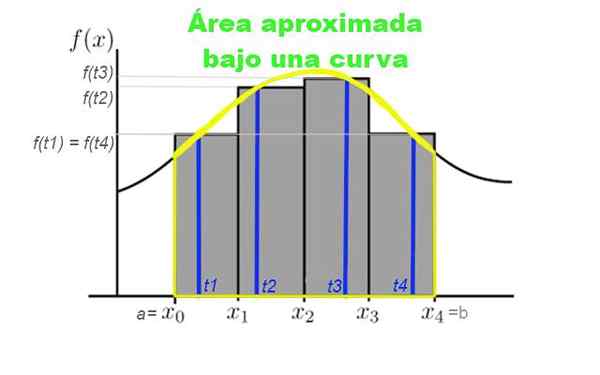Figura 3. Partição do intervalo [a, b] em quatro subintervalas, que geralmente são retirados da mesma largura. A altura dos retângulos é determinada pelo valor da curva para um TK pertencente aos subintervalos. Fonte: f. Zapata.

Suponha que você queira calcular a área sob a curva dada pela função y = f (x), onde x pertence ao intervalo [a, b] dentro do qual você deseja calcular a área. Para isso, é feita uma partição de n elementos nesse intervalo:

Pode atendê -lo: 60 divisores

Partition = x0 = a, x1, x2, ..., xn = b.

Então a área aproximada sob a curva dada por y = f (x) no intervalo [a, b] é alcançada pela seguinte quantia:

S = ∑_{K = 1}ⁿ f (t_k) (x_k - x_K-1)

Onde t_k está entre x_K-1 e x_k: x_K-1 ≤ t_k ≤ x_k .

A Figura 3 mostra a soma de Riemann da curva y = f (x) no intervalo [x0, x4]. Nesse caso, foi feita uma partição de quatro subintervalos e a soma representa a área total dos retângulos cinzentos. 

Esta soma representa uma abordagem para a área sob a curva f entre as abcissas x = x0 e x = x4.

A abordagem da área sob a curva melhora na medida em que o número n de partições é maior e tende a ser exatamente a área sob a curva quando o número n Partições tendem ao infinito. 

Caso a curva seja representada por uma função analítica, os valores f (t_k) Eles são calculados avaliando a referida função nos valores t_k. Mas se a curva não tiver uma expressão analítica, as seguintes possibilidades permanecem:

1. Abordar a curva por uma função, por exemplo, um polinômio.
2. Pegue as coordenadas cartesianas dos pontos em que a curva é interceptada com as linhas x = t_k.

Intervalos regulares

Dependendo da escolha do valor de TK no intervalo [X_k, x_K-1], a soma pode superestimar ou subestimar o valor exato da área sob a curva da função y = f (x). O mais aconselhável é levar o ponto TK em que a área ausente é aproximadamente igual à área restante, embora nem sempre seja possível fazer essa escolha.  

Pode servir a você: inverso multiplicativo: explicação, exemplos, exercícios resolvidos

Pegue o TK no final

O mais prático é usar intervalos regulares de amplo Δx = (b - a)/n, onde A e B são os valores mínimo e máximo da abcissa, enquanto n é o número de subdivisões.

Nesse caso, a área sob a curva se aproxima de:

Área = f (a+Δx)+f (a+2Δx)+…+f [a+(n-1] Δx+f (b)*Δx

Na expressão anterior, Tk foi levado na extremidade direita do subinterval.

Pegue o TK na extremidade esquerda

Outra possibilidade prática é assumir o valor da TK na extremidade esquerda; nesse caso, a soma que se aproxima da área é expressa como:

Área = [f (a)+f (a+Δx)+…+f (a+(n-1) Δx)*Δx

Tk como valor central

No caso de Tk ser escolhido como o valor central da subinterval regular da largura Δx, a soma que se aproxima da área sob a curva é:

Área = [f (a+Δx/2)+f (a+3Δx/2)+…+f (b- Δx/2)]*Δx

Qualquer uma dessas expressões tende ao valor exato na medida em que o número de subdivisões é arbitrariamente grande, isto é, que Δx tende a zero, mas neste caso o número de termos da soma é imensamente grande com o consequente custo computacional. 

Exemplo

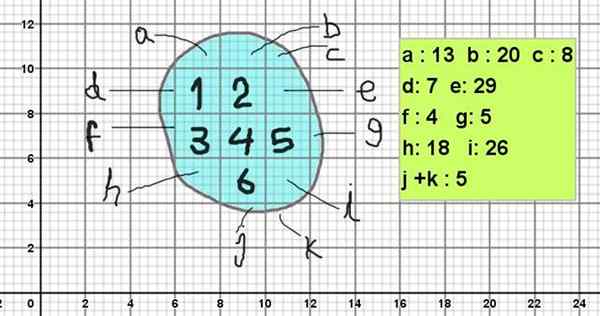
A Figura 2 mostra uma figura amorfa, cujo contorno é semelhante às pedras da imagem 1. Para calcular sua área, é colocada em um reticulado com quadrados principais de 2 x 2 unidades no quadrado (por exemplo, elas podem ser 2 cm²).

E como cada quadrado é subdividido em subdivisões de 5 x 5, cada subdivisão possui uma área de 0,4 x 0,4 unidades quadradas (0,16 cm²).

A figura da figura seria calculada da seguinte forma:

Pode atendê -lo: fatorização comum: exemplos e exercícios

Área = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

Quer dizer:

Área = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Exercício resolvido

Calcule aproximadamente a área sob a curva dada pela função f (x) = x² Aposta a = -2 até b = +2. Para fazer isso, escreva a soma para n partições regulares do intervalo [a, b] e depois tome o limite matemático para o caso de o número de partições tendem a infinito. 

Solução

Primeiro, o intervalo de partição é definido como 

Δx = (b - a)/n. 

Então a soma para a direita correspondente à função f (x) é assim:

A = -2 e b =+2 são substituídos para que o intervalo ou a etapa seja Δx = 4/n. Nesse caso, a soma para a função f (x) = x² é:

 O binomial quadrado é desenvolvido: 

[-2 +(4i/n)]² = 4 - 16 i /n + (4 /n)² Yo²

E então é substituído na soma:

Separando as sumões e tomando as quantidades constantes como um fator comum de cada soma é obtido:

 A primeira das soma, a segunda é:

E o terceiro é:

Substituindo a expressão da soma que você tem:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

Ao escolher um grande valor para N, você tem uma boa abordagem para a área sob a curva. No entanto, nesse caso, é possível alcançar o valor exato, levando o limite matemático quando N tende ao infinito:

Área = lim_{N-> ∞}[16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²]

Área = 16 - (64/2)+ (64/3) = 16/3 = 5,333.

Referências

1. Casteleiro, J. M. 2002. Cálculo abrangente (edição ilustrada). Madri: editorial ESIC.
2. Larson, r. 2010. Cálculo de uma variável. 9NA. Edição. McGraw Hill.
3. Purcell, e. 2007. Cálculo com geometria analítica. 9NA. Edição. Pearson Education.
4. Unican. História do conceito de integral. Recuperado de: repositório.Unican.é
5. UIs. Riemann somas. Recuperado de: matemática.UIs.Edu.co
6. Wikipedia. Área. Recuperado de: é.Wikipedia.com