Características da linha perpendicular, exemplos, exercícios

A linha perpendicular É aquele que forma um ângulo de 90º em relação a outra linha, curva ou superfície. Observe que quando duas linhas são perpendiculares e no mesmo plano, quando cortadas, elas formam quatro ângulos idênticos, cada um dos 90º.

Se um dos ângulos não for 90º, diz -se que as linhas são oblíquas. As linhas perpendiculares são frequentes em design, arquitetura e construção, por exemplo, a rede de tubos da imagem a seguir.

figura 1. Tubo reto de ângulo e numerosas linhas perpendiculares. Quantos ângulos de 90º podem ser contados nesta imagem? Fonte: piqsels.

A orientação das linhas perpendiculares pode ser diversa, como as mostradas abaixo:

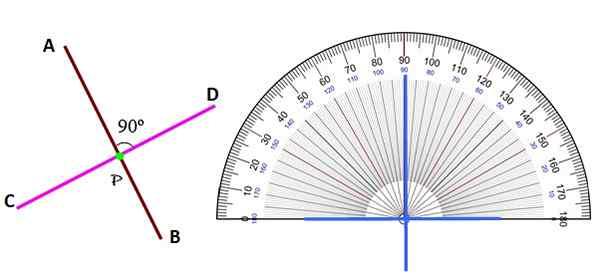
Figura 2. Linhas perpendiculares no avião. Fonte: f. Zapata.

Independentemente da posição, as linhas perpendiculares são reconhecidas pela identificação do ângulo entre elas como 90º, com a ajuda do transportador.

Observe que, diferentemente das linhas paralelas do plano, que nunca se cruzam, o perpendicular sempre o faz em um ponto P, chamado pé de uma das linhas na outra. Portanto, duas linhas perpendiculares também são Secantes.

Qualquer linha tem infinita perpendicular a ela, pois apenas deslocando o segmento AB para a esquerda ou direita no segmento de CD, teremos novos perpendiculares com outro pé.

No entanto, a perpendicular que passa apenas pelo ponto médio de um segmento é chamada bissetor do referido segmento.

[TOC]

Exemplos de linhas perpendiculares

Linhas perpendiculares são frequentes na paisagem urbana. Na imagem a seguir (Figura 3), apenas algumas das muitas linhas perpendiculares que são apreciadas na fachada simples deste edifício e em seus elementos como portas, dutos, etapas e mais: mais:

Pode atendê -lo: Fourier discreet transformado: propriedades, aplicações, exemplos Figura 3. Existem muitas linhas perpendiculares na fachada de um edifício comum como este. Fonte: Richard Kang através do Flickr.

O bom é que três linhas perpendiculares entre si ajudam -nos a estabelecer a localização dos pontos e objetos no espaço. Os eixos de coordenadas são identificados como X eixo, Eixo y e Z eixo, Claramente visível no canto de uma sala retangular como a seguinte:

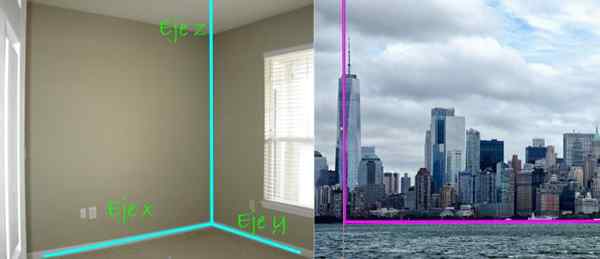Figura 4. O sistema de eixo cartesiano consiste em três linhas perpendiculares uma à outra, cada uma tem uma direção preferencial no espaço. Créditos da imagem esquerda: Treybunn 2 através do Flickr. Imagem direita; NeedPix.

Na vista panorâmica da cidade, à direita, a perpendicularidade entre os arranha -céus e o solo também é avisado. O primeiro diria que é encontrado em todo o Z eixo, Enquanto o solo é um avião, que neste caso é o plano XY.

Se o solo constituir o plano XY, O arranha -céu também é perpendicular a qualquer avenida ou rua, o que garante sua estabilidade, uma vez que uma estrutura inclinada é instável.

E nas ruas, onde quer que os cantos retangulares, existem linhas perpendiculares. Muitas avenidas e ruas têm um layout perpendicular, desde que a terra e os acidentes geográficos permitam.

Para expressar abruptamente a perpendicularidade entre linhas, segmentos ou vetores, o símbolo ⊥ é usado. Por exemplo, se a linha l₁ é perpendicular à linha L₂, nós escrevemos:

eu₁ ⊥ l₂

Mais exemplos de linhas perpendiculares

- No design, as linhas perpendiculares estão muito presentes, uma vez que muitos objetos comuns são baseados em quadrados e retângulos. Esses quadriláteros são caracterizados por ter 90 ângulos internos de 90º, porque seus lados são de dois a dois paralelos:

Pode servir a você: Equação Geral de Parábola (Exemplos e Exercícios)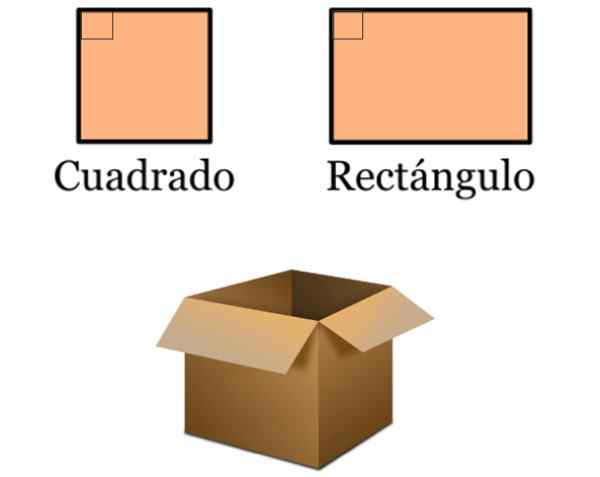 Figura 5. Quadrados e retângulos fazem parte de numerosos designs, como a desta caixa de papelão simples para armazenar mercadorias. Fonte: f. Zapata.

- Os tribunais nos quais diferentes esportes são praticados são demarcados por numerosos quadrados e retângulos. Estes, por sua vez, contêm linhas perpendiculares.

- Dois dos segmentos que compõem um triângulo retângulo são perpendiculares um ao outro. Estes são chamados categorias, enquanto a linha restante é chamada hipotenusa.

- As linhas de vetor de campo elétrico são perpendiculares à superfície de um equilíbrio eletrostático.

- Para um motorista carregado, o equipamento e o equipamento são sempre perpendiculares aos do campo elétrico.

- Em sistemas de tubos ou dutos usados ​​para transportar diferentes tipos de fluidos, como o gás que aparece na Figura 1, é comum para cotovelos em ângulos retos. Portanto, eles formam linhas perpendiculares, esse é o caso de uma sala de caldeira:

Figura 6. Tubos em uma sala de caldeira. Fonte: Wikimedia Commons. Roger McLlassus/CC BY-S (http: // criativeCommons.Org/licenças/BY-SA/3.0/)

Exercícios

- Exercício 1

Desenhe duas linhas perpendiculares por regra e bússola.

Solução

É muito simples de fazer, seguindo estas etapas:

-A primeira linha é desenhada, chamada ab (preta).

-Acima (ou abaixo se preferir) de AB Marks Point P, onde a perpendicular passará. Se P estiver logo acima (ou abaixo) metade de AB, a referida perpendicular é a bissetora do segmento AB.

-Com a bússola centrada em P, é desenhado um círculo que corta AB em dois pontos, chamados para 'e B' (vermelho).

Pode atendê -lo: números amigáveis ​​ou amigáveis: exemplos e como encontrá -los

-A bússola em A'P é aberta, ele se concentra em um círculo e um círculo que passa por P (verde).

-Repita a etapa anterior, mas agora abrindo a bússola o comprimento do segmento B'P (verde). Ambos os arcos de circunferência são cortados no ponto q abaixo de P e, claro, neste último.

-Os pontos P e Q são unidos à regra e a linha perpendicular (azul) já está pronta.

-Finalmente, todas as construções auxiliares devem ser cuidadosamente apagadas, deixando apenas perpendicularmente.

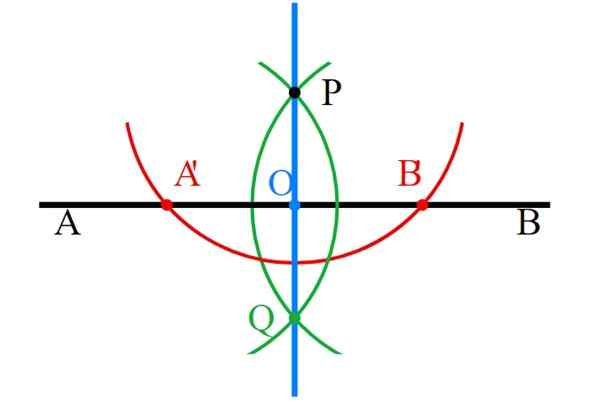Figura 6. Linhas percendulares com regra e compas. Fonte: Wikimedia Commons.

- Exercício 2

Duas linhas l₁ e eu₂ Eles são perpendiculares se suas respectivas inclinações m₁ e m₂ Eles cumprem esse relacionamento:

m₁ = -1/m₂

Dada a linha y = 5x - 2, encontre uma linha perpendicular a ela e passe pelo ponto (-1, 3).

Solução

-Primeiro de tudo é a inclinação da linha perpendicular M_⊥, Conforme indicado na declaração. A inclinação da linha original é m = 5, o coeficiente que acompanha "x". Então:

m_⊥= -1/5

-Então a equação da linha perpendicular é construída e_⊥, substituindo o valor encontrado anteriormente:

e_⊥= -1/5x + b

-Em seguida, o valor de B é determinado, com a ajuda do ponto dado pela declaração, o (-1,3), uma vez que a linha perpendicular deve passar por ela:

y = 3

x = -1

Substituindo:

3 = -1/5 (-1) + b

O valor de B é liberado:

B = 3- (1/5) = 14/5

-Finalmente a equação final é construída:

e_⊥= -1/5x + 14/5

Referências

1. Baldor, a. 2004. Geometria plana e espacial. Publicações culturais.
2. Clemens, s. 2001. Geometria com aplicações e resolução de problemas. Addison Wesley.
3. A matemática é divertida. Linhas perpendiculares. Recuperado de: Mathisfun.com.
4. Instituto Monterey. Linhas perpendiculares. Recuperado de: MontereyInstitute.org.
5. Wikipedia. Linhas perpendiculares. Recuperado de: é.Wikipedia.org.