Fermat limitá o que consiste e os exercícios resolvidos

Ele Limite Fermat É um método numérico usado para atingir o valor da inclinação de uma linha, que é tangente a uma função específica de seu domínio. Também é usado na obtenção de pontos críticos de uma função. Sua expressão é definida como:

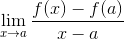
É óbvio que Fermat não sabia os fundamentos da derivação, no entanto, foram seus estudos que promoveram um grupo de matemáticos para perguntar sobre linhas tangentes e suas aplicações no cálculo.

[TOC]

Qual é o limite de Fermat?

Consiste em uma abordagem de 2 pontos, que em condições anteriores formam uma linha secante para a função com interseção em pares de valores.

Ao se aproximar da variável para o valor "A", o par de pontos é obrigado a atender. Dessa maneira, a linha de secagem anteriormente se torna tangente ao ponto (a; f (a)).

O valor do quociente (x - a), quando avaliado no ponto "A", lança uma indeterminação dos limites do tipo K entre zero (k/0). Onde essas indeterminações podem ser quebradas através de diferentes técnicas de fatorização.

As técnicas de operação mais usadas são:

-Diferença quadrada (um² - b² ) = (a + b) (a - b); A existência do elemento (a-b) implica em muitos casos o fator que simplifica a expressão (x-a) na razão de limite de fermat.

- Conclusão quadrada (machado² + bx); Depois de concluir os quadrados, é obtido um binomial de Newton, onde um de seus 2 fatores é simplificado com a expressão (x - a), quebrando a indeterminação.

- Conjugado (a + b) / (a ​​+ b); Multiplique e divida a expressão pelo conjugado de algum fator pode ser de grande ajuda para quebrar a indeterminação.

- Fator comum; Em muitos casos, o resultado da operação do numerador do Fermat f (x) - f (a) oculto ao fator (x - a) necessário para fatorar. Para isso, é observado cuidadosamente que elementos são repetidos em cada fator da expressão.

Fermat limite Aplicação para o máximo e o mínimo

Mesmo quando o limite de Fermat não diferencia o máximo e o mínimo.

O conhecimento básico sobre a teoria gráfica das funções em conutação com este teorema pode ser suficiente para estabelecer valores máximos e mínimos entre as funções. De fato, os pontos de inflexão podem ser definidos pelo teorema do valor médio adicional ao teorema de Fermat.

A parábola cúbica

O paradoxo mais significativo para Fermat veio ao estudar a parábola cúbica. Como sua atenção foi destinada às linhas tangentes de uma função para um determinado ponto, ele encontrou o problema de definir a referida linha tangente no ponto de inflexão existente na função.

Parecia impossível determinar a linha tangente a um ponto. Assim começa o inquérito que daria origem ao cálculo diferencial. Então definido por expoentes importantes da matemática.

Maximus e mínimo

O estudo do máximo e o mínimo de uma função foi um desafio para a matemática clássica, onde um método inequívoco e prático para a definição destes.

Fermat criou um método baseado na operação de pequenos valores diferenciais, que após os processos de fatoração são eliminados, dando lugar ao valor maior e mínimo.

Esta variável deve ser avaliada na expressão original para determinar a coordenada do referido ponto, que juntamente com os critérios analíticos será definido pelo máximo ou mínimo da expressão.

Método

Em seu método, Fermat usa o simbolismo literal de Vieta, que consistia no uso exclusivo de letras maiúsculas: as vogais, para as incógnitas e as consoantes para as quantidades conhecidas.

No caso de valores radicais, Fermat implementou um processo específico, que mais tarde seria usado nas fatizações dos limites da indeterminação Infinito entre o infinito.

Este processo consiste em dividir cada expressão pelo valor diferencial usado. No caso de Fermat, usou a letra e, onde após a divisão entre o maior poder de E, o valor procurado do ponto crítico se torna claro.

História

O limite de Fermat é de fato uma das contribuições menos conhecidas na longa lista do matemático. Seus estudos eram de números primos, para criar basicamente as bases para o cálculo.

Por sua vez, Fermat era conhecido por suas excentricidades em relação às suas hipóteses. Era comum um tipo de desafio para os outros matemáticos da época, quando ele já tinha a solução ou demonstração.

Tinha uma grande variedade de disputas e alianças com diferentes matemáticos da época, que amavam ou odiavam trabalhar com ele.

Seu último teorema foi o principal responsável por sua fama mundial, onde ele disse que uma generalização do Teorema de Pitágoras Para qualquer grau "n", era impossível. Disse ter uma demonstração válida, mas morreu antes de torná -lo público.

Esta demonstração teve que esperar aproximadamente 350 anos. Em 1995, os matemáticos Andrew Wiles e Richard Taylor terminaram a ansiedade deixada por Fermat, demonstrando que ele estava direto através de uma demonstração válida de seu último teorema.

Exercícios

Exercício 1

Defina a inclinação da linha tangente à curva f (x) = x² No ponto (4, 16)

Substituindo a expressão do limite de fermat que você tem:

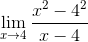
Em seguida, aplicando mínimos quadrados, o numerador é fator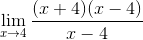

Os fatores são simplificados (x - 4)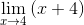

Ao avaliar você tem

M = 4 + 4 = 8

Exercício 2

Defina o ponto crítico da expressão f (x) = x² + 4x usando o limite de Fermat

Nesse caso, não há coordenadas, portanto o valor x é substituído pelo formulário genérico x₀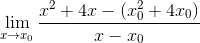

É realizado um agrupamento estratégico de elementos, buscando agrupar os colegas X-X₀

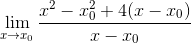
Quadrados são desenvolvidos

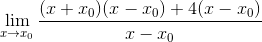
O fator comum X-X é observado_{0 e é extraído}

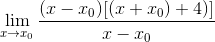
A expressão já pode ser simplificada e a indeterminação está quebrada

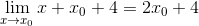
Nos pontos mínimos, sabe -se que a inclinação da linha tangente é igual a zero. Dessa forma, podemos corresponder a zero a expressão encontrada e limpar o valor x₀    

2 x₀ + 4 = 0

X₀ = -4/2 = -2

Para obter a coordenada ausente, você só precisa avaliar o ponto na função original

F (-2) = (-2)² + 4 (-2) = 4 - 8 = - 4

O ponto crítico é P (-2, -4).

Referências

1. Análise real. Uma abordagem histórica Sauhl Stahl, John Wiley & Sons, 5 de agosto. 1999.
2. A carreira matemática de Pierre por Fermat, 1601-1665: Segunda Edição. Michael Sean Mahoney. Princeton University Press, 5 de junho. 2018
3. De Fermat a Minkowski: Palestras sobre a teoria dos números e seu desenvolvimento histórico. C. Scharlau, h. Opolka, Springer Science & Business Media, 1985
4. Último Teorema de Fermat: Uma Introdução Genética à Teoria dos Números Algébricos. Harold m. Edwards. Springer Science & Business Media, 14 de janeiro. 2000
5. Fermat Days 85: Matemática para otimização. J.-B. Hiriart-uruty Elsevier, 1 de janeiro. 1986