Álgebra vetorial
- 1471
- 27
- Tim Mann
Qual é a álgebra vetorial?
Ele Álgebra vetorial É um ramo da matemática responsável pelo estudo de sistemas de equações lineares, vetores, matrizes, espaços vetoriais e suas transformações lineares. Está relacionado a áreas como engenharia, resolução de equações diferenciais, análise funcional, pesquisa de operações, gráficos computacionais, entre outros.
Outra das áreas que a álgebra linear adotou é a física, pois, por meio disso, foi possível desenvolver o estudo dos fenômenos físicos, descrevendo -os através do uso de vetores. Isso tornou possível uma melhor compreensão do universo.
Fundamentos
A álgebra vetorial se originou do estudo dos quaternions (extensão dos números reais) 1, i, j e k, bem como a geometria cartesiana promovida por Gibbs e Heaviside, que perceberam que os vetores serviriam como um instrumento para representar vários fenômenos físicos.
A álgebra vetorial é estudada através de três fundações:
Geometricamente
Os vetores são representados por linhas que têm uma orientação e operações como soma, subtração e multiplicação por números reais são definidos através de métodos geométricos.
Analiticamente
A descrição dos vetores e suas operações é realizada com números, chamados componentes. Este tipo de descrição é o resultado de uma representação geométrica porque um sistema de coordenadas é usado.
Axiomaticamente
Uma descrição dos vetores é feita, independentemente do sistema de coordenadas ou de qualquer tipo de representação geométrica.
O estudo das figuras no espaço é feito através de sua representação em um sistema de referência, que pode estar em uma ou mais dimensões. Entre os principais sistemas estão:
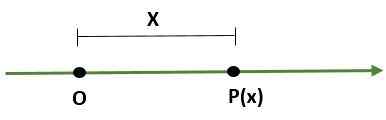
- Sistema unidimensional, que é uma linha em que um ponto (ou) representa a origem e outro ponto (p) determina a escala (comprimento) e a direção disso:

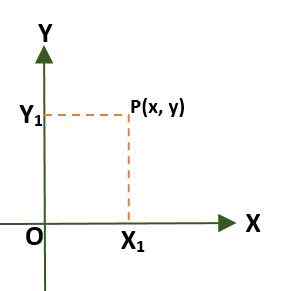
- Sistema de coordenadas retangulares (bidimensional), que é composto por duas linhas perpendiculares chamadas eixo x e y, que passam por uma origem (ou); Dessa maneira, o plano é dividido em quatro regiões chamadas quadrantes. Nesse caso, um ponto (P) no plano é dado pelas distâncias existentes entre os eixos e P.
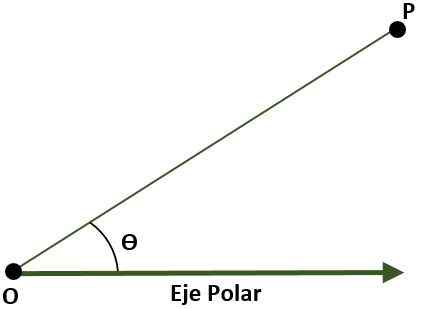
- Sistema de coordenadas polares (bidimensional). Nesse caso, o sistema é composto de um ponto O (origem) chamado polo e um semi -rio com origem ou eixo polar. Nesse caso, o ponto P do plano, com referência ao pólo e ao eixo polar, é dado pelo ângulo (ɵ), que é formado pela distância entre a origem e o ponto P.
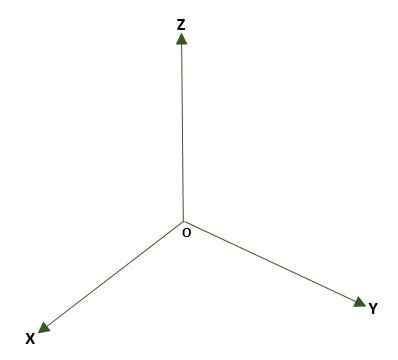
- Sistema tridimensional retangular, formado por três linhas perpendiculares (x, y, z) que têm como ponto ou no espaço. Três planos de coordenadas são formados: XY, XZ e YZ; O espaço será dividido em oito regiões chamadas octantes. A referência de um ponto P do espaço é dada pelas distâncias que existem entre os aviões e P.
Magnitudes
Uma magnitude é uma quantidade física que pode ser contada ou medida através de um valor numérico, como no caso de alguns fenômenos físicos; No entanto, muitas vezes é necessário descrever esses fenômenos com outros fatores que não são numéricos. É por isso que as magnitudes são classificadas em dois tipos:
Magnitude escalar
São aquelas quantidades definidas e representam de maneira numérica; isto é, por um módulo junto com uma unidade de medida. Por exemplo:
a) Tempo: 5 segundos.
b) Massa: 10 kg.
c) Volume: 40 ml.
d) Temperatura: 40 ºC.
Magnitude do vetor
São aquelas quantidades definidas e representadas por um módulo juntamente com uma unidade, bem como por um sentido e direção. Por exemplo:
Pode atendê -lo: simbolização de expressõesa) Velocidade: (5ȋ - 3ĵ) m/s.
b) Aceleração: 13 m /s2; S 45º e.
c) Força: 280 n, 120º.
d) Peso: -40 ĵ kg -f.
Magnitudes de vetor são representadas graficamente por vetores.
O que são vetores?
Os vetores são representações gráficas de uma magnitude vetorial; isto é, eles são segmentos de linha nos quais seu final final é a ponta de uma flecha.
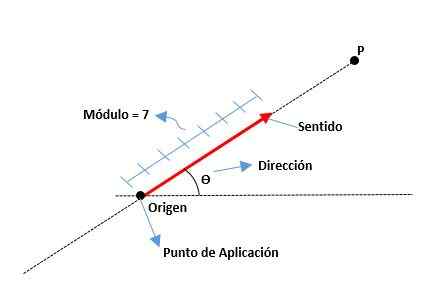
Estes são determinados por seu módulo ou comprimento do segmento, seu sentido que é indicado pela ponta de sua flecha e sua direção de acordo com a linha à qual pertence. A origem de um vetor também é conhecida como o ponto de aplicação.
Os elementos de um vetor são os seguintes:
Módulo
É a distância da origem até o final de um vetor, representado por um número real junto com uma unidade. Por exemplo:
| Om | = | A | = A = 6 cm
Endereço
É a medida do ângulo que existe entre o eixo x (do positivo) e o vetor, bem como os pontos cardinais (norte, sul, leste e oeste) também são usados.
Senso
É dado pela ponta da seta localizada no final do vetor, indicando onde isso é direcionado.
Classificação de vetores
Geralmente, os vetores são classificados como:
Vetor fixo
É aquele cujo ponto de aplicação (origem) é corrigido; isto é, ele permanece ligado a um espaço de espaço, para que não possa se mover neste.
Vetor livre
Pode se mover livremente no espaço porque sua origem se move para qualquer ponto sem alterar seu módulo, significado ou direção.
Vetor deslizante
É aquele que pode transferir sua origem ao longo de sua linha de ação sem alterar seu módulo, significado ou direção.
Propriedades vetoriais
Entre as principais propriedades dos vetores estão os seguintes:
Vetores de equipo
Eles são aqueles vetores livres que têm o mesmo módulo, direção (ou estes são paralelos) e sentido como um vetor deslizante ou um vetor fixo.
Vetores equivalentes
Ocorre quando dois vetores têm o mesmo endereço (ou são paralelos), o mesmo sentido e, apesar de terem módulos e pontos de aplicação diferentes, causam efeitos iguais.
Igualdade do vetor
Eles têm o mesmo módulo, direção e sentido, mesmo quando seus pontos de partida são diferentes, o que permite que um vetor paralelo se mova para si mesmo sem afetá -lo.
Vetores opostos
Eles são aqueles que têm o mesmo módulo e direção, mas seu significado é oposto.
Vetor unitário
É aquele em que o módulo é igual à unidade (1). Isso é obtido dividindo o vetor por seu módulo e é usado para determinar a direção e a direção de um vetor, no plano ou no espaço, usando os vetores de base ou unidade padronizados, que são:
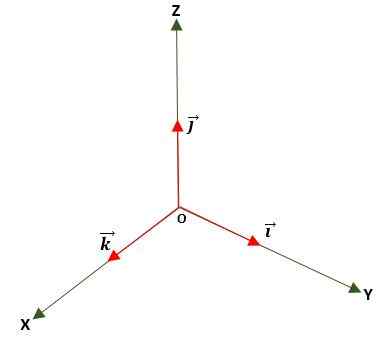
Vetor nulo
É aquele cujo módulo é igual a 0; isto é, seu ponto de origem e extremo coincidem no mesmo ponto.
Componentes vetoriais
Os componentes de um vetor são esses valores das projeções vetoriais nos eixos do sistema de referência; Dependendo da decomposição do vetor, que pode estar em eixos de duas ou três dimensões, dois ou três componentes serão obtidos, respectivamente.
Os componentes de um vetor são números reais, que podem ser positivos, negativos ou mesmo zero (0).
Dessa forma, se você possui um vetor ā, originário de um sistema de coordenadas retangulares no plano XY (bilimensional), a projeção no eixo X é āx e a projeção no eixo y e é āy. Assim, o vetor será expresso como a soma de seus vetores componentes.
Exemplos
Primeiro exemplo
Você tem um vetor ā que começa com a origem e as coordenadas de suas extremidades são dadas. Assim, o vetor ā = (āx; PARAe) = (4; 5) cm.
Pode atendê -lo: 120 divisores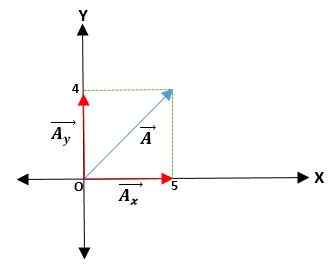
Se o vetor ā atuar na origem de um sistema de coordenadas triangulares tridimensionais (no espaço) x, y, z, para outro ponto (p), as projeções em seus eixos serão āx, āy e āz; Assim, o vetor será expresso como a soma de seus três vetores de componentes.
Segundo exemplo
Você tem um vetor ā que começa com a origem e as coordenadas de suas extremidades são dadas. Assim, o vetor ā = (ax; PARAe; PARAz) = (4; 6; -3) cm.
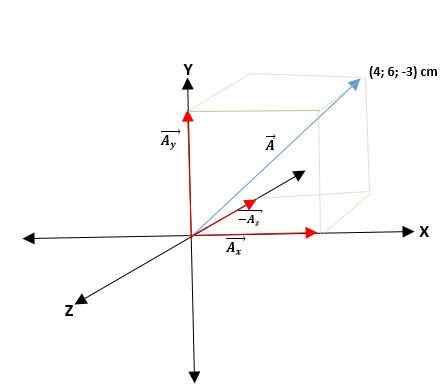
Os vetores que têm suas coordenadas retangulares podem ser expressas de acordo com seus vetores de base. Para isso, apenas cada coordenada deve ser multiplicada por seu respectivo vetor de unidade, de modo que, para o avião e o espaço, eles serão os seguintes:
Para o avião: ā = axi +aeJ.
Para o espaço: ā = axi +aeJ+azk.
Operações com vetores
Existem muitas magnitudes que têm módulo, significado e direção, como aceleração, velocidade, deslocamento, força, entre outros.
Eles são aplicados em várias áreas da ciência e, para aplicá -los, é necessário em alguns casos realizar operações como soma, subtração, multiplicação e divisão de vetores e escalares.
adição e subtração de vetores
A soma e a subtração de vetores são considerados uma única operação algébrica porque a subtração pode ser escrita como uma soma; Por exemplo, a subtração de vetores ā e ē pode ser expressa como:
Ā - ē = ā + (-ē)
Existem diferentes métodos para executar a soma e a subtração de vetores: eles podem ser gráficos ou análises.
Métodos gráficos
Usado quando um vetor tem um módulo, sentido e direção. Para isso, são desenhadas linhas que formam uma figura que posteriormente ajuda a determinar o resultante. Entre os mais conhecidos estão os seguintes:
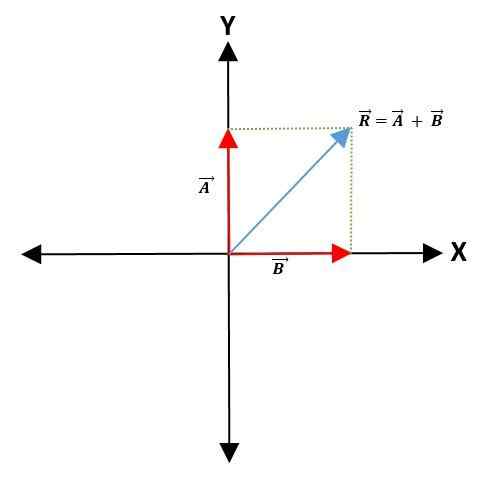
Método do paralelogramo
Para fazer a soma ou subtração de dois vetores, um ponto comum é escolhido no eixo de coordenadas -que representará o ponto de origem dos vetores -mantendo seu módulo, direção e direção.
Em seguida, linhas paralelas são atraídas para os vetores para formar um paralelogramo. O vetor resultante é a diagonal que sai do ponto de origem de ambos os vetores para o vértice do paralelogramo:
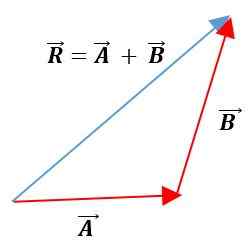
Método do Triângulo
Neste método, os vetores são colocados abaixo do outro, mantendo seus módulos, sentidos e endereços. O vetor resultante será a união da origem do primeiro vetor com o final do segundo vetor:
Métodos analíticos
Dois ou mais vetores podem ser adicionados ou subtraídos através de um método geométrico ou vetorial:
Método geométrico
Quando dois vetores formam um triângulo ou paralelogramo, o m [odulo e a direção do vetor resultante podem ser determinados usando as leis da mama e cosseno. Assim, o módulo vetorial resultante, aplicando a lei do cosseno e pelo método do triângulo, é dado por:
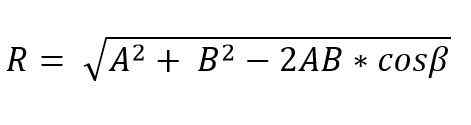
Nesta fórmula β é o ângulo oposto ao lado R, e isso é igual a 180º - ɵ.
Por outro lado, pelo método do paralelogramo, o módulo vetorial resultante é:
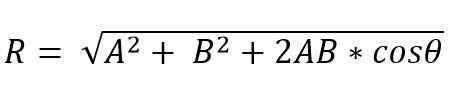
O endereço vetorial resultante é dado pelo ângulo (α), que forma o resultante com um dos vetores.
Por direito da mama, a soma ou subtração de vetores também pode ser feita pelo método do triângulo ou do paralelogramo, sabendo que em todos os triângulo os lados são proporcionais aos seios dos ângulos bonitos:
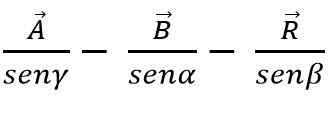
Método vetorial
Isso pode ser feito de duas maneiras: dependendo de suas coordenadas retangulares ou de seus vetores de base.
Os vetores que serão adicionados ou subtraídos à origem das coordenadas podem ser feitos, e todas as projeções são divididas em seus componentes retangulares em cada um dos eixos para o plano (x, y) ou espaço (x, x, e z); Finalmente, seus componentes são adicionados algebraicamente. Então, para o avião é:
Pode atendê -lo: números primos: características, exemplos, exercícios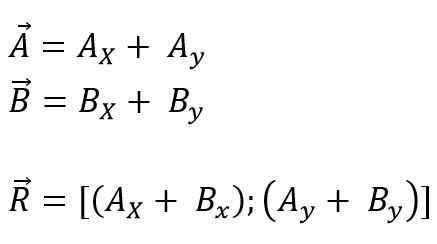
O módulo vetorial resultante é:
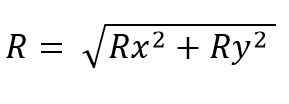
Enquanto para o espaço é:
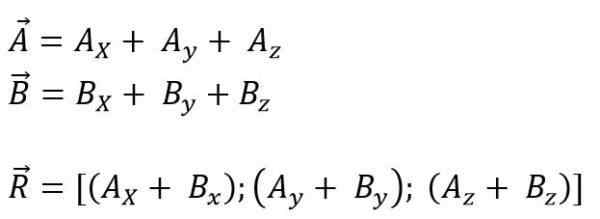
O módulo vetorial resultante é:
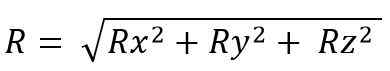
Quando as somas do vetor são realizadas, várias propriedades são aplicadas, que são:
- Propriedade associativa: O resultado não muda adicionando dois vetores primeiro e depois adicionando um terceiro vetor.
- Propriedade comutativa: A ordem dos vetores não altera o resultante.
- Propriedade distributiva vetorial: Se um escalar é multiplicado pela soma de dois vetores, é igual à multiplicação do escalar para cada vetor.
- Propriedade distributiva escalar: Se um vetor é multiplicado pela soma de dois escalares, é igual à multiplicação do vetor para cada escalar.
Multiplicação de vetores
A multiplicação ou produto dos vetores pode ser realizado como soma ou subtração, mas, ao fazê -lo, perde o significado físico e quase nunca está dentro das aplicações. Portanto, geralmente os tipos de produtos mais utilizados são o produto escalar e vetorial.
Produto escalar
Também é conhecido como um ponto de dois vetores. Quando os módulos de dois vetores são multiplicados pelo cosseno de ângulo menor que é formado entre eles, um escalar é obtido. Para expressar um produto escalar entre dois vetores, é colocado um ponto entre eles, e isso pode ser definido como:
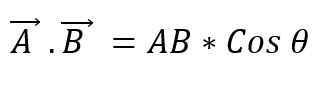
O valor do ângulo que existe entre os dois vetores dependerá se estes são paralelos ou perpendiculares; Assim, você tem que:
- Se os vetores forem paralelos e tiverem o mesmo sentido, Coseno 0º = 1.
- Se os vetores são paralelos e tiverem sentidos opostos, Coseno 180º = -1.
- Se os vetores forem perpendiculares, Coseno 90º = 0.
Esse ângulo também pode ser calculado sabendo disso:

O produto escalar tem as seguintes propriedades:
- Propriedade comutativa: a ordem dos vetores não altera o escalar.
- Propriedade distributiva: se um escalar for multiplicado pela soma de dois vetores, é igual à multiplicação de escalar para cada vetor.
Produto vetorial
A multiplicação de vetores, ou produto cruzado de dois vetores A e B, resultará em um novo vetor C e expressa usando um cruzamento entre os vetores:
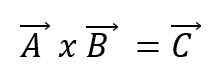
O novo vetor terá suas próprias características. Assim:
- O endereço: Este novo vetor será perpendicular ao plano, que é determinado pelos vetores originais.
- Ele senso: Isso é determinado com a regra da mão direita, onde o vetor a é transformado para o B apontando a direção da rotação com os dedos e, com o polegar, a direção do vetor está marcada.
- Ele módulo: É determinado pela multiplicação dos módulos dos vetores AXB, pelo seio do ângulo menor que existe entre esses vetores. É expresso:
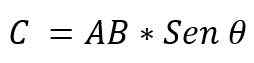
O valor do ângulo que existe entre os dois vetores dependerá se estes são paralelos ou perpendiculares. Portanto, é possível afirmar o seguinte:
- Se os vetores forem paralelos e tiverem o mesmo significado, seno 0º = 0.
- Se os vetores são paralelos e têm sentidos opostos, seno 180º = 0.
- Se os vetores forem perpendiculares, seno 90º = 1.
Quando um produto vetorial é expresso de acordo com seus vetores básicos, ele precisa:
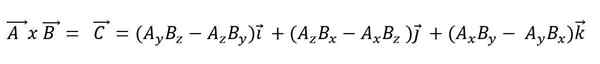
O produto escalar tem as seguintes propriedades:
- Não é comutativo: a ordem dos vetores altera o escalar.
- Propriedade distributiva: se um escalar for multiplicado pela soma de dois vetores, é igual à multiplicação de escalar para cada vetor.

