Bloquear elementos de álgebra, exemplos, exercícios resolvidos

Ele Álgebra de bloco Refere -se ao conjunto de operações que são executadas através de blocos. Esses e mais alguns elementos servem para representar esquematicamente um sistema e visualizar facilmente sua resposta a uma entrada específica.

Em geral, um sistema contém vários elementos elétricos, eletrônicos e eletromecânicos, e cada um deles, com sua respectiva função e posição no sistema, bem como a maneira como estão relacionados, é esquematizada por blocos funcionais.

figura 1.

Na figura acima, há um sistema muito simples, que consiste em um sinal de entrada X (s), que entra no bloco com a função de transferência G (s) que o modifica e produz a saída y (s).

É conveniente representar os sinais e sua jornada pelo sistema através de setas que entram e saem de cada bloco. Geralmente o fluxo de sinal é direcionado da esquerda para a direita.

A vantagem desse tipo de esquema é a ajuda visual que ele fornece para entender o sistema, embora não constitua uma representação física do mesmo. De fato, o diagrama de blocos não é único, porque de acordo com o ponto de vista, mesmo vários diagramas do mesmo sistema podem ser desenhados.

Também pode acontecer que o mesmo diagrama seja usado para vários sistemas que não estão necessariamente relacionados entre si, desde que seu comportamento descreva corretamente. Existem diferentes sistemas cuja resposta é semelhante em muitos aspectos, por exemplo, um circuito LC (canal indutor) e um sistema de resort de massa.

[TOC]

O que é um diagrama de blocos?

Os sistemas geralmente são mais complicados do que os da Figura 1, mas a álgebra de bloco fornece uma série de regras simples para manipular o esquema do sistema e reduzi -lo à sua versão mais simples.

Conforme explicado no início, o diagrama usa blocos, setas e círculos para estabelecer a relação entre cada componente do sistema e o fluxo dos sinais que passam por ele.

A álgebra de bloco permite comparar dois ou mais sinais através da soma, subtração e multiplicação deles, além de analisar a contribuição que cada componente faz com o sistema.

Graças a isso, é possível reduzir todo o sistema a um único sinal de entrada, uma função de transferência exclusiva que descreve completamente a ação do sistema e a saída correspondente.

Pode atendê -lo: astroclymias: história, que estudos, ramificações

Elementos do diagrama de bloco

Os elementos do diagrama de blocos são os seguintes:

O sinal

Os sinais são muito variados, por exemplo, é comum ser uma corrente elétrica ou uma tensão, mas pode ser brilhante, som e mais. O importante é que ele contém informações sobre um determinado sistema.

O sinal é indicado com uma letra maiúscula se for uma função da variável s da transformação de Laplace: x (s) (veja a Figura 1) ou com minúsculas se for baseado no tempo t, como x (t).

No diagrama de blocos, o sinal de entrada é representado por uma seta direcionada para o bloco, enquanto o sinal de saída, indicado como y (s) ou (t), é indicado com uma flecha de saída.

O sinal de entrada e saída é único e o endereço no qual os fluxos de informação são determinados pela direção da seta. E álgebra é a mesma para qualquer uma das duas variáveis.

O bloco

O bloco é representado por um quadrado ou um retângulo (consulte a Figura 1) e pode ser usado para realizar operações ou implementar a função de transferência, que geralmente é indicada com a letra maiúscula G. Esta função é um modelo matemático pelo qual a resposta oferecida pelo sistema é descrita antes de um sinal de entrada.

A função de transferência pode ser expressa em termos de tempo t como g (t) ou a variável s como g (s).

Quando o sinal de entrada X (s) chega ao bloco, ele é multiplicado pela função de transferência e se transforma no sinal (s) de saída y (s). Matematicamente, é expresso da seguinte maneira:

E (s) = x (s).G (s)

Da mesma forma, a função de transferência é a razão entre a transformação de Laplace do sinal de saída e a transformação de Laplace do sinal de entrada, desde que as condições iniciais do sistema sejam nulas:

G (s) = y (s) / x (s)

Ponto de soma

A soma ou verão é simbolizada por um círculo com uma cruz dentro. É usado para combinar, por somas e subtração, dois ou mais sinais. No final da seta que simboliza o sinal, um sinal + é colocado diretamente se esse sinal for adicionado ou um sinal - se subtraído.

Na figura a seguir, há um exemplo de como o verão funciona: você tem o sinal de entrada x, ao qual os sinais A e B são adicionados, obtendo como resultado a saída e, que é igual a algebraicamente:

Pode servir a você: Tiro vertical: fórmulas, equações, exemplos

Y = x+a+b

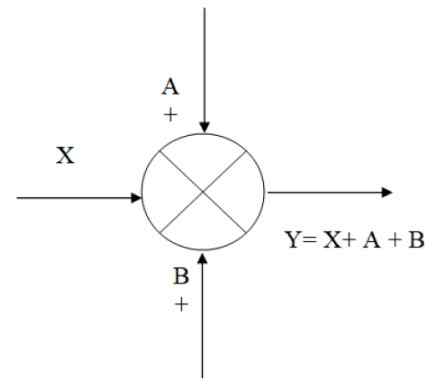Figura 2. Exemplo de uma aplicação. Fonte: f. Zapata.

Ponto de ramificação

Também é chamado Ponto de bifurcação. Nele, o sinal que sai de um bloco é distribuído a outros blocos ou a uma pluma. É representado por um ponto colocado na seta do sinal e outra flecha vem dele que redireciona o sinal em direção a outra parte.

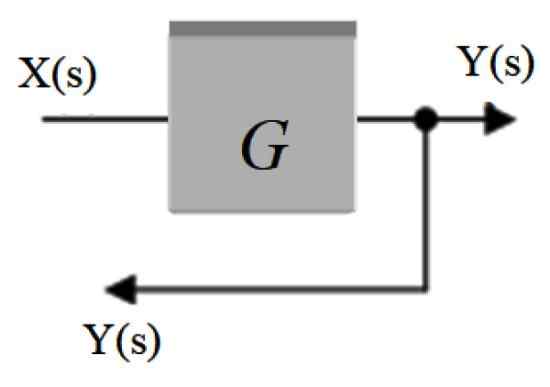Figura 3. Ponto de ramificação. Fonte: f. Zapata.

Exemplos de blocos da álgebra de bloco

Como explicado anteriormente, a idéia é expressar o sistema através do diagrama de blocos e reduzi -lo para encontrar a função de transferência que o descreve. A seguir, são apresentadas as regras da álgebra de bloco para simplificar os diagramas:

Blocos em cascata

Quando você tem um sinal que passa sucessivamente pelos blocos G₁, G₂, G₃..., é reduzido a um bloco único cuja função de transferência é o produto de G₁, G₂, G₃..

No exemplo a seguir, o sinal X (s) entra no primeiro bloco e sua saída é:

E₁(s) = x (s).G₁(S)

Figura 4. Dois blocos em cachoeira. Fonte: f. Zapata.

Por sua vez e₁(s) insira o bloco G₂(s), cuja partida é:

E₂(s) = x (s).G₁(S). G₂(S)

O procedimento é válido para n blocos de cascata:

E_n (s) = x (s). G₁(S).G₂(S) ... g_n(S)

Blocos em paralelo

No diagrama esquerdo, o sinal X (s) bifurca para entrar nos blocos G₁(S) e g₂(S):

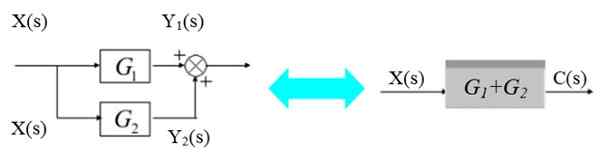Figura 5. Dois blocos em paralelo. Fonte: f. Zapata.

Os respectivos sinais de saída são:

E₁(s) = x (s).G₁(S)

E₂(s) = x (s).G₂(S)

Esses sinais são adicionados para obter:

C (s) = Y₁(s) +₂(s) = x (s).[G₁(s) + g₂(s)]

Como mostrado no diagrama direito.

Mova um pretendente para a esquerda

Um verão pode se mudar para a esquerda do bloco da seguinte maneira:

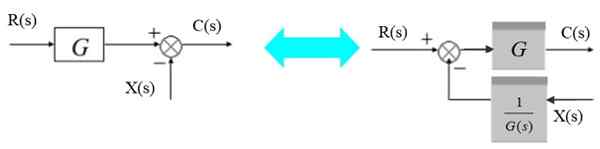Figura 6. Mova o adidor à esquerda do bloco. Fonte: f. Zapata.

À esquerda, o sinal de saída está:

C (s) = r (s). G (s) - x (s)

Equivalentemente para a direita:

C (s) = [r (s) - x (s)/g (s)]].G (s)

Mova uma direita para a direita

O verão pode se mover para a direita do bloco como este:

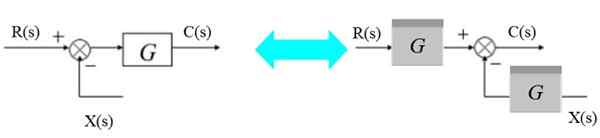Figura 7. Mova um enredo para a direita do bloco. Fonte: f. Zapata.

À esquerda, você tem: [r (s) - x (s)].G (s) = c (s)

Pode servir a você: Princípio de Arquimedes: Fórmula, Demonstração, Aplicações

E para a direita:

R (s). G (s) - x (s).G (s) = c (s)

Mova um ponto de bifurcação da esquerda para a direita

Para deslocar o ponto de bifurcação da esquerda para a direita do bloco, é suficiente observar que a saída C (s) à direita é o produto X (s).G (s). Como você deseja se tornar x (s) novamente, é multiplicado pelo inverso de g (s).

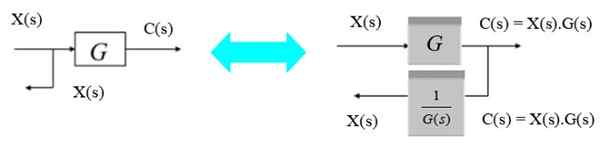Figura 8. Mova um ponto de ramificação da esquerda para a direita. Fonte: f. Zapata.

Mover um ponto de bifurcação da direita para a esquerda

Como alternativa, o ponto de bifurcação pode se mover da direita para a esquerda da seguinte maneira:

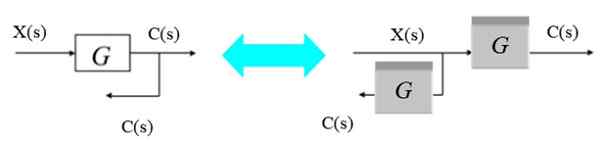Figura 9. Mova um ponto de ramificação da direita para a esquerda. Fonte: f. Zapata.

Como a saída da bifurcação deseja obter C (s), um novo bloco G (s) é simplesmente intercalado em um ponto de bifurcação à esquerda do bloco original.

Sistema com feedback

No sistema a seguir, o sinal de saída C (s) é alimentado através do submisso à esquerda:

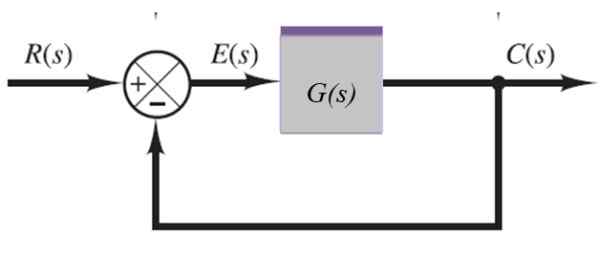Figura 10. Sistema com feedback. Fonte: f. Zapata.

C (s) = e (s).G (s)

Mas:

E (s) = r (s) -c (s)

Substituir essa expressão na equação anterior é: c (s) = [r (s) -c (s)]].G (s), do qual C (s) pode ser liberado:

C (s) + C (s).G (s) = r (s).G (s) → C (s). [1 + g (s)] = r (s).G (s)

C (s) = r (s).G (s) / [1 + g (s)]

Ou alternadamente:

C (s) / r (s) = g (s) / [1 + g (s)]]

Graficamente, depois de simplificar, é:

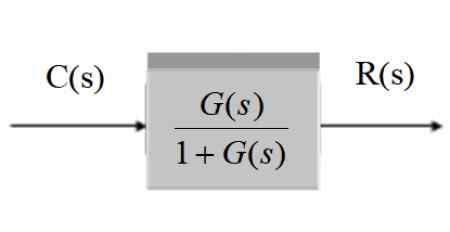Figura 11. Simplificação de um sistema com feedback. Fonte: f. Zapata.

Sistema com feedback e transdutor

O transdutor consiste na função de transferência h (s):

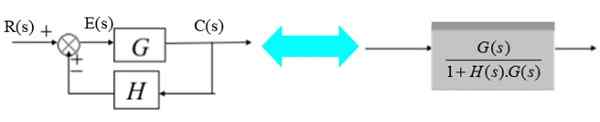Figura 12. Sistema com feedback e transdutor. Fonte: f. Zapata.

No diagrama certo, o sinal de saída C (s) é:

C (s) = e (s). G (s) com e (s) = r (s) - c (s).H (s)

Então:

C (s) = [r (s) - c (s). H (s)]. G (s)

C (s) [1+ h (s).G (s)] = r (s).G (s)

Portanto, C (s) pode ser limpo por:

C (s) = g (s).R (s) / [1+ h (s).G (s)]

E a função de transferência será:

G (s) / [1+ h (s).G (s)]

Como mostrado no diagrama direto simplificado.

Exercícios resolvidos

Exercício 1

Encontre a função de transferência do seguinte sistema:

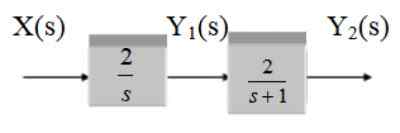Figura 13. Sistema de dois blocos em cascata. Fonte: f. Zapata.

Solução

São dois blocos em cascata, portanto a função de transferência é o produto das funções G₁ e g₂.

Se tem que:

G₁ = 2/s

G₂ = 2 /(s+1)

Portanto, a função de transferência procurada é:

G (s) = 4 / [s (s+1)]

Exercício 2

Reduza o seguinte sistema:

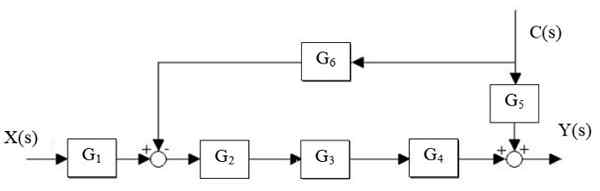Figura 14. Simplificação de um sistema. Fonte: f. Zapata.

Solução

Primeiro a cascata G é reduzida₂, G₃ e g_4, E o par paralelo é separado₅ e g₆:

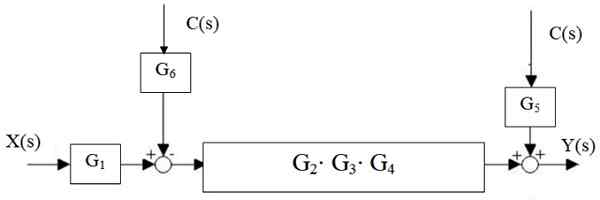Figura 15. Redução em cascata central. Fonte: f. Zapata.

Então, o pretendente à esquerda do bloco G₂ ⋅g₃ ⋅ g₄ Ele se move para a direita:

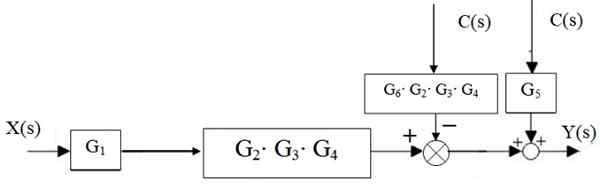Figura 16. Transferência do administrador. Fonte: f. Zapata.

Os verões da direita são reduzidos a um, bem como os blocos de Cascade:

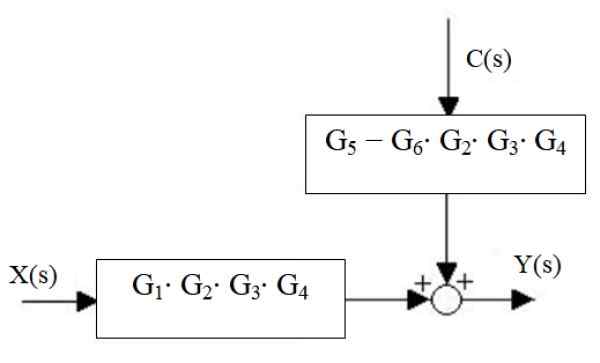Figura 17. Redução da nova cachoeira e os verões do direito. Fonte: f. Zapata.

Finalmente, a saída do sistema é:

E (s) = x (s) ⋅g₁⋅ g₂ ⋅g₃ ⋅ g₄ + C (s) ⋅ [g₅ - G₆ ⋅ g₂ ⋅g₃ ⋅ g₄]

Referências

1. Alaydi, J. Controle do diagrama de blocos do sistema. Recuperado de: site.iugaza.Edu.$.
2. Bolton, w. 2006. Engenharia de Controle. 2º. Edição. Alfa Ômega.
3. Cwalinsky, J. Introdução à Álgebra de Bloco do Sistema. Recuperado de: cedengerendo.com.
4. DademuchConnection. Bloqueia o diagrama. Recuperado de: Dademuch.com.
5. Ogata, k. 2010. Engenharia de controle moderno. 5 ª. Edição. Pearson.