Lei de Kirchhoff

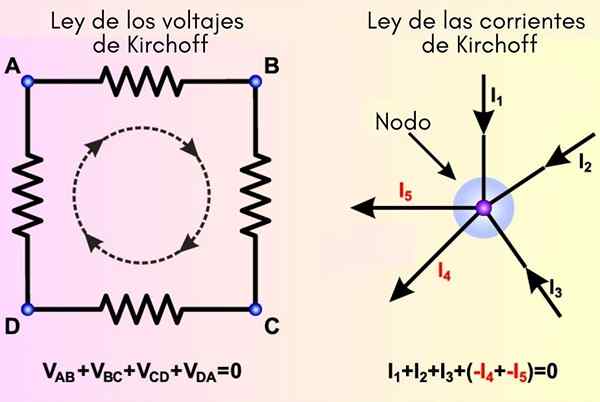
As leis de Kirchoff derivam dos princípios de energia e conservação de carga, respectivamente. À esquerda, a lei das malhas é estabelecida e à direita as correntes

Quais são as leis de Kirchoff?

As Lei de Kirchoff Eles consistem em aplicar o princípio de conservação da carga elétrica e o princípio da conservação de energia aos circuitos elétricos, a fim de resolver aqueles que têm várias malhas.

Essas regras, como não são leis no sentido estrito, são devidas ao físico alemão Gustav Kirchoff (1824-1887). Seu uso é essencial quando a lei de Ohm não é suficiente para determinar tensões e correntes no circuito.

Antes da declaração e aplicação das leis de Kirchoff, é conveniente lembrar o significado de alguns conceitos importantes sobre circuitos elétricos:

• Nó: Ponto de união entre dois ou mais fios condutores.
• Filial: Elementos do circuito que estão entre dois nós consecutivos, através dos quais a mesma corrente circula.
• Malha: Trajetória ou circuito fechado composto por dois ou mais galhos e que são percorridos na mesma direção, sem passar pelo mesmo ponto.

Primeira lei de Kirchoff

Também é conhecido como a lei das correntes ou regra dos nós e estabelece que:

A soma das correntes que entra em um nó é igual à soma das correntes que saem dela.

Então, de maneira matemática, a primeira lei é expressa como:

∑ i = 0

Onde o símbolo σ indica uma soma.

A equação anterior estabelece que, como a carga elétrica não é criada ou destruída, toda a corrente (carga por unidade de tempo) que entra no nó deve ser igual àquele que sai dele.

Pode atendê -lo: satélites artificiais

Exemplo

Para aplicar convenientemente a lei das correntes, um sinal é atribuído às correntes de entrada e o sinal oposto às correntes de saída. A escolha é completamente arbitrária.

A imagem a seguir mostra duas correntes que entram em um nó, desenhado em vermelho: i₁ e eu₂, e que, ao sair, eles são mostrados em verde: as correntes i₃, Yo₄ e eu₅.

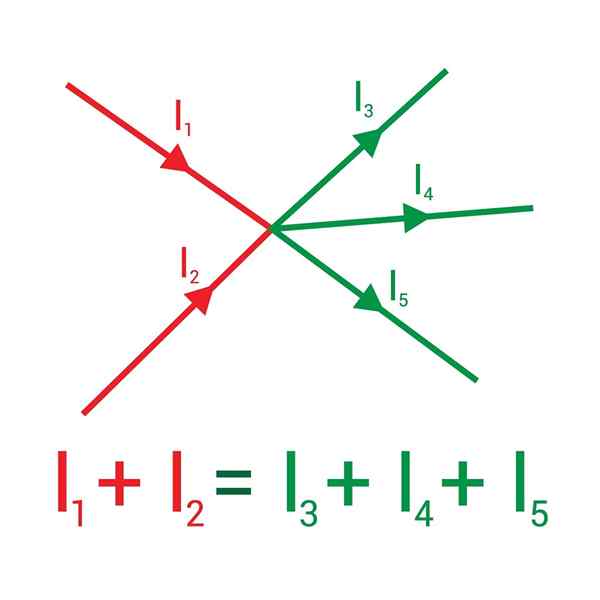A soma das correntes que entram em um nó é igual à soma das correntes que saem dela

Atribuindo o sinal (+) às correntes de entrada e ao (-) à saída, a primeira regra de Kirchoff estabelece que:

Yo₁ + Yo₂ - Yo₃ - Yo₄ - Yo₅= 0 ⇒ eu₁ + Yo₂ = I₃ + Yo₄ + Yo₅

Segunda Lei de Kirchoff

Outros nomes da segunda lei de Kirchoff são: Lei de tensões, Lei de tensões qualquer Lei da malha. De qualquer forma, estabelece que:

A soma algébrica de gotas de tensão ao longo de uma malha é igual a 0.

Essa é uma maneira de aplicar a conservação de energia no circuito, uma vez que a tensão em cada elemento é a mudança de energia por unidade de carga.

Portanto, ao viajar uma parte fechada (uma malha), a soma algébrica da tensão aumenta e as quedas são 0 e podem ser escritas:

∑ V = 0

Exemplo

Na figura seguinte, você tem a malha ABCDA, através da qual uma corrente circula na direção das agulhas do relógio e a rota pode começar em qualquer ponto do circuito.

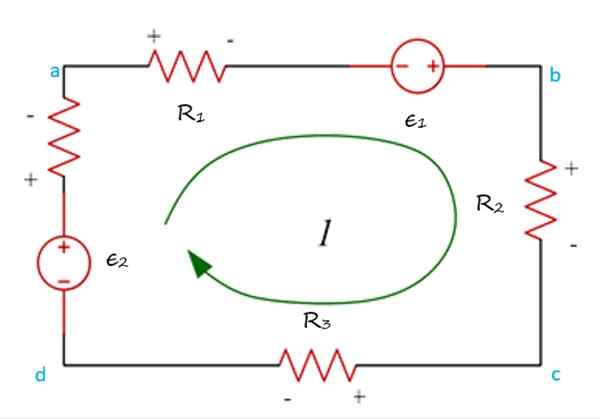Exemplo de uma malha visitada em um cronograma, onde os aumentos e as quedas potenciais são mostrados para aplicar a lei de tensões de Kirchoff. Fonte: f. Zapata.

Também é necessário. O habitual é atribuir como positivo o aumento da tensão, ou seja, quando a corrente circula de ( -) para (+). Então, a queda de tensão, que ocorre quando a corrente vai de (+) a ( -), é negativa.

Pode atendê -lo: óxido de silício (SiO2): estrutura, propriedades, usos, obtenção

Iniciar a rota de malha no ponto "A", é a resistência r₁. Nele, as cargas experimentam uma queda potencial, simbolizada pelos sinais (+) à esquerda e ( -) acima da resistência.

Portanto, a tensão ou tensão em R₁ Tem um sinal negativo.

Então você atinge uma fonte de tensão direta, chamada ε₁, cuja polaridade é menor (-) Mais (+). Lá as cargas elétricas passam por um aumento potencial e essa fonte é considerada positiva.

Seguindo este procedimento para a resistência restante e a outra fonte, a seguinte equação é obtida como resultado:

−v₁ + ε₁ - V₂ - V₃ + ε₂ = 0

Onde V₁, V₂ e V₃ são tensões em resistências r₁, R₂ e r₃. Essas tensões podem ser encontradas na lei de Ohm: v = i · r.

Exercício resolvido

Encontre o valor das correntes i₁, Yo₂ e eu₃ mostrado na figura.

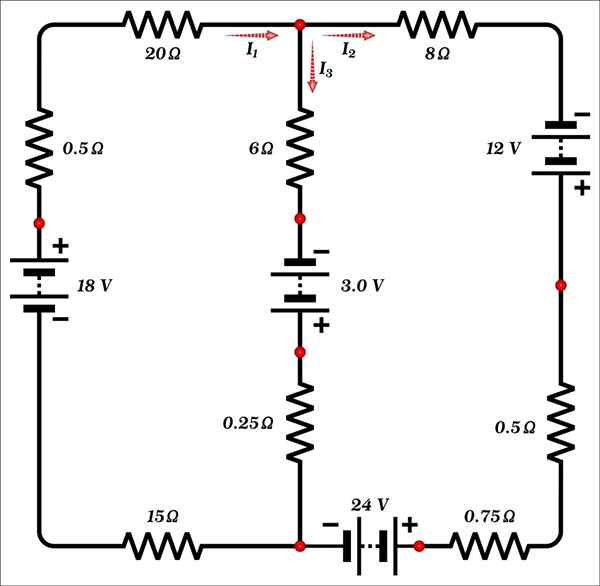
Solução

Este circuito consiste apenas em duas malhas e tem 3 incógnitas: as correntes e₁, Yo₂ e eu₃, Portanto, pelo menos três equações são necessárias para encontrar a solução.

No nó (ponto marcado em vermelho) que está no topo do circuito no ramo central, observa -se que a corrente i₁ está chegando, enquanto as correntes i₂ e eu₃ Eles são extrovertidos.

Portanto, a Lei das Correntes Kirchoff leva à primeira equação:

1) i₁ - eu₂ - eu₃ = 0

O nó inferior fornece as mesmas informações, portanto, o próximo passo é viajar pelas malhas.

Primeira malha

Para estabelecer a seguinte equação, a malha à esquerda é percorrida em um cronograma, a partir do canto superior esquerdo. Este é o sentido em que as correntes e correntes circulam₁ e eu₃.

Pode atendê -lo: comparador óptico: para que serve e peças

Observe que:

• Yo₁ passa pelas resistências de 20 Ω, 15 Ω e 0.5 Ω e a bateria de 18 V, onde ele experimenta um aumento potencial.
• Por sua parte, eu₃ Atravessa as resistências do ramo central de 6 Ω e 0.15 Ω e na bateria 3.0 V é um aumento potencial.

Da mesma forma, a lei ohm v = i ∙ r é usada para estabelecer a tensão em cada resistência, de acordo com isso:

-20 ∙ i₁ - 6 ∙ I₃ + 3.0 - 0.25 ∙ i₃ -15 ∙ i₁ + 18.0 - 0.5 ∙ i₁ = 0

Pedindo os termos:

(-20 −15 - 0.5) ∙ I₁ - (6 + 0.25) ∙ I₃  = - 3.0 - 18.0

-35.5 ∙ i₁ - 6.25 ∙ i₃ = - 21.0

2) 5 ∙ I₁ + 6.25 ∙ i₃ = 21.0

Segunda malha

A terceira equação é obtida em turnê pela malha à direita, começando no nó do topo do circuito. Observa -se que:

• Yo₂ Passar pelas resistências de 8 Ω, 0.5 Ω e 0.75 Ω, mais 12 V e 24 V baterias. De acordo com a polaridade das baterias, na rota há um aumento no potencial nos 12 V e diminuição dos 24 V.
• Importante: O passeio da segunda malha (em um cronograma) se opõe a eu₃, Portanto, as tensões nas resistências de 6 Ω e 0.25 Ω são aumentos potenciais e carregam um sinal positivo. De acordo com a polaridade das baterias, há um aumento nos 12 V e cair naqueles de 24 V e 3 V.

Com tudo isso, você chega:

-8 ∙ i₂ - 0.5 ∙ i₂ - 0.75 ∙ i₂ + 12.0 - 24.0 + 0.25 ∙ i₃ - 3.0 + 6 ∙ I₃ = 0

3) -25 ∙ i₂ + 6.25 ∙ i₃ = 15.0

Cálculo atual

Equações 1), 2) e 3) formam um sistema de 3 equações lineares com 3 incógnitas, cuja solução é:

Yo₁ = 0.381 a; Yo₂ = -0.814 A; Yo₃ = 1.195 a

O sinal negativo na corrente i₂ significa que ele flui na direção oposta do esquema.