Leis de Kepler Explicação, Exercícios, Experimento

As Leis de Kepler Sobre o movimento planetário foi formulado pelo astrônomo alemão Johannes Kepler (1571-1630). Kepler os deduziu com base no trabalho de seu professor dinamarquês Tycho Brahe (1546-1601).

Brahe compilou cuidadosamente os dados dos movimentos planetários por mais de 20 anos, com precisão e precisão surpreendentes, se for levado em consideração que no momento em que o telescópio ainda não havia sido inventado. A validade dos seus dados ainda é válida hoje.

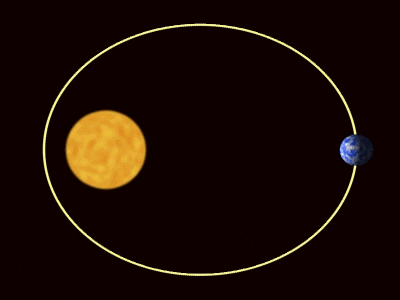figura 1. As órbitas dos planetas de acordo com as leis de Kepler. Fonte: Wikimedia Commons. Willow/CC por (https: // CreativeCommons.Org/licenças/por/3.0)

[TOC]

3 leis de Kepler

As leis de Kepler estabelecem:

-Primeira lei: Todos os planetas descrevem órbitas elípticas com o sol em um dos holofotes.

-Segunda lei ou lei da mesma: Uma linha direcionada do sol para qualquer planeta (rádio focal), varre áreas iguais em tempos iguais.

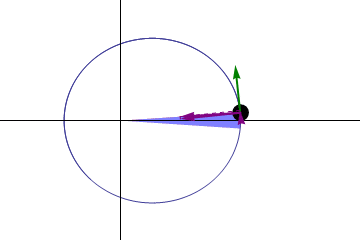Figura 2. Lei das áreas. Fonte: Wikimedia Commons. Gonfer/CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0)

-Terceira lei: O quadrado do tempo que leva qualquer planeta orbital ao redor do sol é proporcional ao cubo de sua distância média do sol.

Ser T disse o tempo chamado Período orbital, e r A distância média, então:

T² é proporcional a r³

T = k r³

Isso significa que o quociente T²/ r³ É o mesmo para todos os planetas, o que torna possível calcular o raio orbital, se o período orbital for conhecido.

Quando T É expresso em anos e r Nas unidades astronômicas ua*, a constante de proporcionalidade vale k = 1:

T²= r³

*Uma unidade astronômica é equivalente a 150 milhões de quilômetros, que é a distância média entre a Terra e o Sol. O período orbital da Terra é de 1 ano.

A Lei da Gravitação Universal e a terceira lei de Kepler

A Lei da Gravitação Universal estabelece que a magnitude da força de atração gravitacional entre dois objetos de massa M e m respectivamente, cujos centros estão separados a uma distância r, É dado por:

F = g mm /r²

G é a constante de gravitação universal e seu valor é g = 6.674 x 10 ^-onze N.m²/kg² .

Agora, as órbitas dos planetas são elípticas com uma excentricidade muito pequena.

Isso significa que a órbita não se afasta muito de um círculo, exceto em alguns casos, como o anão Plutão. Se aproximarmos as órbitas da forma circular, a aceleração do movimento do planeta é:

para_c = v²/r

Dado que F = ma, ter:

G mm /r² = m.v²/r

Aqui v É a velocidade linear do planeta ao redor do sol, suposição estática e em massa M, Enquanto o planeta é m. Então:

Pode servir a você: números significativos: regras, exemplos, exercícios resolvidos

Isso explica que os planetas mais distantes do sol têm uma velocidade orbital mais baixa, pois depende 1/√r.

Como a distância que o planeta está viajando é aproximadamente a duração da circunferência: L = 2πr e leva um tempo igual t, o período orbital, é obtido:

V = 2πr /t

Equalização de ambas as expressões para v uma expressão válida para t é obtida², O quadrado do período orbital:

E esta é precisamente a terceira lei de Kepler, pois nesta expressão o parêntese 4π² /Gm É constante, portanto T² é proporcional à distância r elevado ao cubo.

A equação definitiva para o período orbital é obtida extraindo a raiz quadrada:

Calculando a massa do sol

Quanto é a massa do sol? É possível descobrir através desta equação. Sabemos que o período orbital da Terra é de um ano e o raio orbital é 1 UA, equivalente a 150 milhões de quilômetros, por isso temos todos os dados necessários.

Em nossa equação anterior, limpamos M, Mas não antes de converter todos os valores para o sistema internacional de unidades se:

1 ano = 3.16 x 10⁷ segundos.

1 UA = 150 milhões de km = 1.5 x10^onze m.

E substituindo os dados da equação, obtemos uma estimativa bastante bem -sucedida do Sol do Sol em 2.0 x 10 ³⁰ kg.

Exercícios

Embora Kepler tivesse apenas os planetas em mente quando derivou suas famosas leis, elas também são válidas para o movimento de satélites e os outros órgãos do sistema solar, como veremos a seguir.

- Exercício 1

Saber que a órbita de Júpiter é 5.19 vezes maior que o da terra, encontre o período orbital de Júpiter.

Solução

De acordo com a definição de unidade astronômica, Júpiter é do Sol 5.19 UA, portanto, de acordo com a terceira lei de Kepler:

T²= r³= (5.19)³ anos

Portanto T = (5,19)^3/2  anos = 11.8 anos

- Exercício 2

Halley Comet visita o sol a cada 75.3 anos. Encontrar:

a) o principal semi -Hearing de sua órbita.

b) A medida do apelium, se o periélio me mencionar 0.568 UA.

Solução

Halley Comet visita o sol a cada 75.3 anos. Encontrar:

a) o principal semi -Hearing de sua órbita.

b) A medida do apelium, se o periélio me mencionar 0.568 UA.

Solução para

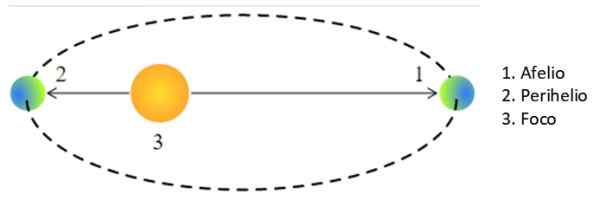
Quando um planeta ou qualquer outra estrela está em seu ponto mais próximo do sol, diz -se que está no Periélio, E quando estiver mais longe, em Aphelion. No caso especial de uma órbita circular, R na terceira lei de Kepler é o raio da órbita.

Pode atendê -lo: Constantes Antoine: fórmulas, equações, exemplos

No entanto, na órbita elíptica, o corpo celestial está mais ou menos longe do sol, sendo a semi -major "a" a média entre a aprototisa e o periélio:

Figura 3. Aflio e Periélio. Fonte: Wikimedia Commons. Pearson Scott Foresman / Domínio Público

Portanto, substituímos R por A na terceira lei de Kepler, que resulta em Halley em:

T²= a³→ a = (t)²³ → a = (75.3) ²³ UA = 17.832 UA

Solução b

A = ½ (periélio + apelio)

17.832 = ½ (0.568+ Aflio) → Aflio = 2 x 17.832 - 0.568 UA = 35.10 UA.

Experimentar

Analisar o movimento dos planetas requer semanas, meses e até anos de cuidadosa observação e registro. Mas em laboratório um experimento muito simples pode ser realizado para provar que a lei dos iguais de Kepler é cumprida.

Para isso, é necessário um sistema físico em que a força que governa o movimento é uma condição central e suficiente para que a lei das áreas seja cumprida. Esse sistema consiste em uma massa amarrada a uma corda longa, com a outra extremidade do fio fixo para um suporte.

A massa separa um pequeno ângulo de sua posição de equilíbrio e é impresso um leve impulso, de modo que executa um movimento oval (quase elíptico) no plano horizontal, como se fosse um planeta ao redor do sol.

Na curva descrita pelo pêndulo, podemos provar que ele varre áreas iguais em tempos iguais, sim:

-Consideramos os rádios vetoriais que variam do centro de atração (ponto de equilíbrio inicial) à posição da massa.

-E nós barmos entre dois momentos consecutivos de igual duração, em duas áreas diferentes do movimento.

Quanto mais tempo o fio do pêndulo e menor o ângulo que se afasta da vertical, a força restauradora líquida será mais horizontal e a simulação se assemelha ao caso do movimento com força central em um plano.

Então o oval descrito se aproxima de uma elipse, como a que os planetas viajam.

Materiais

-Tópico inextensível

-1 massa ou bola de metal pintada branca que atua como lentilha de pêndulo

-Governante

-Transportador

-Imagine a câmera com disco estroboscópio automático

-Apoia

-Duas fontes de iluminação

-Uma folha de papel ou papelão preto

Pode servir a você: Big Crunch Theory: História, princípios, dados a favor e contra

Procedimento

A montagem da figura é necessária para tirar fotos de vários flashes do pêndulo à medida que sua trajetória segue. Para fazer isso, você tem que colocar a câmera logo acima do pêndulo e do álbum Strobe Automatic na frente da lente.

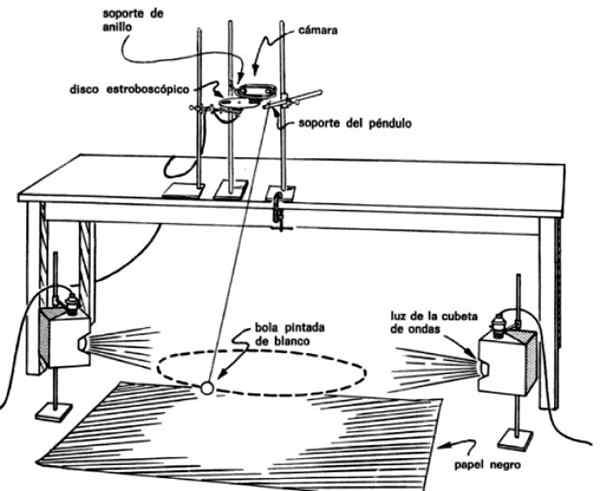Figura 4. Montagem do pêndulo para verificar se ele varre áreas iguais em tempos iguais. Fonte: Guia de laboratório PSSC.

Dessa forma, as imagens são obtidas em intervalos regulares do pêndulo, por exemplo, cada 0.1 ou cada 0.2 segundos, o que permite saber o tempo que levou para passar de um ponto para o outro.

Você também precisa iluminar a massa do pêndulo convenientemente, colocando as luzes em ambos os lados. A lentilha deve ser pintada de branco para melhorar o contraste no fundo, que consiste em um papel preto estendido no chão.

Agora você deve verificar se o pêndulo varre áreas iguais em tempos iguais. Para isso, um intervalo de tempo é escolhido e os pontos ocupados pelo pêndulo no referido intervalo são marcados no papel.

Na imagem, uma linha é extraída do centro do oval para esses pontos e, portanto, teremos a primeira das áreas varridas pelo pêndulo, que é aproximadamente um setor elíptico como o mostrado abaixo:

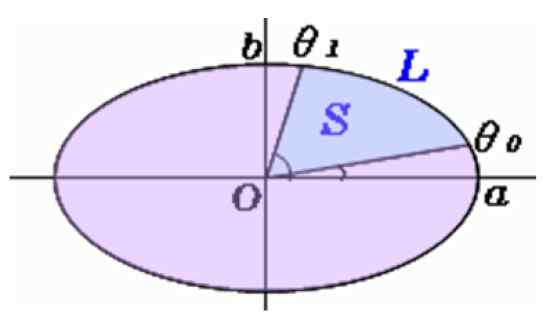Figura 5. Área de um setor elíptico. Fonte: f. Zapata.

Cálculo da área de seção elíptica

Os ângulos são medidos com o transportador θ_qualquer e θ₁, E esta fórmula é usada para encontrar s, a área do setor elíptico:

S = f (θ₁) - f (θ_qualquer)

Com F (θ) dado por:

Observe que para e b Eles são os semi -senijes maiores e menores, respectivamente. O leitor só deve se importar para medir cuidadosamente os semi -mess e os ângulos, pois existem calculadoras on -line para avaliar facilmente essa expressão.

No entanto, se você insistir em fazer o cálculo manualmente, deve se lembrar de que o ângulo θ é medido em graus, mas no momento da entrada nos dados da calculadora, os valores devem ser expressos em Radianos.

Então você deve marcar outro par de pontos em que o pêndulo investiu no mesmo intervalo de tempo e desenhe a área correspondente, calculando seu valor com o mesmo procedimento.

Verificação da lei de áreas iguais

Finalmente, resta verificar se a lei das áreas é cumprida, ou seja, que em tempos iguais as áreas iguais são varridas.

Os resultados se desviam um pouco do que esperou? Você deve ter em mente que todas as medidas são acompanhadas por seus respectivos erros experimentais.

Referências

1. Calculadora Online Keisan. Área de uma calculadora do setor elíptico. Recuperado de: Keisan.Casio.com.
2. OPENTAX. Lei de Movimento Planetário de Kepler. Recuperado de: OpenStax.org.
3. PSSC. Física de Laboratório. Editorial revertido. Recuperado de: livros.Google.co.
4. Palen, s. 2002. Astronomia. Série Schaum. McGraw Hill.
5. Pérez r. Sistema simples com força central. Recuperado de: Francesphysics.Blogspot.com
6. Stern, d. As três leis de Kepler do movimento planetário. Recuperado de: phy6.org.