Lei de Watt O que é, exemplos, aplicações

O Lei de Watt Aplica -se a circuitos elétricos e estabelece essa energia elétrica P Fornecido por um elemento de circuito, é diretamente proporcional ao produto entre a tensão de alimentação V do circuito e a intensidade da corrente Yo que circula através dele.

A energia elétrica é um conceito muito importante, porque aponta o quão rápido é um elemento transformar a eletricidade em alguma outra forma de energia. Matematicamente, a definição dada da lei de Watt é expressa da seguinte maneira:

P = v.Yo

figura 1. A energia elétrica indica a velocidade com que a eletricidade é transformada. Fonte: Pixabay

No sistema internacional de unidades (SI), a unidade de energia é chamada Watt E é abreviado W, em homenagem a James Watt (1736-1819), um engenheiro escocês pioneiro da Revolução Industrial. Como a energia é energia por unidade de tempo, 1 W é igual a 1 joule/segundo.

Todos estamos familiarizados com o conceito de energia elétrica de uma maneira ou de outra. Por exemplo, dispositivos elétricos domésticos de uso comum sempre trazem sua energia especificada, incluindo lâmpadas, beliches elétricos ou geladeiras, entre outros.

[TOC]

Lei de Watt e elementos de circuito

A lei de Watt se aplica a elementos de circuito com comportamento diferente. Pode ser uma bateria, uma resistência ou outra. Entre os fins do elemento, uma diferença de potencial é estabelecida V_B - V_PARA = V_Ab E a corrente circula na direção de A a B, conforme indicado na figura a seguir:

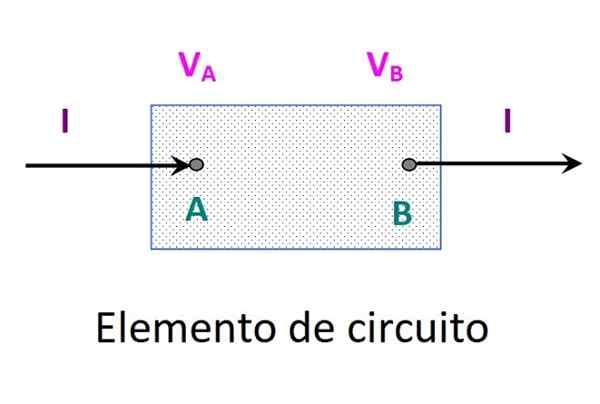Figura 2. Um elemento de circuito no qual uma diferença de potencial foi estabelecida. Fonte: f. Zapata.

Em um tempo muito pequeno Dt, Passar uma certa quantidade de carga DQ, para que o trabalho realizado seja dado por:

dw = v.DQ

Onde DQ Está relacionado ao atual como:

dq = i.Dt

Então:

Pode atendê -lo: anão vermelho

dw = v. Yo.Dt

dw/dt = V. Yo

E como o poder é trabalho por unidade de tempo:

P = v.Yo

-Sim v_Ab > 0, as cobranças que passam pelo elemento ganham energia potencial. O elemento fornece energia de uma fonte. Pode ser uma bateria.

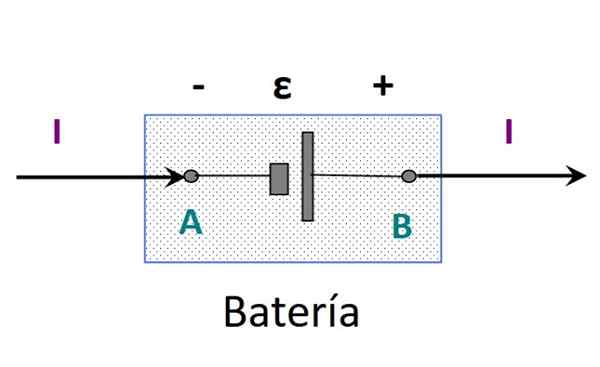Figura 3. Energia fornecida por uma bateria. Fonte: f. Zapata.

-Sim v_Ab < 0, las cargas pierden energía potencial. El elemento disipa energía, tal como una resistencia.

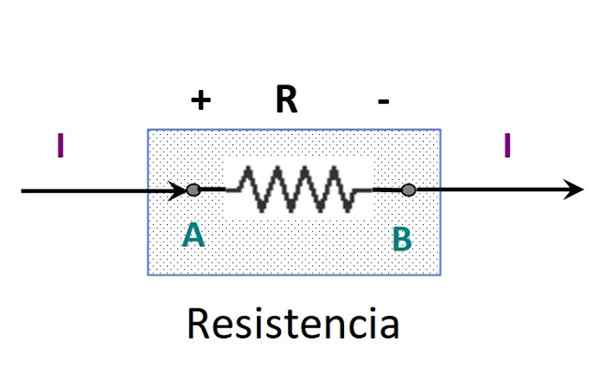Figura 4. Resistência transforma energia em forma de calor. Fonte: f. Zapata.

Observe que a potência fornecida por uma fonte não depende apenas da tensão, mas também da corrente. Isso é importante para explicar por que as baterias de carro são tão grandes, levando em consideração que elas mal fornecem 12 V.

O que acontece é que o motor inicial precisa de uma corrente alta, por um curto período de tempo, que fornece o poder necessário para iniciar o carro.

Lei de Watt e Lei de Ohm

Se o elemento do circuito for uma resistência, a lei de Watt e a lei de Ohm podem ser combinadas. O último estabelece que:

V = i. R

Isso substituindo a lei de Watt leva a:

P = v. Eu = (eu.R).I = i².R

Uma versão baseada em tensão e resistência também pode ser obtida:

P = v. (V/r) = V² / R

As possíveis combinações entre as quatro magnitudes: Power P, Corrente I, Tensão V e Resistência R. De acordo com os dados oferecidos por um problema, as fórmulas mais convenientes são escolhidas.

Por exemplo, suponha que em um certo problema seja solicitado para encontrar a resistência r, que está na sala inferior esquerda da letra.

Dependendo das magnitudes cujo valor é conhecido, algumas das três equações relacionadas (em verde) são escolhidas (em verde). Por exemplo, suponha que eles se conheçam V e Yo, então:

Pode servir a você: Pascal Princípio: História, Aplicações, Exemplos

R = v/ i

Se eles são conhecidos P e Yo, E resistência é solicitada, usada:

R = p / i²

Finalmente, quando eles se conhecem P e V, A resistência é obtida por:

R = p² /V

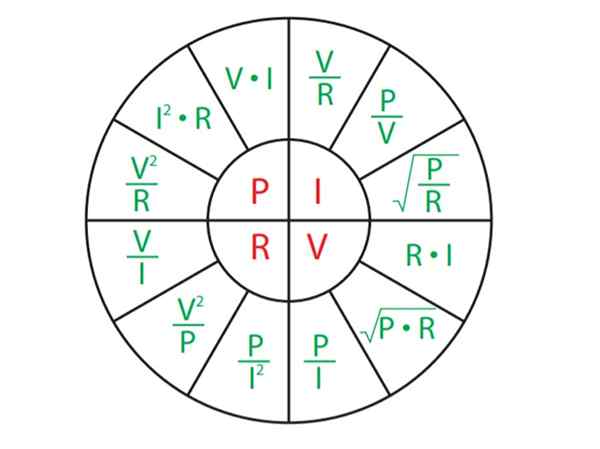Figura 5. Fórmulas da lei de Watt e a lei de Ohm. Fonte: f. Zapata.

Formulários

A lei de Watt pode ser aplicada em circuitos elétricos para encontrar a alimentação elétrica fornecida ou consumida pelo elemento. As lâmpadas são bons exemplos de aplicação da lei de Watt.

Exemplo 1

Uma lâmpada especial para obter várias iluminações em uma, tem dois filamentos de tungstênio, cujas resistências são r_PARA = 48 ohm e r_B = 144 ohm. Eles estão conectados a três pontos, indicados como 1, 2 e 3, como visto na figura.

O dispositivo é controlado por comutadores para selecionar os pares de terminais e também conectá -lo à rede de 120 V. Encontre todos os poderes possíveis que podem ser obtidos.

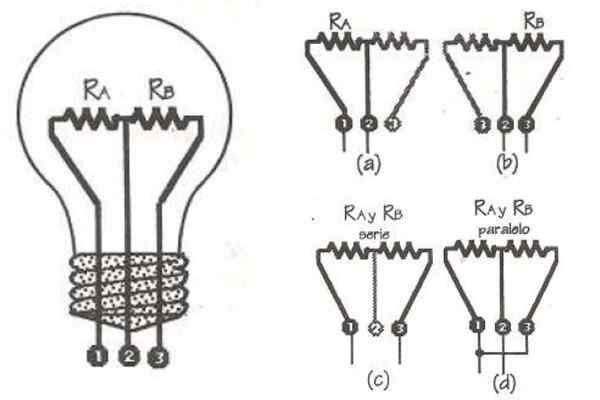Figura 6. Esquema para o exemplo resolvido 1. Fonte. D. Figueroa. Física para Ciência e Engenharia.

Solução

- Quando os terminais 1 e 2 se conectam, apenas resistência r_PARA É ativado. Como a tensão é obtida, que é 120 V e o valor da resistência, esses valores são diretamente substituídos na equação:

P = v²/R = (120 V)²/48 ohm = 300 w

- Terminais de conexão 2 e 3, resistência r é ativada_B, cujo poder é:

P = v²/R = (120 V)²/144 ohm = 100 w

- Os terminais 1 e 3 permitem que as resistências sejam conectadas em série. A resistência equivalente é:

R_Eq = R_PARA + R_B = 48 ohm + 144 ohm = 192 ohm

Portanto:

P = v²/R = (120 V)² /192 ohm = 75 W

- Finalmente, a possibilidade restante é conectar a resistência em paralelo, como mostrado no diagrama d). A resistência equivalente neste caso é:

1/ r_Eq = (1/r_PARA) + (1/r_B) = (1/48 ohm) + (1/144 ohm) = 1/36 ohm.

Portanto, a resistência equivalente é R_Eq = 36 ohm. Com este valor, o poder é:

Pode atendê -lo: propriedades elétricas dos materiais

P = v² / R = (120 V)² / 36 ohm = 400 W

Exemplo 2

Além do watt, outra unidade amplamente usada para energia é o Kilowatt (ou Kilowatt), abreviado como KW. 1 kW é igual a 1000 watts.

Empresas que fornecem eletricidade para residências na fatura em termos de energia consumida, não do poder. A unidade que eles usam é o Kilowatt-Hora (KW-H) que, apesar de tomar o nome de Watt, é energia para energia.

1 kilowatt-hora ou kw-h É a energia fornecida em 1 hora através de uma potência de 1000 watts, que em Joules seria equivalente a:

1 kw-h = 1000 w x 3600 s = 3.6 x 10 ⁶ J

a) Suponha que uma casa consome 750 kWh por um determinado mês. Qual será o valor da conta de eletricidade daquele mês? O seguinte plano de consumidor segue:

- Taxa básica: $ 14.00.

- Preço: 16 centavos/kWh até você atingir 100 kWh por mês.

- Os 200 kWh seguintes por mês têm um valor de 10 centavos/kWh.

- E acima de 300 kWh por mês, 6 centavos são cobrados/kWh.

b) Encontre o custo médio de eletricidade.

Solução para

- O cliente consome 750 kW-h por mês, portanto, excede os custos indicados em cada estágio. Nos primeiros 100 kWh, o valor monetário é: 100 kwh x 16 centavos /kwh = 1600 centavos = 16.00 $

- Os 200 kWh seguintes têm um custo de: 200 kWh x 10 centavos /kwh = 2000 centavos = 20.00 $.

- Acima desses 300 kW-h, o cliente consome 450 kW-h mais, para um total de 750 kW-h. O custo neste caso é: 450 kWh x 6 centavos /kwh = 2700 centavos = 27.00 $.

- Finalmente, todos os valores obtidos mais a taxa básica são adicionados, para obter o preço do recebimento daquele mês:

Preço a pagar = 14.00 $+ 16.00 $ +20.00 $+ 27.00 $ = $ 77.

Solução b

O custo médio é: 77 $ / 750 kWh = 0.103 $ /kw-h = 10.3 centavos /kWh.

Referências

1. Alexander, c. 2006. Fundações de circuito elétrico. 3º. Edição. McGraw Hill.
2. Berdahl, e. Introdução à eletrônica. Recuperado de: CCRMA.Stanford.ed.
3. Boylestad, r. 2011. Introdução à análise do circuito. 13. Edição. Pearson.
4. Associação de Reconstruções Elétricas. A calculadora da lei de OHM e Watt com exemplo. Recuperado de: ElectricalRebuilders.org
5. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 5. Eletricidade. Editado por Douglas Figueroa (USB).