Lei de fórmula Lenz, equações, aplicações, exemplos

O Lei de Lenz Ele estabelece que a polaridade da força eletromotora induzida em um circuito fechado, devido à variação no fluxo do campo magnético, é tal que se opõe à variação do referido fluxo.

O sinal negativo que é colocado na lei de Faraday leva em consideração a lei de Lenz, sendo a razão pela qual é chamada de Lei de Faraday-Lenz e que é expressa da seguinte maneira:

figura 1. Uma bobina toroidal é capaz de induzir correntes em outros motoristas. Fonte: Pixabay.

[TOC]

Fórmulas e equações

ε representa a força eletromotora induzida, abreviada como Fem, Φ É o fluxo do campo magnético e t é o tempo. Unidades no sistema internacional (SI) para Fem Eles são os volts (v).

Por sua parte, o fluxo do campo magnético Φ É definido pelo seguinte produto escalar:

Muito B como n São magnitudes de vetor e podem ser denotadas com negrito ou com uma flecha na letra. B É o vetor de campo magnético e n É o vetor unitário (magnitude igual a 1) perpendicular à superfície cruzada por B.

Na equação mostrada B É constante e a unidade para Φ No SI para o fluxo de campo magnético está o Weber (W):

1 weber = 1 tesla. metro²

Outra maneira de expressar Φ É o obtido usando a definição de produto escalar:

Φ = b.PARA.cos θ

Nesta equação, B É a magnitude do campo magnético (sem negrito ou seta, para distinguir o vetor de sua magnitude), a é a área da superfície cruzada pelo campo e θ é o ângulo entre os vetores B e n.

O fluxo do campo magnético pode variar de maneiras diferentes ao longo do tempo, para criar um Fem induzido em um loop - um circuito fechado - de área para. Por exemplo:

-Fazendo a variável de campo magnético ao longo do tempo: B = B (T), Mantendo a área e o ângulo constante, então:

-A área da SPASE pode variar, deixando as outras magnitudes constantes:

 -O ângulo entre B E a superfície varia com a rotação da SPASE, dessa maneira é obtida um gerador sinusoidal:

Melhor ainda se, em vez de um único loop, Nougas são usadas, nesse caso Fem Multiplique n vezes:

 É claro que o fluxo do campo magnético pode variar com qualquer combinação dessas formas, embora seja um pouco mais complicado descrever.

Formulários

A aplicação imediata da lei de Lenz é determinar o significado do Fem ou corrente induzida sem a necessidade de realizar qualquer cálculo. Considere o seguinte: Você tem um loop no meio de um campo magnético, como o que produz um ímã de barra.

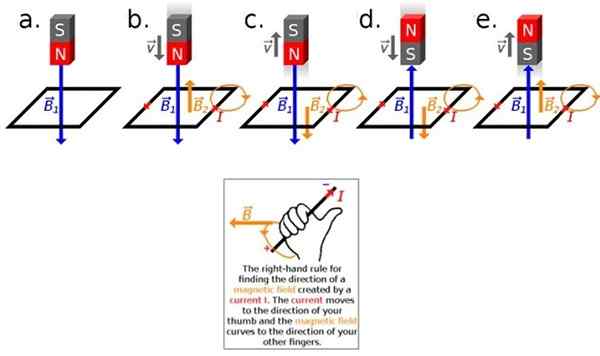Figura 2. Aplicação da lei de Lenz. Fonte: Wikimedia Commons.

Se o ímã e o loop estiverem em repouso, um em relação ao outro, nada acontece, ou seja, não haverá corrente induzida, porque o fluxo do campo magnético permanece constante nesse caso (veja a Figura 2a). Para induzir a corrente, é necessário que o fluxo varie.

Agora, se houver um movimento relativo entre o ímã e a SPASE, deslocando o ímã em direção à SPASE, ou estiver em direção ao ímã, será induzido a corrente para medir (Figura 2B em diante).

Essa corrente induzida, por sua vez, gera um campo magnético, portanto teremos dois campos: o do ímã B₁ em azul e o associado à corrente criada pela indução B₂, em laranja.

O régua do polegar direito permite que você conheça a direção de B₂, Para fazer isso, o polegar da mão direita é colocado na direção e direção que a corrente tem. Os outros quatro dedos indicam a direção em que o campo magnético é curvado, de acordo com a Figura 2 (abaixo).

Pode atendê -lo: espelho convexo

Movimento do ímã através da SPASE

Digamos que o ímã seja jogado em direção ao loop com seu poste norte direcionado para ele (Figura 3). As linhas de campo do ímã deixam o Pólo Norte N e entram no pólo do sul. Portanto, haverá mudanças em φ, o fluxo criado por B₁ que atravessa o loop:Φ aumenta!  Portanto, no loop, um campo magnético é criado B₂ Com intenção oposta.

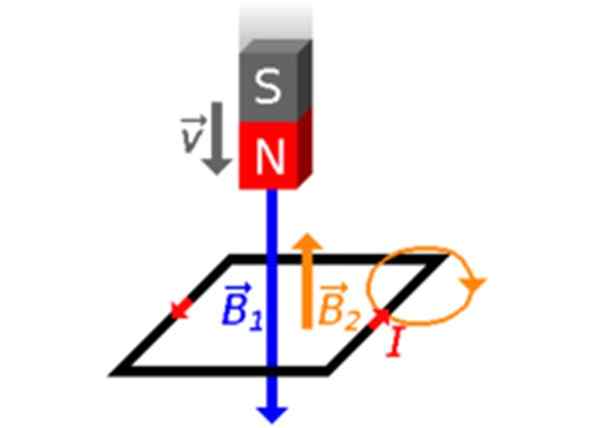Figura 3. O ímã se move em direção ao loop com seu poste norte para ela. Fonte: Wikimedia Commons.

A corrente induzida faz sentido contrária às agulhas do relógio, -Flechas Red nas Figuras 2 e 3-, de acordo com a regra do polegar direito.

Vamos afastar o ímã do Spira e depois o seu Φ diminui (Figuras 2C e 4), portanto, o loop é rápido em criar um campo magnético dentro B₂ Da mesma maneira, para compensar. Portanto, a corrente induzida é o tempo, como pode ser visto na Figura 4.

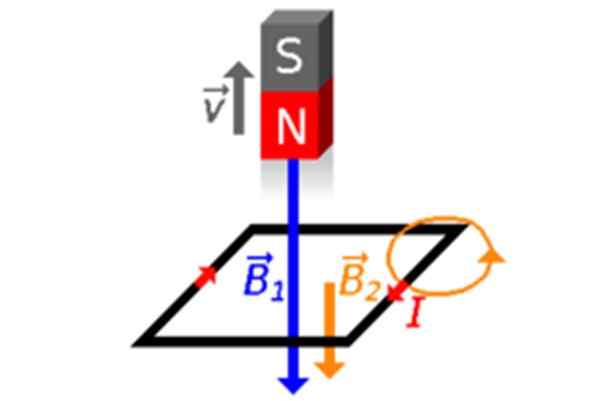Figura 4. O ímã se afasta do loop, sempre com seu poste norte apontando para ela. Fonte: Wikimedia Commons.

Investindo a posição do ímã

O que acontece se a posição do ímã for investida? Se o Polo Sul apontar para o loop, o campo aponta, já que as linhas de B Em um ímã, eles deixam o Pólo Norte e entram no Pólo Sul (veja a Figura 2D).

Imediatamente a lei de Lenz informa que esse campo vertical, precipitando em direção ao loop, induzirá um campo oposto nisso, ou seja,, B₂ para baixo e a corrente induzida também será tempo.

Finalmente ele se afasta do ímã de La Espira, sempre com seu poste sul apontando para o interior disso. Então, dentro do loop, há um campo B₂ Para contribuir para a remoção do ímã, não alterando o fluxo de campo. Muito B₁ como B₂ Eles terão o mesmo significado (veja a Figura 2d).

O leitor perceberá que, como prometemos, nenhum cálculo foi feito para conhecer a direção da corrente induzida.

Experimentos

Heinrich Lenz (1804-1865) realizou inúmeras obras experimentais ao longo de sua carreira científica. Os mais conhecidos são o que acabamos de descrever, dedicando -se a medir as forças e os efeitos magnéticos criados ao soltar abruptamente um ímã no meio de um loop. Com seus resultados, ele refinou o trabalho realizado por Michael Faraday.

Esse sinal negativo na lei de Faraday acaba sendo o experimento pelo qual é mais reconhecido hoje. No entanto, Lenz fez muitos empregos na geofísica durante sua juventude e, enquanto isso, ele se dedicou a soltar ímãs dentro das curvas e tubos. Ele também estudou resistência elétrica e condutividade metálica.

Em particular, nos efeitos do aumento da temperatura no valor da resistência. Ele continuou observando que, ao aquecer um fio, a resistência diminui e dissipa o calor, algo que James Joule também observou independentemente.

Para sempre lembrar suas contribuições para o eletromagnetismo, além da lei que leva seu nome, para as indutâncias (bobinas) elas são indicadas com a letra l.

Pode servir a você: teorema do tevenin: o que consiste, aplicativos e exemplos

Tubo de Lenz

É um experimento em que é demonstrado como um ímã para quando é liberado dentro de um tubo de cobre. O ímã ao cair, gera variações no fluxo do campo magnético dentro do tubo, como é o caso da espiral de energia.

Então é criada uma corrente induzida que se opõe à mudança no fluxo. O tubo cria seu próprio campo magnético para isso, que como já sabemos, está associado à corrente induzida. Suponha que o ímã seja liberado com o pólo sul (2d e 5).

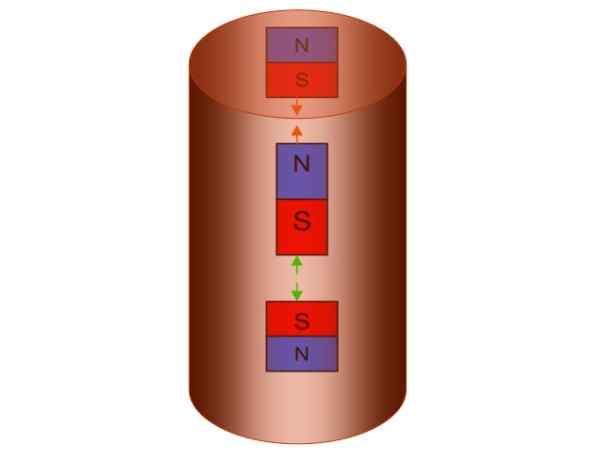Figura 5. Tubo de Lenz. Fonte: f. Zapata.

Como resultado, o tubo cria seu próprio campo magnético com um pólo norte para baixo e um pólo sul até em cima, o que equivale a criar alguns ímãs fictícios, um acima e outro abaixo daquele que está caindo.

O conceito está incorporado na figura a seguir, mas é necessário lembrar que os pólos magnéticos são inseparáveis. Se o ímã fictício inferior tiver um pólo norte, ele necessariamente acompanhará um sul para cima.

À medida que os pólos opostos atraem e os opostos repelem, o ímã que cai será repelido e, ao mesmo tempo, atraído pelo ímã fictício superior.

O efeito líquido sempre estará frenagem, mesmo que o ímã seja liberado com o Pólo Norte para baixo.

Lei de Joule-Lenz

A lei Joule-Lenz descreve como parte da energia associada à corrente elétrica que circula por um motorista é perdida na forma de calor, um efeito usado em aquecedores elétricos, pratos, secadores de cabelo e fogão elétrico, entre outros aparelhos.

Todos eles têm um elemento de resistência, filamento ou aquecimento que aquece até a passagem da corrente.

Em forma matemática, seja isso R A resistência do elemento de aquecimento, Yo a intensidade atual que circula através dele e t Tempo, a quantidade de calor produzido pelo efeito Joule é:

Q = i². R. t

Onde Q É medido em joules (unidades SI). James Joule e Heinrich Lenz descobriram esse efeito simultaneamente por volta de 1842.

Exemplos

Abaixo, mostramos três exemplos importantes nos quais a lei de Faraday-Lenz é aplicada:

Gerador atual alternado

Um gerador de corrente alternado transforma energia mecânica em energia elétrica. A fundação foi descrita no início: um loop é girado no meio de um campo magnético uniforme, como o que é criado entre os dois pólos de um grande eletromagnet. Quando usado N Espirais, o Fem aumenta proporcionalmente para N.

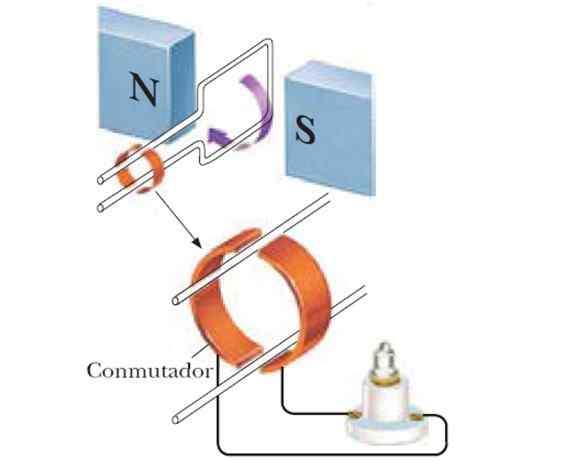Figura 6. O gerador de corrente alternado.

À medida que o loop é girado, o vetor normal para sua superfície muda sua orientação em relação ao campo, produzindo um Fem que varia de maneira sinusoidal ao longo do tempo. Suponha que a frequência angular de rotação seja Ω, Então, ao substituir a equação que ocorreu no início, será:

O transformador

É um dispositivo que permite obter uma tensão direta de uma tensão alternativa. O transformador faz parte de inúmeros dispositivos, como um carregador de telefone celular, por exemplo.Funciona da seguinte maneira:

Existem duas bobinas roladas em torno de um núcleo de ferro, uma é chamada Primário e a outra secundário.  O respectivo número de voltas é n₁ e n₂.

A bobina ou enrolamento primário é conectado a uma tensão alternativa (como eletricidade caseira, por exemplo) da forma V_P = V₁.cos ωt, causando uma corrente de frequência alternada para circular Ω.

Esta corrente origina um campo magnético que, por sua vez, causa um fluxo magnético oscilante na segunda bobina ou enrolamento, com uma tensão secundária da forma V_S = V₂.cos ωt.

No entanto, acontece que o campo magnético dentro do núcleo de ferro é proporcional ao inverso do número de voltas do enrolamento primário:

Pode servir a você: 13 exemplos da segunda lei de Newton na vida cotidiana

B ∝ 1 /N₁

E assim será V_P, a tensão no enrolamento primário, enquanto o Fem induzido V_S No segundo enrolamento, é proporcional, como sabemos, para o número de voltas n₂ e também para V_P.

Então, combinando essas proporcionalidades, há uma relação entre V_S e V_P que depende do quociente entre o número de voltas de cada uma, como segue:

V_S = (N₂ /N₁) V_P

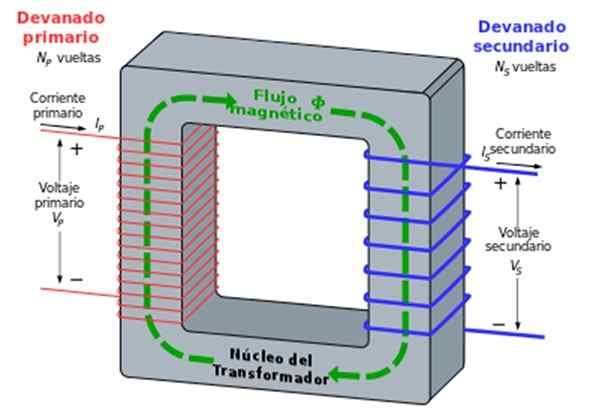Figura 7. O transformador. Fonte: Wikimedia Commons. Kundalinizero [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/]]

O detector de metal

São dispositivos usados ​​em bancos e aeroportos de segurança. Eles detectam a presença de qualquer metal, não apenas ferro ou níquel. Eles trabalham graças às correntes induzidas, através do uso de duas bobinas: um transmissor e outro receptor.

Uma corrente alternada de alta frequência é passada na bobina transmissora, de modo que gera um campo magnético alternativo ao longo do eixo (veja a figura), que induz uma corrente na bobina de recepção, algo mais ou menos semelhante ao que acontece com o transformador.

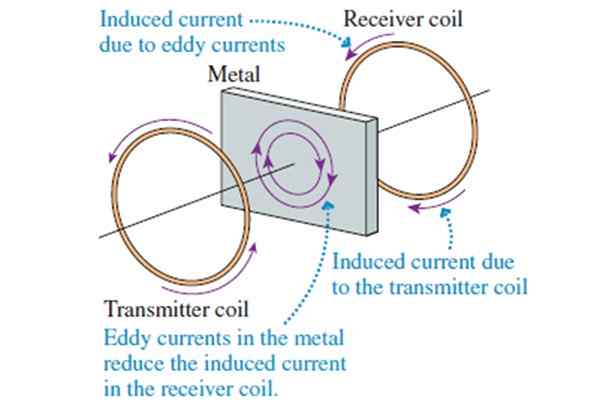Figura 8. Princípio de operação de detector de metais.

Se um pedaço de metal for colocado entre as duas bobinas, pequenas correntes induzidas aparecem nele, chamadas correntes de foucault (que não podem fluir em um isolador). A bobina de recebimento responde aos campos magnéticos da bobina transmissora e aqueles criados pelas correntes de Foucault.

As correntes de foucault tentam minimizar o fluxo de campo magnético na peça de metal. Portanto, o campo que percebe a bobina de recebimento diminui ao interferir uma peça de metal entre as duas bobinas. Quando isso acontece um alarme que avisa a presença de um metal.

Exercícios

Exercício 1

Há uma bobina circular com 250 empresas de raio de 5 cm, localizado perpendicular a um campo magnético de 0.2 t. Determinar o Fem induzido se em um intervalo de tempo de 0.1 s, o campo magnético magnético dobra e indicando o significado da corrente, de acordo com a seguinte figura:

Figura 9. Spira circular no meio de um campo magnético uniforme perpendicular ao plano da SPASE. Fonte: f. Zapata.

Solução

Primeiro, calcularemos a magnitude do MEM induzido, então o significado da corrente associado será indicado de acordo com o desenho.

N = 250 voltas

A = π. R² = p . (5 x 10^-2 m)² = 0.0079 m².

cos θ = cos 0 = 1 (O vetor n É preciso paralelo a B)

Como o campo magnético dobra sua magnitude, você tem:

Substituindo esses valores na equação para a magnitude do Fem Induzido:

ε = 250. 0.0079 m² . 2 t/s = 3.95 v

Desde que o campo dobrou, o fluxo de campo magnético também fez, portanto, no loop, é criada uma corrente induzida que se opõe ao referido aumento.

O campo na figura aponta para a tela. O campo criado pela corrente induzida deve deixar a tela, aplicando a regra do polegar direito, segue -se que a corrente induzida é anti -marária.

Exercício 2

Um enrolamento quadrado é composto de 40 voltas de 5 cm, que gira 50 Hz frequentemente no meio de um campo uniforme de magnitude 0.1 t. Inicialmente a bobina é perpendicular ao campo. Qual será a expressão para o Fem induzido?

Solução

Das seções anteriores, essa expressão foi deduzida:

ε = n.B.PARA. Ω. sin ωt

A = (5 x 10^-2 m)² = 0.0025 m²

N = 40 espirais

Ω = 2π.F = 2π.50 Hz = 100p s^-1

B = 0.1 t

ε = 40 x 0.1 x 0.0025 x 100π  x sen 50.t =p . Sen 100π.televisão

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Ciência física conceitual. 5 ª. Ed. Pearson.
3. Cavaleiro, r.  2017. Física para cientistas e engenharia: uma abordagem de estratégia. Pearson.
4. OpenX College. Lei de Indução de Faraday: Lei de Lenz. Recuperado de: OpenTextBC.AC.
5. Física Librettexts. Lei de Lenz. Recuperado de: Phys.Librettexts.org.
6. Sears, f. (2009). University Physics Vol. 2.