Lei de Gauss

Explicamos o que é a lei de Gauss, suas aplicações e colocamos exercícios resolvidos

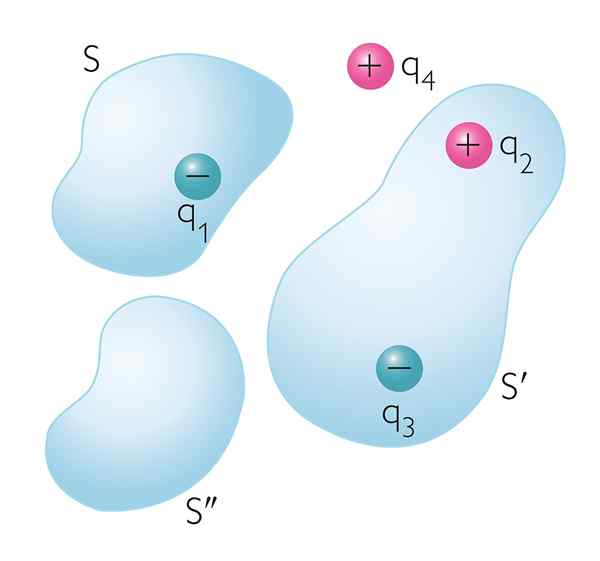
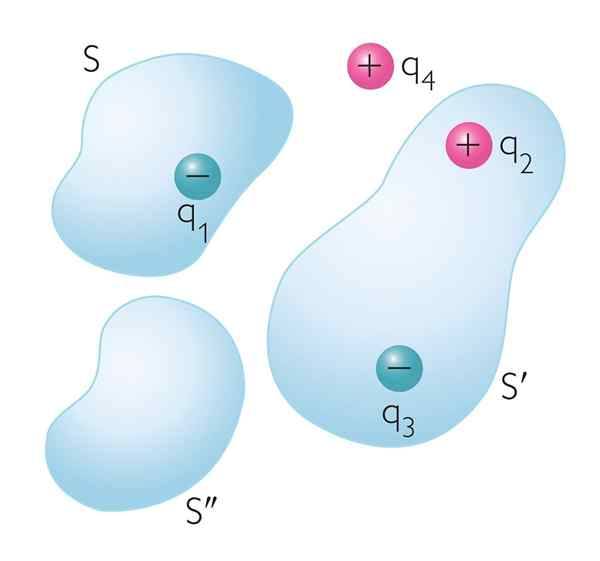figura 1. Cargas elétricas dentro e fora das superfícies gaussianas arbitrariamente. Somente cargas travadas dentro de cada superfície contribuem para o fluxo elétrico líquido através deles

Qual é a lei de Gauss?

O Lei de Gauss afirma que o fluxo do campo elétrico, através de uma superfície fechada imaginária, é proporcional ao valor de carga líquido das partículas encontradas dentro da referida superfície.

Denotando o fluxo elétrico através de uma superfície fechada, como Φ_E e para a carga líquida bloqueada pela superfície por Q_enf, Então a seguinte relação matemática é estabelecida:

Φ_E = C ∙ q_enf

Onde c É a constante da proporcionalidade.

Explicação da Lei de Gauss

Para entender o significado da lei de Gauss, é necessário explicar os conceitos envolvidos em sua declaração: carga elétrica, campo elétrico e campo de campo elétrico através de uma superfície.

Carga elétrica

A carga elétrica é uma das propriedades fundamentais da matéria. Um objeto carregado pode ter um dos dois tipos de carga: positivo ou negativo, embora normalmente os objetos sejam neutros, ou seja, eles têm a mesma quantidade de carga negativa que positiva.

Dois objetos carregados com o carregamento do mesmo tipo são repelidos mesmo quando não há contato um com o outro e estão no vácuo. Pelo contrário, quando cada um dos corpos tem um monte de sinal diferente, eles atraem. Este tipo de interação a distância é conhecido como interação elétrica.

No sistema internacional de unidades se a carga elétrica for medida em Culombios (C). O portador de carga elementar negativo é o elétron Com carga de -1,6 x 10^-19C E o portador de carga elementar positivo é o próton com um valor de carga +1,6 x 10^-19C. Normalmente os corpos carregados têm entre 10^-9C e 10^-3C.

Campo elétrico

Um corpo carregado eletricamente altera o espaço em seus arredores, enchendo -o com algo invisível chamado campo elétrico. Para saber que este campo está presente, é necessária uma carga de teste específica.

Pode atendê -lo: movimento harmônico simples

Se a carga de teste for colocada em um local onde houver um campo elétrico, uma força aparecerá em uma certa direção, que é a mesma do campo elétrico. A intensidade do campo é a força na carga de teste dividida pela quantidade de carga do mesmo. Então, as unidades de campo elétrico E No sistema internacional de unidades estão Newton entre Coulomb: [E] = n/c.

Cargas específicas positivas produzem um campo radial do lado de fora, enquanto cargas negativas produzem um campo radialmente direcionado para dentro. Além disso, o campo produzido por uma carga pontual decai com o inverso do quadrado da distância à referida carga.

Linhas de campo elétrico

Michael Faraday (1791 - 1867) foi o primeiro a ter uma imagem mental do campo elétrico, imaginando -o como linhas que seguem a direção do campo. No caso de uma carga pontual positiva, essas linhas são radiais a partir do centro. Onde as linhas estão mais juntas, o campo é mais intenso e menos intenso, onde são mais separados.

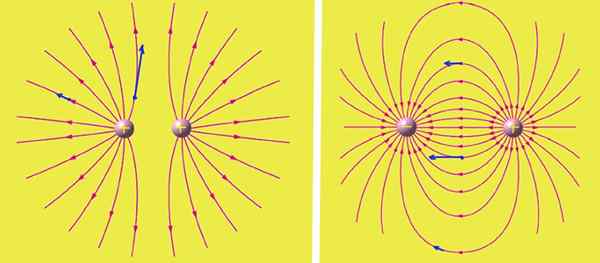Figura 2. Nas linhas de campo esquerdo de duas cargas iguais e positivas. À direita, as linhas de campo de carga de igual magnitude, mas sinais contrários. As setas azuis representam o vetor de campo elétrico em diferentes posições. Fonte: Wikimedia Commons.

As cargas positivas são as fontes de onde surgem as linhas de campo elétrico, enquanto as cargas negativas são as pias das linhas.

As linhas de campo elétricas não se fecham em si mesmas. Em um conjunto de cargas, as linhas deixam as cargas positivas e entram nas positivas, mas também podem chegar ou vir do infinito.

Pode servir a você: Equilíbrio estável: conceito e exemplos

Eles também não estão se cruzando e, em cada ponto do espaço, o vetor de campo elétrico é tangente à linha de campo e proporcional à densidade da linha lá.

Figura 3. A garota está eletricamente carregada por estar em contato com a cúpula de um gerador de van der Graaf. Seu cabelo segue as linhas de campo elétrico. Fonte: Wikimedia Commons.

Fluxo de campo elétrico

As linhas de campo elétrico se assemelham às linhas atuais de um rio que flui suavemente, a partir daqui o conceito de fluxo de campo elétrico nasce.

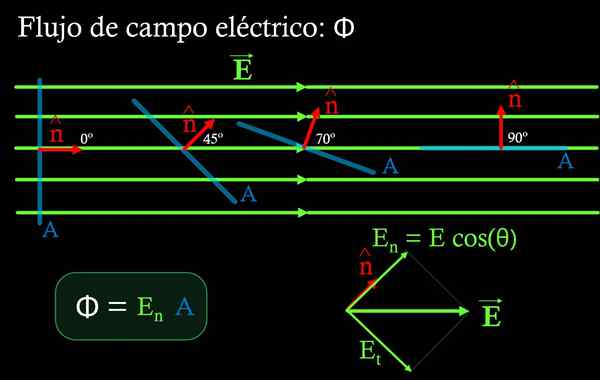Figura 4. O campo elétrico flui através de uma superfície de área a depende do ângulo formado entre a referida superfície e o campo e. O fluxo máximo é obtido quando a superfície é perpendicular ao campo e o fluxo é zero quando a superfície é paralela ao campo. Fonte: f. Zapata.

Em uma região onde o campo elétrico é uniforme, o fluxo φ através de uma superfície plana é o produto do componente normal do e_n à referida superfície, multiplicada pela área PARA da mesma:

Φ = e_n ∙ a

Componente e_n É obtido multiplicando a magnitude do campo elétrico pelo cosseno do ângulo formado entre o campo e o vetor de unidade normal para a superfície da área PARA. (Veja a Figura 4).

Gauss Law Applications

A lei de Gauss pode ser aplicada para determinar o campo elétrico produzido por distribuições de carga com um alto grau de simetria.

Campo elétrico de uma carga pontual

Uma carga pontual produz um campo elétrico radial que é extrovertido se a carga for positiva e recebida de outra forma.

Escolhendo como superfície gaussiana Uma esfera imaginária do rádio e concêntrica à carga q, em todos os pontos da superfície da referida esfera, o campo elétrico é de igual magnitude e sua direção é sempre normal à superfície. Então, neste caso, o fluxo do campo elétrico é o produto da magnitude do campo pela área total da superfície esférica:

Pode atendê -lo: mecânica de fluidos: história, que estudos, fundamentos

Φ = e ∙ a = e ∙ 4πr²

Por outro lado, a lei de Gauss estabelece que: φ = c ∙ q, sendo a constante da proporcionalidade c. Ao trabalhar em unidades do sistema de medidas internacionais, a constante c É o inverso do subsídio do vácuo, e a lei de Gauss é formulada da seguinte maneira:

Φ = (1/ε_qualquer) ∙ q

Incorporando o resultado obtido para o fluxo para a lei de Gauss é:

E ∙ 4πr² = (1/ε_qualquer) ∙ q

E pela magnitude de E resultado:

E = (1/4πε_qualquer) ∙ (Q/ R²)

Coincide totalmente com a lei de Coulomb do campo elétrico de uma carga pontual.

Exercícios

Exercício 1

Duas cargas específicas são encontradas dentro de uma superfície gaussiana arbitrária. Sabe-se que um deles tem um valor de +3 NC (3 nano-Coulomb). Se o fluxo do campo elétrico líquido através da superfície gaussiana for 113 (n/c) m², Qual será o valor da outra carga?

Solução

A lei de Gauss estabelece isso

Φ_E = (1/ε_qualquer) ∙ q_enf

A partir daí, a carga líquida bloqueada é:

Q_enf = Φ_E ∙ ε_qualquer

Substituindo os resultados dos dados:

Q_enf = 113 (n/c) m² ∙ 8,85 x 10^-12 (C² m^-2 N^-1) = 1 x 10^-9 C = 1 nc.

Mas Q_enf = +Q - Q, Onde a carga positiva tem um valor conhecido de +3 NC, portanto, a carga será necessariamente -2 nc.

Exercício 2

Na Figura 2, há um arranjo (à esquerda) de duas cargas positivas, cada uma com valor +q e outro arranjo (à direita) com uma carga +q e o outro -q. Cada arranjo está bloqueado em uma caixa imaginária com todas as suas bordas de 10 cm. Sim | Q | = 3 μC, encontre o fluxo líquido de campo elétrico através da caixa para cada arranjo.

Solução

No primeiro arranjo, o fluxo líquido é:

Φ_E = (1/ε_qualquer) ∙ ( + q + q) = 678000 (n/c) m²

No arranjo certo, o fluxo líquido através da caixa imaginária que contém o torque de cargas é zero.

Referências

1. Cosenza, m. Eletromagnetismo. Universidade dos Andes.
2. Díaz, r. Eletrodinâmica: Notas de classe. universidade nacional da Colômbia.
3. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB).
4. Jackson, J. D. Electodinâmica clássica. 3º. Ed. Wiley.
5. Tarazona, c. Introdução à eletrodinâmica. Universidade Editorial Manuela Beltrán.