Ampère Fórmula e Lei das Equações, demonstração, exercícios

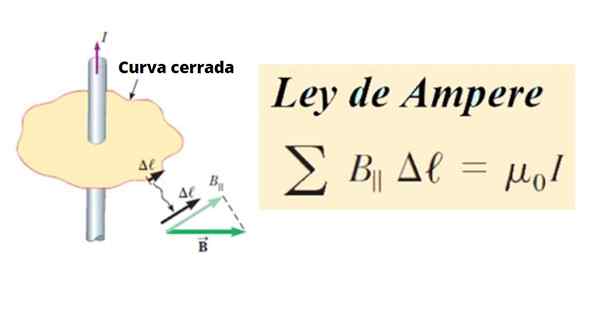
O Lei de Ampère afirma que a circulação do vetor de indução magnética B É proporcional à intensidade e da corrente que flui pela mesma.

Por sua vez a circulação de B É a soma de todos os produtos entre o componente tangencial B_║ e o comprimento de um pequeno segmento Δℓ de uma curva fechada C, Em torno de um circuito. Em termos matemáticos, está escrito assim:

∑ b_║ .Δℓ ∝ Yo

figura 1. Definição da lei de amperes. Fonte: Serway, r. Física da faculdade.

Como uma linha ou curva arbitrária, ela pode ser dividida em pequenos segmentos Δℓ, E estes por sua vez podem ser infinitesimais, então são chamadosℓ.

Nesse caso, a soma se torna uma linha integrante do produto escalar entre os vetores B e ds. Este produto contém o componente tangencial de B, que é b cosθ, onde θ é o ângulo entre os vetores:

O pequeno círculo que atravessa a integral significa que a integração é realizada em uma trajetória fechada C, que neste caso envolve a corrente que flui através da seção transversal do motorista.

A constante de proporcionalidade necessária para estabelecer a igualdade é μ_qualquer, Permeabilidade a vácuo. Dessa maneira, permanece a lei de Ampère:

A lei de Ampère nos diz que a linha integral ∫_C B ∙ ds Vale exatamente μ_qualquerEu, mas não nos oferece os detalhes sobre como o campo magnético é orientado B Em relação à curva c em cada ponto, ou sobre como calcular a integral. Isso nos diz que o resultado do mesmo é sempre μ_qualquerYo.

[TOC]

Demonstração da lei de Ampère

A lei de Ampère é verificada verificando experimentalmente o campo magnético produzido por um condutor retilíneo muito longo. Antes de resolver o problema, dois casos de interesse especial na equação anterior devem ser destacados:

Pode servir a você: corpos luminosos: características e como elas geram sua própria luz

-O primeiro é quando B e ds Eles são paralelos, o que significa que B é tangencial a C. Então o ângulo entre os dois vetores é 0º e o produto escalar é simplesmente o produto das magnitudes B.ds.

-O segundo ocorre se B e ds Eles são perpendiculares; nesse caso, o produto escalar é 0, uma vez que o ângulo entre os vetores é 90º, cujo cosseno é 0.

Outro detalhe importante é a escolha da curva c na qual a circulação de campo é avaliada. A lei de Ampère não especifica o que pode ser, mas deve embrulhar a distribuição atual. Nem diz como viajar a curva e há duas possibilidades para isso.

A solução é atribuir sinais de acordo com a regra do polegar direito. Os quatro dedos são curvos na direção em que você deseja integrar, geralmente isso será o mesmo no campo B circula. Se os pontos atuais na direção do polegar direito, um sinal será atribuído e, se não, assine -.

Isso se aplica quando há uma distribuição com várias correntes, alguns podem ser positivos e outros negativos. A soma algébrica deles é o que vamos colocar na lei de Ampère, que geralmente é nomeada como Atual corrente (Para a curva c).

Campo magnético do fio retilíneo e infinito

A Figura 2 mostra um fio que transporta uma corrente e fora do avião. A regra do polegar direito garante que B Ele circula na direção oposta, descrevendo circunferências como as setas vermelhas mostram.

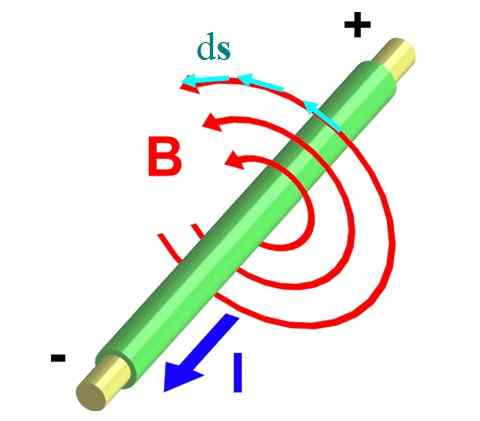Figura 2.- Campo magnético de um fio infinito. Fonte: Wikimedia Commons.

Vamos pegar um deles, cujo raio é r. Nós o dividimos em pequenos segmentos diferenciais Ds, representado por meio de vetores azuis. Ambos os vetores, B e ds, Eles são paralelos em cada ponto da circunferência e, dessa maneira, a integral ∫_C B ∙ ds Ele se transforma em:

Pode atendê -lo: corrente direta

∫_C Bds

Isso ocorre porque, como dissemos antes, o produto escalar B ∙ ds  É o produto das magnitudes dos vetores pelo cosseno 0º. O resultado da integral é conhecido graças à lei de Ampère, portanto escrevemos:

∫_C BDS = μ_qualquerYo

Como a magnitude do campo é constante em toda a trajetória, deixa a integral:

B ∫_C Ds = μ_qualquerYo

A integral ∫_C DS representa a soma de todos os segmentos infinitesimais que compõem a circunferência do rádio r, Equivalente ao seu comprimento, o produto de seu raio por 2π:

B.2πr = μ_qualquerYo

E a partir daí descobrimos que a magnitude de B é:

B = μ_qualquerI / 2πr

É necessário enfatizar que, mesmo que a trajetória selecionada (ou circuito ampérico) Não circular, o resultado da integral continua a ser μ_qualquerEu, no entanto ∫_C B ∙ ds Não seria mais B.2πr.

É por isso que a utilidade da lei de Ampère para determinar o campo magnético está na escolha de distribuições com alta simetria, de modo que a integral seja fácil de avaliar. Trajetórias circulares e retilíneas atendem a este requisito.

Exercícios resolvidos

- Exercício 1

Considere as curvas A, B, C e D mostradas na Figura 3. Eles envolvem três correntes, duas que deixam o avião, simbolizadas com um ponto ( . ), cujas intensidades são 1 a e 5 a, e uma corrente que entra no avião, que é denotada com uma cruz e cuja magnitude é 2 a.

Encontre a corrente incluída por cada curva.

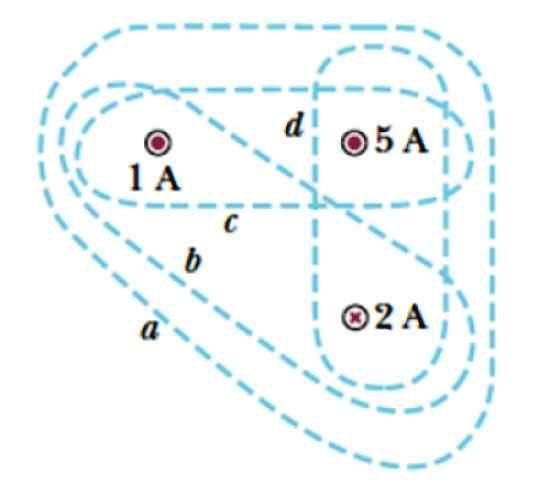Figura 3. Várias curvas para aplicar a lei de Ampère. Fonte: Serway, r. Física da faculdade.

Solução

As correntes que deixam o papel recebem um sinal +. De acordo com isso:

Pode atendê -lo: ondas superficiais: características, tipos e exemplos

Curva a

Envolve as três correntes, portanto a corrente fechada é + 1 a + 5 a - 2 a = 4 a.

Curva b

Somente as correntes de 1 a y - 2 a estão dentro dessa curva, portanto a corrente fechada é de - 2 a.

Curva c

Contém as correntes de saída 1 e 5 a, portanto a corrente fechada é 6 a.

Curva d

As correntes internas são +5 a e - 2 a, depois envolve uma corrente líquida de 3 a.

- Exercício 2

Calcule a magnitude do campo magnético produzido por um fio retilíneo muito longo.

Solução

De acordo com a lei de Ampère, o campo de arame é dado por:

B = μ_qualquerI / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 T.

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB).
2. Cavaleiro, r.  2017. Física para cientistas e engenharia: uma abordagem de estratégia.  Pearson.
3. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 2.
4. Serway, r. 2009. Física da faculdade. Cengage Learning.
5. Tipler, p. (2006) Física para ciência e tecnologia. 5ª ed. Volume 2. Editorial revertido.