Características convergentes da lente, tipos e exercícios resolvidos

As Lentes convergentes Eles são aqueles que são mais espessos em sua parte central e mais fina nas bordas. Como conseqüência, eles se concentram (converge) em um único ponto os raios de luz que os afetam em paralelo ao eixo principal. Este ponto é chamado de foco, ou foco de imagem, e é representado com a letra f. Lentes convergentes ou positivas formam o que é chamado de imagens reais de objetos.

Um exemplo típico de lente convergente é uma lupa. No entanto, é comum encontrar esse tipo de lente em dispositivos muito mais complexos, como microscópios ou telescópios. De fato, um microscópio composto básico é o constituído por duas lentes convergentes que têm uma pequena distância focal. Essas lentes são chamadas de alvo e ocular.

Lupa, uma lente convergente. 

As lentes convergentes são usadas na óptica para diferentes aplicações, embora talvez a mais conhecida seja corrigir os defeitos de visualização. Assim, eles são indicados para lidar.

[TOC]

Caracteristicas

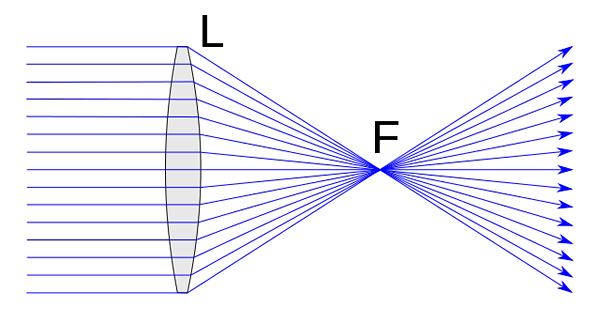Lente convergente. ChetVorno [CC0]

As lentes convergentes têm uma série de recursos que os definem. De qualquer forma, talvez o mais importante seja o que já avançamos em sua definição. Assim, as lentes convergentes são caracterizadas por desviar o foco qualquer raio que as afete em uma direção paralela ao eixo principal.

Além disso, de maneira recíproca, qualquer raio de incidente que passe o foco é refratado paralelo ao eixo óptico da lente.

Elementos de lentes convergentes

Diante do seu estudo, é importante saber quais elementos constituem as lentes em geral e lentes convergentes em particular.

Em geral, é chamado de centro óptico de uma lente até o ponto pelo qual todo raio que passa por ele não experimenta nenhum desvio.

O eixo principal é a linha que se junta ao centro óptico e ao foco principal, que já comentamos que é representado com a letra f.

Pode servir a você: TON: Transformações, equivalências e exercícios resolvidos

É chamado de foco principal até o ponto em que todos os raios que afetam a lente em paralelo ao eixo principal são encontrados.

A distância entre o centro óptico e o foco é chamada de distância focal.

Os centros de curvatura são definidos como os centros das esferas que criam a lente; sendo, por outro lado, os rádios da curvatura os rádios das esferas que dão origem à lente.

E finalmente, é chamado de plano óptico para o plano central da lente.

Formação de imagens em lentes convergentes

Diante da formação de imagens em lentes convergentes, uma série de regras básicas que são explicadas abaixo deve ser levada em consideração.

Se o raio afetar a lente em paralelo ao eixo, o raio emergente converge na imagem de foco. Inversamente, se um raio de incidente atravessa o foco do objeto, o raio surge em uma direção paralela ao eixo. Finalmente, os raios que cruzam o centro óptico são refratados sem experimentar nenhum desvio.

Como conseqüência, em uma lente convergente, você pode dar as seguintes situações:

- Que o objeto está localizado em relação ao plano óptico a uma distância maior que o dobro da distância focal. Nesse caso, a imagem que ocorre é real, invertida e menor que o objeto.

- Que o objeto está localizado a uma distância do plano óptico igual a duas vezes a distância focal. Quando isso acontece, a imagem obtida é uma imagem real e invertida e do mesmo tamanho que o objeto.

- Que o objeto está à distância do plano óptico entre uma e duas vezes a distância focal. Portanto, uma imagem é produzida é real, invertida e maior que o objeto original.

- Que o objeto está localizado a uma distância do plano óptico menor que a distância focal. Nesse caso, a imagem será virtual, direta e maior que o objeto.

Pode servir a você: choque magnético: unidades, fórmulas, cálculo, exemplos

Tipos de lente convergente

Existem três tipos diferentes de lentes convergentes: lentes biconvexas, lentes Planoconvex e lentes Concavoconvexas.

As lentes biconvexas, como o nome indica, são compostas por duas superfícies convexas. Planoconvexas, enquanto isso, tem uma superfície plana e outro convexo. E, finalmente, as lentes concavoconvexas são constituídas por uma superfície ligeiramente côncava e outro convexo.

Diferença com lentes divergentes

Lente convergente. Fir0002 (Talk) (Uploads) [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/]]

Lentes divergentes, por outro lado, diferem do convergente, pois a espessura diminui das bordas em direção ao centro. Assim, ao contrário do que aconteceu com o convergente, nesse tipo de lentes os raios de luz que afetam o eixo principal em paralelo. Dessa forma, eles formam o que é chamado de imagens virtuais de objetos.

Na óptica, lentes divergentes ou negativas, como também são conhecidas, são usadas principalmente para corrigir a miopia.

Equações de Gauss de lentes finas e lentes aumentadas

Em geral, o tipo de lentes estudadas são aquelas chamadas lentes finas. Estes são definidos como aqueles que têm uma pequena espessura em comparação com a curvatura das superfícies que os limitam.

Este tipo de lente pode ser estudado com a equação de Gauss e com a equação que permite determinar o aumento de uma lente.

Equação de Gauss

A equação de Gauss de lentes finas serve para resolver a multidão de problemas básicos de óptica. Daí sua grande importância. Sua expressão é a seguinte:

1/f = 1/p +1/q

Onde 1/ f é o que é chamado de poder de uma lente e f é a distância ou distância focal do centro óptico para o focam. A unidade de medida do poder de uma lente é a dioptria (d), sendo 1 d = 1 m^-1. Por sua vez, p e q são respectivamente a distância em que um objeto e a distância à qual sua imagem é observada.

Pode servir a você: Teoria do Big Bang: características, estágios, evidências, problemas

Aumento da lente

O aumento lateral em uma lente fina é obtida com a seguinte expressão:

M = - Q / P

Onde m é o aumento. A partir do valor do aumento, uma série de consequências pode ser deduzida:

Sim | M | > 1, o tamanho da imagem é maior que o do objeto

Sim | M | < 1, el tamaño de la imagen es menor que el del objeto

Se m> 0, a imagem está certa e do mesmo lado da lente que o objeto (imagem virtual)

sim m < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)

Exercício resolvido

Um corpo está localizado a um metro de uma lente convergente, que tem uma distância focal de 0, 5 metros. Como será a imagem do corpo? Quão longe você vai encontrar?

Temos os seguintes dados: p = 1 m; F = 0,5 m.

Substituímos esses valores na equação de Gauss das lentes finas:

1/f = 1/p +1/q

E os seguintes permanecem:

1/0,5 = 1 + 1/q; 2 = 1 + 1/q

Limparemos 1/q

1/q = 1

Para então limpar Q e obter:

Q = 1

A partir daí, substituímos a equação do aumento de uma lente:

M = -q / p = -1 / 1 = -1

Portanto, a imagem é real desde Q> 0, invertida porque M < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.

Referências

1. Luz (n.d.). Na Wikipedia. Recuperado em 18 de março de 2019, deste.Wikipedia.org.
2. Lekner, John (1987). Teoria da reflexão, de ondas eletromagnéticas e parlamentares. Springer.
3. Luz (n.d.). Na Wikipedia. Recuperado em 20 de março de 2019, de.Wikipedia.org.
4. Lente (n.d.). Na Wikipedia. Recuperado em 17 de março de 2019, deste.Wikipedia.org.
5. Lente (óptica). Na Wikipedia. Recuperado em 19 de março de 2019, de.Wikipedia.org.
6. Atos, Eugene (2002). Óptica (4ª ed.). Addison Wesley.
7. Tupler, Paul Allen (1994). Físico. 3ª edição. Barcelona: Eu revertei.