Lados homólogos

Explicamos quais são os lados homólogos, com exemplos e exercícios resolvidos

O que são lados homólogos?

O lados homólogos Em duas figuras geométricas planas são aquelas que se correspondem, mantendo a semelhança. Por exemplo, a mão direita de uma pessoa é homóloga com a mão direita de outra pessoa.

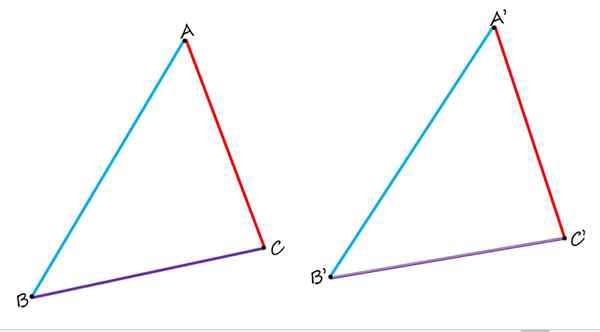
Na geometria plana, não existem apenas lados homólogos, mas vértices e ângulos homólogos também. Para ver, considere a figura a seguir, que consiste em dois triângulos idênticos ABC e A'B'C ':

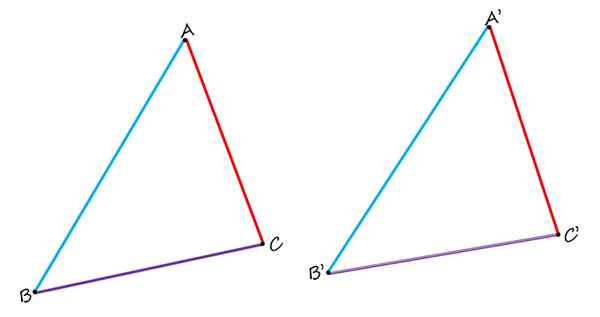Nos dois triângulos idênticos mostrados, o AB e A'B ', são homólogos, assim como os lados BC e B'C' e AC e A'C '. Fonte: f. Zapata.

Ao compará -los, observa -se claramente que os lados ab e a'b 'em azul são homólogos, pois ocupam uma posição semelhante em cada triângulo. Os lados BC e B'C 'em roxo também são homólogos. E, finalmente, o lado vermelho do AC é homólogo ao lado A'C '.

Explicação

Do acima mencionado, segue -se que os lados homólogos são aqueles que ocupam a mesma posição relativa em figuras da mesma maneira. Na imagem anterior, dois triângulos idênticos foram usados ​​para mostrar a idéia, mas isso pode generalizar facilmente outras figuras geométricas planas, formadas por lados consecutivos que fecham.

Esses números são chamados Polígonos. Por exemplo, triângulos e quadriláteros são polígonos de 3 e 4 lados, respectivamente.

O conceito de lados homólogos é importante porque permite definir critérios de similaridade entre polígonos, como será visto em breve. Os números semelhantes têm exatamente a mesma forma e mantêm a proporção idêntica entre os lados, mesmo que não tenham o mesmo tamanho.

E embora até agora tenha sido feita apenas a figuras planas, também existem figuras semelhantes em três dimensões. Eles são facilmente observados nas prateleiras de supermercados, quando o mesmo produto é vendido em recipientes idênticos, mas com um tamanho diferente.

Pode atendê -lo: lógica matemática

Outras palavras que são usadas de forma intercambiável na geometria para se referir a lados homólogos em figuras geométricas são: lados correspondentes, lados respectivos e lados equivalentes.

Vértices e ângulos homólogos

Como nos lados, também são definidos vértices homólogos, o que une pares de lados homólogos. Por exemplo, os vértices A e 'da figura anterior são homólogos. Da mesma forma, os pares de vértices B e B 'e C e C' são homólogos.

Finalmente, ângulos homólogos ocupam a mesma posição relativa nas figuras. Os vértices de ângulos homólogos são homólogos.

Para ilustrar a idéia, pegue o ângulo entre os lados azul e roxo do triângulo esquerdo, que pode ser denotado como eroBC. Este ângulo tem sua contraparte no ângulo quina'b'c ', do triângulo à direita.

O vértice deste ângulo é B, que, como indicado anteriormente, é uma contraparte com B ', e os outros dois pares de ângulos homólogos dos triângulos mostrados são:

• Portebca e porteb'c'a '
• Portecab e portec'a'b '

Similaridade de polígonos

Para que dois polígonos sejam semelhantes, as seguintes condições devem ser atendidas:

• Todos os pares de ângulos homólogos têm a mesma medida
• Seus pares de lados homólogos são proporcionais.

As duas condições devem ser atendidas simultaneamente para garantir a similaridade. É imediatamente observado por que.

Na figura seguinte, existem dois quadriláteros que obviamente não são semelhantes. É devido ao fato de que o primeiro status do semanal é cumprido, mas o segundo não:

Dois quadrilásteros que não são semelhantes, embora seus ângulos homólogos tenham igual medida. Fonte: f. Zapata.

Enquanto nos números seus pares de ângulos homólogos têm a mesma medida, porque todos são ângulos retos (eles medem 90º), os números não são semelhantes, porque seus pares de lados não são proporcionais.

Pode atendê -lo: função injetiva: o que é consiste, para que é e exemplos

Por outro lado, esses dois quadriláteros têm lados homólogos com igual medida, mas os ângulos homólogos não medem o mesmo. Portanto, os números claramente não são semelhantes.

Dois quadrilásteros com lados homólogos da mesma medida, mas com diferentes ângulos internos, portanto não são figuras semelhantes. Fonte: f. Zapata.

Razão de similaridade

Se dois números são semelhantes, o quociente entre os lados homólogos é o mesmo e é chamado razão de similaridade.

Denotando os lados de uma das figuras como A, B, C, D ... e as correspondentes da outra figura como A ', B', C ', D

Perímetros e áreas de números semelhantes

O índice de similaridade permite obter relações entre os perímetro, áreas e volumes de duas figuras semelhantes.

Perímetro Razão para dois números semelhantes

O perímetro P de um polígono é definido como a soma de todos os seus lados. Se você tem uma figura cujos lados são ', b', c ', d' ..., seu perímetro P 'é:

P '= a' + b ' + c' + d '.. .

Se outro polígono é semelhante a isso, e seus lados são A, B, C, D ..., é cumprido que:

E, por conseguinte:

A = r ∙ a '

Você pode afirmar o mesmo para os outros lados desta figura. Portanto, o perímetro P é expresso como:

P = A + B + C + D .. . = r ∙ a ' + r ∙ b' + r ∙ c ' + r ∙ d' +…

Como "R" é um fator comum para todos os viciados, a relação entre P e P 'é:

P = r ∙ p '

Isso significa que a razão para os perímetros entre dois polígonos semelhantes é igual ao motivo da similaridade.

Razão para áreas de dois números semelhantes

Se duas figuras semelhantes têm respectivamente as áreas A e A ', elas estão relacionadas através de:

Pode atendê -lo: exercícios de liberação de fórmula

A = r²∙ a '

Onde "r" é a razão da similaridade das figuras.

Razão de volume de dois números semelhantes

São duas figuras tridimensionais semelhantes, cujos volumes são, respectivamente, V e V '. A relação entre eles, através de "R" é:

V = r³∙ V '

Exemplos

Plantas

Partes de uma terra, a planta de um edifício ou até uma peça de roupa, em uma escala menor em uma folha de papel pode ser representada. Os planos têm a vantagem de poder levar com eles e fazer as modificações pertinentes facilmente, antes de serem praticadas no objeto real.

Mapas

Eles geralmente são representações no plano de uma grande área de terra, de uma vila aos continentes. Eles também são feitos em uma certa escala.

Eles têm inúmeras aplicações e existem muitos tipos. Por exemplo, através de um mapa, o terreno pode ser descrito e, quando está localizado em um ponto específico, o melhor caminho a seguir desse ponto para outro é determinado.

Modelos

São representações tridimensionais na escala de objetos como carros, edifícios e construções em geral.

Exercício resolvido

Os seguintes valores correspondem aos lados de alguns triângulos semelhantes. Encontre o motivo da similaridade e dos valores de "X" e "Y":

Triângulo 1: 5, 8, 10

Triângulo 2: 150, x, y

Solução

O motivo da similaridade é o quociente:

R = 150/5 = 30

Portanto:

x = 30 × 8 = 240

y = 10 × 30 = 300