Isocuantas e isocostos

Quais são os isocuantas e isocostos?

As Isocuantas e isocostos Existem dois tipos diferentes de curvas que são mostradas como representações gráficas para um empreendedor para determinar o método de produção mais eficiente para sua empresa, ou seja, aquele com o menor custo total por unidade produzida.

Uma isocounta é uma curva na qual as várias combinações de dois fatores de produção específicos, como uma quantidade de mão -de -obra e máquinas, geram a mesma quantidade produzida. Isto é, é uma curva ao longo da qual a taxa de produção máxima é constante.

Eles também são conhecidos como curvas de produção constantes. Portanto, uma curva de isocounta indica as várias combinações de dois fatores de produção que dão ao produtor o mesmo nível de produção por unidade de tempo.

Conhecendo a natureza dos isocados, através das linhas de Isochotos, os custos desses fatores são considerados.

Uma linha de isochow representa as diferentes combinações de dois fatores de produção específicos que uma empresa pode comprar pela mesma quantia em dinheiro, com o custo, pois cada fator tem.

Diferenças e exemplos

Um empresário poderia usar todo o seu capital apenas para comprar máquinas ou pagar o salário da equipe. No entanto, nenhuma dessas situações extremas serviria. Ou ninguém operaria as máquinas por não poder pagar os salários, ou os trabalhadores não teriam as máquinas necessárias para fazer seu trabalho.

Portanto, o empresário deve se combinar da melhor maneira de trabalhar e máquinas, levando em consideração o custo a ser pago por cada um desses fatores. Para fazer isso, ele desenha uma linha isocóstica.

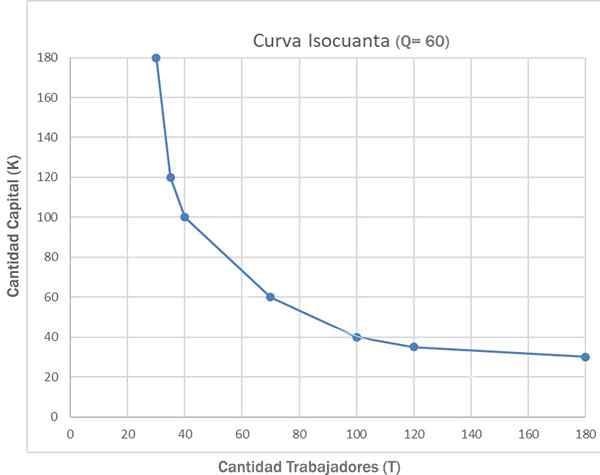
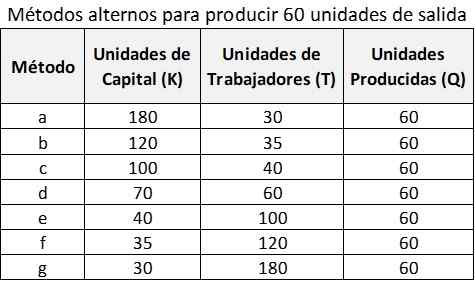
Uma curva de isocounta é uma representação gráfica das diferentes combinações de dois fatores de produção, como trabalho (t) e capital (k), que geram o mesmo nível de produção por unidade de tempo.

A saída produzida pelas diferentes combinações de T e K pode ser chamada de q, sendo uma função de T e K: q = f (t, k). A tabela a seguir mostra, com números hipotéticos, sete possíveis combinações de T e K para produzir 60 unidades de produção de Q:

Curva de Isocuanta

Essas alternativas são mostradas no gráfico a seguir, representado pela curva Q = 60. Portanto, a empresa poderia escolher a combinação c: (100k e 40t), a combinação G: (30K e 180T) ou qualquer outra combinação indicada na tabela anterior.

Uma isocounta mostra o que uma empresa quer produzir. Apresenta as seguintes propriedades:

• A curva é convexa para a origem

Isso mostra que a quantidade de capital e trabalhadores pode se substituir. No entanto, o aumento de um fator significa a diminuição do outro.

• A curva se inclina para baixo (tem uma inclinação negativa)

Isso indica que apenas a mesma quantidade pode ser produzida quando o aumento das unidades de um fator de produção é compensado com menos unidades do outro fator. Por exemplo, uma empresa pode obter o mesmo nível de produção quando o recurso de capital aumenta, mas diminuindo o recurso de trabalho.

• A curva não deve tocar o eixo y e x do gráfico

Caso contrário, a taxa de substituição técnica seria anulada, indicando que um fator de produção pode produzir a quantidade desejada sem qualquer outro fator participante.

• Você não pode atravessar as curvas um com o outro

Se vários fossem desenhados no mesmo gráfico para mostrar diferentes quantidades desejadas para produzir não puderam ser tocadas entre eles, porque indicaria que, com uma combinação dos mesmos fatores, isso ocorreria a mesma quantidade em ambos, o que é absurdo por definição.

• A forma da curva é oval

Como será visto com a linha Isochosto, é isso que ajuda a estipular a combinação de menor custo dos fatores de produção a serem usados.

Linha isocost

Você não apenas deve produzir uma certa quantidade. O empreendedor também deve ter alguma capacidade de comprar os fatores necessários para alcançar o nível de produção desejado.

Essa capacidade é mostrada com seu recurso monetário, ou seja, quanto dinheiro é capaz de gastar em capital e custos de trabalho, cujos preços são tomados como constantes. Nesse caso, o custo de capital se torna a taxa de juros bancária e a do trabalho é o salário do trabalhador.

Assim, o empresário precisa operar levando em consideração uma restrição orçamentária, que é representada pela linha Isocosto. Portanto, para encontrar a combinação de menor custo dos fatores para produzir as 60 unidades do exemplo, ele precisa construir tal isocose.

Assim, o Isochosto é uma representação gráfica que mostra as diferentes combinações que podem ser adquiridas dos fatores de produção com uma certa quantia de dinheiro. Portanto, cada ponto na linha Isochosto representa a mesma quantidade.

• Como se faz

Para delinear esta linha de isocosto, os preços de mercado desses dois fatores devem ter sido investigados. Por exemplo, suponha que o preço do capital seja de US $ 40 por unidade e o preço do trabalho seja de US $ 20 por unidade.

Assim, se o custo unitário da unidade de trabalho (t) for W = US $ 20 e o custo unitário da unidade de capital (k) é r = $ 40, então o custo total c = wt + rk.

Portanto, se um valor total estiver disponível C = $ 3.600, você pode comprar 90R+0W, 0R+180W ou outras combinações, como 50r+80w. Todas essas e outras combinações são mostradas no gráfico a seguir, usando a linha ISOCHOSTO C = $ 3.600.

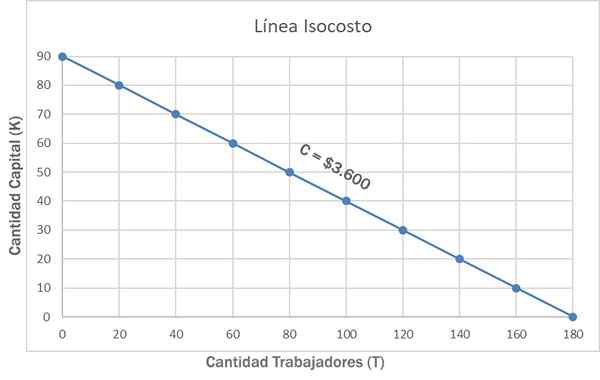
Como o preço de cada fator não varia, o Isochoxo é uma linha reta. Por outro lado, sua inclinação é negativa porque representa a relação entre o custo da mão -de -obra e do capital: w / r. É conhecido como taxa de substituição de fatores, com a qual o fator de trabalho pode ser substituído pelo fator de capital.

Minimização do custo

A empresa deve procurar minimizar o custo de produzir um certo nível de produção. Para encontrar a combinação de menor custo dos fatores para um nível de produção fixa, o gráfico da curva isocounta é combinado com o da linha Isochosto.

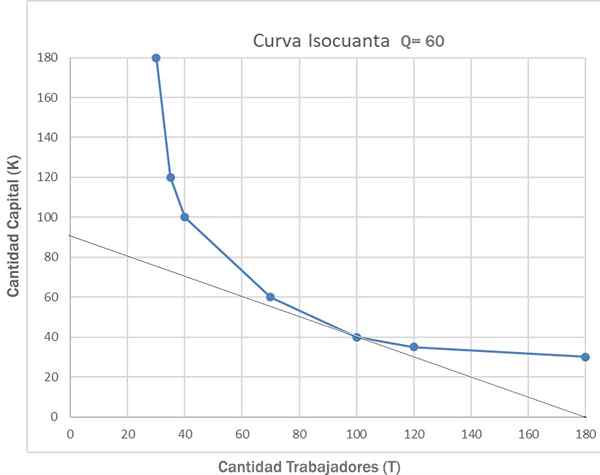
A empresa tentará encontrar a combinação de fatores mais baratos em toda a sua isocounta. Será a posição de custo mais baixo onde o isocam.

Assim, a otimização da produção é alcançada quando os preços dos fatores e a quantidade a ser produzida são iguais. Para este exemplo, o ponto de custo mínimo será a combinação "e" da tabela: k = 40 e t = 100.

Referências

1. Smriti Chand (2021). Leis de retorno: a abordagem isoquant-isocost | Economia. Sua biblioteca de artigos. Retirado de: YourAtticleLibrary.com.
2. Netescuela (2021). Isocuantas e isocostos. Retirado de: netesCuela.org.
3. Will Kenton (2020). Curva isquant. Inventopedia. Retirado de: Investopedia.com.
4. Nipun s. (2021). Linhas isoquantes e isocost (com diagrama). Discussão em economia. Retirado de: EconomicsDiscusion.líquido.
5. Wikieducator (2021). Isoquant e isocost itexon. Retirado de: Wikieducator.org.