Fórmula/coeficiente de indutância mútua, aplicações, exercícios

O indutância mútua descreve a interação entre duas bobinas futuras 1 e 2, pelas quais uma corrente variável Yo Circulando através da bobina 1, produz um fluxo de campo magnético em mudança que cruza a bobina 2.

Esse fluxo é proporcional à corrente e a constante da proporcionalidade é a indutância mútua₁₂. Ser φ_B2 O campo magnético flui através da bobina 2, então você pode escrever:

Φ_B2 = M₁₂ Yo₁

figura 1.- O transformador é a principal aplicação de indutância mútua. Fonte: Pixnio.

E se a bobina 2 tiver n₂ Voltas:

N₂ . Φ_B2 = M₁₂ Yo₁

Dessa maneira, indutância mútua ou coeficiente de indutância mútuo₁₂ Entre as duas bobinas está:

M₁₂ = N₂ . Φ_B2 / Yo₁

A indutância mútua tem Weber/Amperio ou WB/A unidades, que é chamado Henry ou Henrio e abreviado H. Portanto, 1 Henry é equivalente a 1 wb/ a.

O valor de m₁₂ Depende da geometria entre as bobinas, sua forma, seu tamanho, o número de voltas de cada uma e a distância que as separa, bem como a posição relativa entre eles.

[TOC]

Aplicações de indutância mútua

O fenômeno da indutância mútua tem muitas aplicações graças ao fato de que sua origem está na lei de Faraday-Lenz, que afirma que as correntes variáveis ​​em um circuito induzem correntes e tensões em outro, sem a necessidade de que os circuitos sejam conectados por cabos por cabos.

Quando dois circuitos interagem dessa maneira, diz -se que eles são magneticamente acoplados. Dessa maneira, a energia pode ir de um para outro, uma circunstância que pode ser usada de várias maneiras, como demonstrado por Nikola Tesla no início do século XX (ver exercício resolvido 1).

Em seus esforços para transmitir eletricidade sem cabos, Tesla experimentou com vários dispositivos. Graças às suas descobertas, o transformador foi criado, o dispositivo que passa da eletricidade das usinas para casas e indústrias.

Pode atendê -lo: vetores da unidade: características, como eliminá -lo, exemplos

O transformador

O transformador transmite tensões alternativas muito altas nas linhas elétricas, minimizando as perdas de calor e, ao mesmo tempo, fornecem energia máxima aos consumidores.

Quando a tensão atingir, eles devem ser diminuídos, o que é alcançado com o transformador. Isso consiste em duas bobinas de arame roladas em torno de um núcleo de ferro. Uma das bobinas com n₁ Turns está conectado a uma tensão alternativa e é chamado de primária. O outro, que é secundário, tem n₂ Turns, se conecta a um resistor.

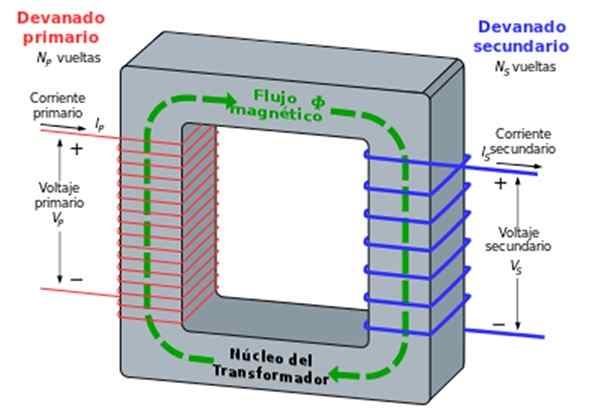Figura 2. O transformador. Fonte: Wikimedia Commons.

O núcleo de ferro garante que todas as linhas de campo magnéticas que passam por uma bobina também o façam para o outro.

A lei de Faraday estabelece que a razão entre as tensões V₂ /V₁ (secundário /primário) é igual ao motivo entre o número de voltas n₂ /N₁:

V₂ /V₁ = N₂ /N₁

Ajustando adequadamente o número de voltas, uma tensão maior ou menor que a entrada é obtida na saída.

Os transformadores são construídos de muitos tamanhos, desde enormes transformadores em instalações elétricas a carregadores de telefones celulares, laptops, mp3 e outros dispositivos eletrônicos.

Pacemaker

Os efeitos da indutância mútua também estão presentes no marcapasso para manter a frequência do batimento cardíaco, para que possa manter o fluxo sanguíneo estável.

Pacemakers trabalham com baterias. Quando estão exaustos, uma bobina externa é capaz de transmitir energia para outra bobina dentro do marcapasso. Como o procedimento é realizado por indução, não é necessário enviar o paciente a uma nova intervenção quando a bateria está esgotada.

Pode servir a você: Curva de calibração: para que é, como fazer isso, exemplos

Carregadores sem fio

Enquanto outra aplicação comum são os carregadores sem fio para diferentes objetos, como escovas de dente e telefones celulares, que são dispositivos com baixo consumo de eletricidade.

No futuro, o uso de carregadores sem fio para baterias de carro elétrico é elevado. E muitas pesquisas hoje têm como objetivo produzir eletricidade sem fio em casas. Uma das principais limitações para os momentos é a distância em que as correntes podem ser induzidas graças aos campos magnéticos.

Exercícios resolvidos

- Exercício 1

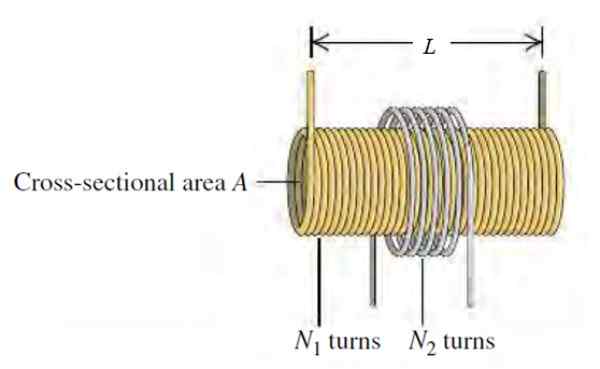
Em uma versão da bobina Tesla, usada como um gerador de alta tensão em algumas demonstrações de laboratório, há um longo comprimento L, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R₁ com n₁ redonda por unidade de comprimento, coaxialmente cercada por uma radiobina circular R₂ e n₂ rodadas.

Figura 3. Esquema de uma bobina de Tesla. Fonte: Sears Zemansky. Física da Universidade.

a) Encontre a indutância mútua m do circuito, depende da corrente que circula através do solenóide?

b) A indutância mútua depende da forma da bobina ou se suas voltas são mais ou menos roladas juntas?

Solução para

A magnitude do campo magnético do solenóide é proporcional ao número de voltas e à corrente que circula através dele, que é denotada como eu₁, Como o solenóide é o circuito 1. É dado pela expressão:

B₁ = μ_qualquerN₁.Yo₁ / EU

O fluxo do campo magnético que o solenóide cria em uma espira da bobina, que é o circuito 2, é o produto da intensidade do campo pela área ligada pelo campo:

Φ_B2 = B₁. PARA₁

Para onde₁ É a área da seção transversal do solenóide e não da bobina, uma vez que o campo solenóide é anulado fora dele:

Pode servir a você: corpos luminosos: características e como elas geram sua própria luz

PARA₁ = π (r₁)²

Substituímos a área na equação para φ_B2:

Φ_B2 = B₁. π (r₁)² = (μ_qualquerN₁.Yo₁ / EU). π (r₁)²

E a indutância mútua é dada por:

M₁₂ = N₂ . Φ_B2 / Yo₁ = N₂. [(μ_qualquerN₁.Yo₁ / EU). π (r₁)² ] / Yo₁

M₁₂ = μ_qualquer N₁ N₂ . π (r₁)² / EU

Não depende da corrente que circula através do solenóide, que vimos que é cancelado.

Solução b

Como vemos, a indutância mútua não depende da forma da bobina, nem quando as meias são apertadas. A única influência da bobina na indutância mútua é o número de voltas presentes nela, que é n₂.

- Exercício 2

Duas bobinas estão muito próximas e uma delas conduz uma corrente variável no tempo dado pela seguinte equação:

I (t) = 5.00 e ^{-0.0250 t} Sen (377 t) A

Em t = 0.800 segundos A tensão induzida na segunda bobina é medida, obtendo -3.20 v. Encontre a indutância mútua das bobinas.

Solução

Usamos a equação:

ε₂ = - m₁₂ (deu₁/dt)

Para indutância mútua entre as bobinas, simplesmente chamamos de m, pois geralmente m₁₂ = M_{vinte e um}. Precisaremos da primeira derivada da corrente em relação ao tempo:

deu₁/dt =

= - 0.0250 x 5.00 e ^{-0.0250 t} x sin (377 t) - 377 cos (377 t) x 5.00 e ^{-0.0250 t}  Ás

Avaliamos este derivado em t = 0.800 s:

deu₁/dt = - 0.0250 x 5.00 e ^{-0.0250 x 0.800} x sin (377 x 0.800) - 377 cos (377 x 0.800) x 5.00 e ^{-0.0250 x 0.800}  A/s =

= -5.00 e ^{-0.0250 x 0.800} [0.0250 x sen (377 x 0.800) + 377 cos (377 x 0.800)] =

= -1847.63 A/S

M = -3.20 v / -1847.63 a/s = 0.001732 h = 1.73 MH.

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Ciência física conceitual. 5 ª. Ed. Pearson.
3. Cavaleiro, r.  2017. Física para cientistas e engenharia: uma abordagem de estratégia. Pearson.
4. Sears, f. (2009). University Physics Vol. 2.
5. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 2. 7º. Ed. Cengage Learning.