Demonstração de identidades pitagóricas, exemplo, exercícios

São Identidades pitagóricas Todas as equações trigonométricas que são atendidas para qualquer valor do ângulo e são baseadas no teorema de Pitágoras. A mais famosa das identidades pitagóricas é a identidade trigonométrica fundamental:

Sen²(α) + cos²(α) = 1

figura 1. Identidades trigonométricas pitagóricas.

Ainda está em importância e usa a identidade pitagórica da tangente e do secante:

Então²(α) + 1 = seg²(α)

E a identidade trigonométrica pitagórica que envolve o cotangente e a colheitadeira:

1 + ctg²(α) = CSC²(α)

[TOC]

Demonstração

As razões trigonométricas seios e cosseno Eles são representados em uma circunferência de raio (1) conhecida como círculo trigonométrico. Este círculo tem um centro na origem das coordenadas ou.

Os ângulos são medidos a partir do eixo positivo do X, por exemplo, o ângulo α na Figura 2 (ver posteriormente). Ao contrário das mãos do relógio se o ângulo for positivo e na direção das mãos, se for um ângulo negativo.

O semi -direito com origem ou ângulo α é desenhado, que intercepta o círculo unitário no ponto P. O ponto P é projetado ortogonalmente no eixo horizontal x dando origem ao ponto C. Da mesma forma, P é projetado perpendicularmente no eixo vertical e dando origem ao ponto S.

Você tem o triângulo OCP certo em c. 

O peito e o cosseno

Deve -se lembrar que a razão trigonométrica seios É definido em um triângulo direito da seguinte forma:

O seio de um ângulo do triângulo é a proporção ou razão entre o Cateto oposto ao ângulo e a hipotenusa do triângulo.

Aplicado ao triângulo OCP da Figura 2 seria assim:

Sin (α) = cp / op

Mas CP = OS e OP = 1, para que:

Sin (α) = os

O que significa que a projeção no eixo y tem um valor igual ao seio do ângulo mostrado. Deve -se notar que o valor máximo da mama de um ângulo (+1) ocorre quando α = 90º e o mínimo (-1) quando α = -90º ou α = 270º.

Pode servir a você: espaço vetorial: base e dimensão, axiomas, propriedades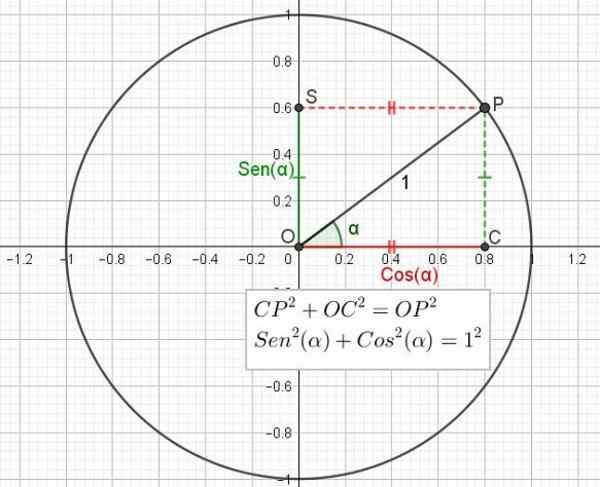Figura 2. Círculo trigonométrico mostrando a relação entre o teorema de Pitágoras e a identidade trigonométrica fundamental. (Elaboração própria)

Da mesma forma, o cosseno de um ângulo é a razão entre a categoria adjacente ao ângulo e a hipotenusa do triângulo.

Aplicado ao triângulo OCP da Figura 2 seria assim:

Cos (α) = oc / op

Mas op = 1, para que:

Cos (α) = oc

O que significa que a projeção de OC no eixo x tem um valor igual ao do seio do ângulo mostrado. Deve-se notar que o valor máximo do cosseno (+1) ocorre quando α = 0º ou α = 360º, enquanto o valor mínimo do cosseno é (-1) quando α = 180º.

A identidade fundamental

Para o retangular OCP Triangle, o teorema de Pitágoras é aplicado, que afirma que a soma do quadrado das categorias é igual ao quadrado da hipotenusa:

Cp² + Oc² = Op²

Mas já foi dito que Cp = os = sin (α), que oc = cos (α) e que op = 1, para que a expressão anterior possa ser reescrita, dependendo do seio e do cosseno do ângulo:

Sen²(α) + cos²(α) = 1

O eixo tangente

Assim como o eixo X no círculo trigonométrico é o eixo do cosseno e do eixo e o eixo da mama, da mesma maneira que há o eixo da tangente (veja a Figura 3), que é precisamente a linha tangente à unidade círculo no ponto na coordenada do ponto B (1, 0). 

Se você quiser saber o valor da tangente de um ângulo, o ângulo é extraído do eixo positivo do x, a interseção do ângulo com o eixo da tangente define um ponto q, o comprimento do segmento de OQ é a tangente do ângulo.

Pode atendê -lo: derivados algébricos

Isso ocorre porque, por definição. Ou seja, (α) = qb / ob = qb / 1 = qb.

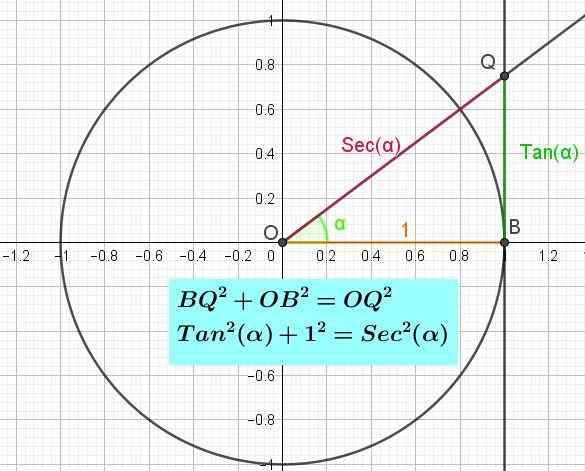Figura 3. O círculo trigonométrico mostrando o eixo da tangente e a identidade pitagórica da tangente. (Elaboração própria)

A identidade pitagórica da tangente

A identidade pitagórica da tangente pode ser demonstrada se o triângulo retângulo em B (Figura 3) for considerado (Figura 3). Aplicando o teorema de Pitágoras ao referido triângulo, você tem que BQ² + Ob² = Oq². Mas já foi dito que BQ = tan (α), que ob = 1 e que oq = s (α), de modo que a substituição da igualdade de pitágoras pelo triângulo correto obq que possui:

Então²(α) + 1 = seg²(α).

Exemplo

Verifique se as identidades pitagóricas são ou não atendidas no triângulo retângulo de catetos AB = 4 e BC = 3.

Solução: As categorias são conhecidas, é necessário determinar a hipotenusa, que é:

Ac = √ (ab^2 + bc^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

O ângulo ∡bac será chamado α, ∡bac = α. Agora os motivos trigonométricos são determinados:

Sin α = bc / ac = 3/5 

Cos α = ab / ac = 4/5 

Tan α = BC / AB = 3/4 

Cotan α = ab / bc = 4/3 

Sec α = AC / AB = 5/4 

CSC α = AC / BC = 5/3

Começa com a identidade trigonométrica fundamental:

Sen²(α) + cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Conclui -se que é cumprido.

- A próxima identidade pitagórica é a da tangente:

Então²(α) + 1 = seg²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

E conclui -se que a identidade da tangente é verificada.

- Da mesma forma, o do cotangente:

Pode atendê -lo: seleções aleatórias com ou sem substituição

1 + ctg²(α) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Conclui -se que também é cumprido, o que concluiu a tarefa de verificar as identidades pitagóricas para o triângulo dado.

Exercícios resolvidos

Teste as seguintes identidades, com base nas definições de razões trigonométricas e identidades pytagóricas.

Exercício 1

Prove o que cos² x = (1 + sen x) (1 - sin x).

Solução: O membro certo reconhece o produto notável da multiplicação de um binomial por seu conjugado que, como é conhecido, é uma diferença de quadrados:

Cos² x = 1² - Sen² x

Então o termo com o peito no lado direito passa para o lado esquerdo com o sinal alterado:

Cos² X + sen² x = 1

Observando que a identidade trigonométrica fundamental foi alcançada, conclui -se que a expressão dada é uma identidade, ou seja, é cumprida para qualquer valor de x.

Exercício 2

A partir da identidade trigonométrica fundamental e usando as definições de razões trigonométricas para demonstrar a identidade pitagórica da colheitadeira.

Solução: A identidade fundamental é:

Sen²(x) + cos²(x) = 1

Ambos os membros estão divididos entre sen²(x) e o denominador é distribuído no primeiro membro:

Sen²(x)/pecado²(x) + cos²(x)/pecado²(x) = 1/sen²(x)

É simplificado:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cotan (x) é uma identidade (não -fagórica) que é verificada pela definição de razões trigonométricas. Da mesma forma, ocorre com a seguinte identidade: 1/sin (x) = csc (x).

Finalmente você tem que:

1 + ctg²(x) = CSC²(x)

Referências

1. Baldor J. (1973). Geometria plana e espaço com uma introdução à trigonometria. Cultural da América Central. C.PARA.
2. C. E. PARA. (2003). Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
3. Campos, f., CERECEDO, f. J. (2014). Matemática 2. Grupo editorial da Patria.
4. Iger. (s.F.). Matemática Primeiro Semestre Tacaná. Iger.
5. Jr. Geometria. (2014). Polígonos. Lulu Press, Inc.
6. Miller, Heeren e Hornsby. (2006). Matemática: Raciocínio e Aplicações (Décima Edição). Pearson Education.
7. Patiño, m. (2006). Matemática 5. Editorial Progreso.
8. Wikipedia. Identidades e fórmulas de trigonometria. Recuperado de: é.Wikipedia.com