Icosagono

O que é um icogon?

A Icosagono ou isodecagon É um polígono que tem 20 lados. Um polígono é uma figura plana formada por uma sequência finita de segmentos de linha (mais de dois), que incluem uma região do plano.

Cada segmento de linha é chamado de lado e a interseção de cada par de lados é chamada de vértice. De acordo com o número de lados, os polígonos recebem nomes específicos.

Os mais comuns são o triângulo, quadrilateral, Pentágono e hexágono, que têm 3, 4, 5 e 6 lados, respectivamente, mas podem ser construídos com o número de lados desejados.

Características de um icogon

Abaixo estão algumas características dos polígonos e sua aplicação em um icogon.

1- classificação

Um icosgono, sendo um polígono, pode ser classificado como regular e irregular, onde a palavra regular refere -se ao fato de que todos os lados têm o mesmo comprimento e ângulos internos medem da mesma forma; Caso contrário, diz -se que o icosão (polígono) é irregular.

2- isodecágono

O Icosgon comum também é chamado de isodogona regular, porque para obter um icosgon regular -GOUGE O que deve ser feito é bisecar (divida em duas partes iguais) cada lado de um decágono regular (10 lados polígono).

3- perímetro

Para calcular o perímetro "P" de um polígono comum, o número de lados é multiplicado pelo comprimento de cada lado.

No caso particular de um icogon, o perímetro é igual a 20xl, onde "L" é o comprimento de cada lado.

Por exemplo, se você tem um icosão de 3 cm regular, seu perímetro é igual a 20x3cm = 60 cm.

Está claro que, se o isocágono for irregular, a fórmula anterior não pode ser aplicada.

Nesse caso, os 20 lados devem ser adicionados separadamente para obter o perímetro, ou seja, o perímetro “P” é igual a ∑Li, com i = 1,2,…, 20.

4- Diagonal

O número de diagonais "d" que possui um polígono é igual a n (n-3)/2, onde n representa o número de lados.

No caso de um icogon, deve ser d = 20x (17)/2 = 170 diagonais.

5- Soma dos ângulos internos

Há uma fórmula que ajuda a calcular a soma dos ângulos internos de um polígono comum, que pode ser aplicado a um icoSgon comum.

A fórmula consiste em subtrair 2 ao número de lados do polígono e depois multiplicar esse número por 180º.

A maneira como essa fórmula é obtida é que podemos dividir um polígono de n lados em triângulos N-2 e usando o fato de que a soma dos ângulos internos de um triângulo é 180º, a fórmula é obtida.

Na imagem a seguir, a fórmula para um Enegon regular (polígono de 9 anos) é ilustrado.

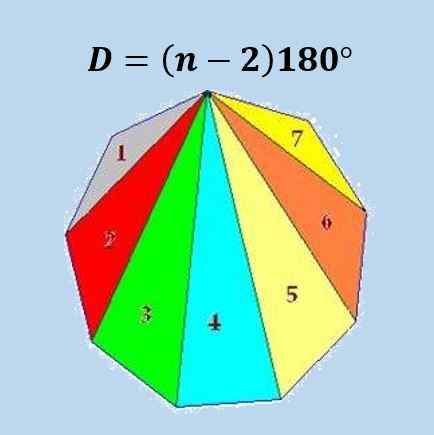
Usando a fórmula anterior, obtém -se que a soma dos ângulos internos de qualquer icosagon é 18 × 180º = 3240º ou 18π.

6- área

Para calcular a área de um polígono comum, é muito útil conhecer o conceito de apoteme. O apoteme é uma linha perpendicular que vai do centro do polígono comum até o ponto médio de qualquer um de seus lados.

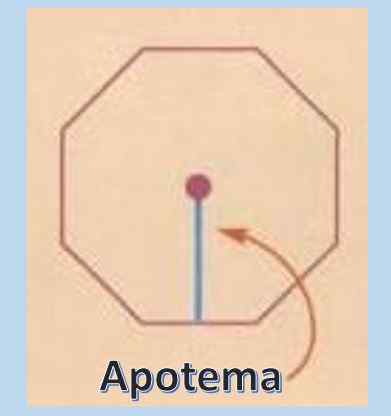
Uma vez que o comprimento do apoteme é conhecido, a área de um polígono comum é a = pXA/2, onde "p" representa o perímetro e "a" o apoteme.

No caso de um icosão regular que você tem na sua área, é a = 20xlxa/2 = 10xlxa, onde "l" é o comprimento de cada lado e "a" seu apoteme.

Por outro lado, se você tiver um polígono irregular de N lados, para calcular sua área, o polígono é dividido em triângulos conhecidos N-2, então a área de cada um desses triângulos N-2 é calculada e, finalmente, todos esses são áreas adicionadas.

O método descrito acima é conhecido como triangulação de um polígono.

Referências

1. Elementos de geometria: com numerosos exercícios e geometria da bússola. Universidade de Medellin.
2. Iger. (s.F.). Matemática Primeiro Semestre Tacaná. Iger.