Homotecia

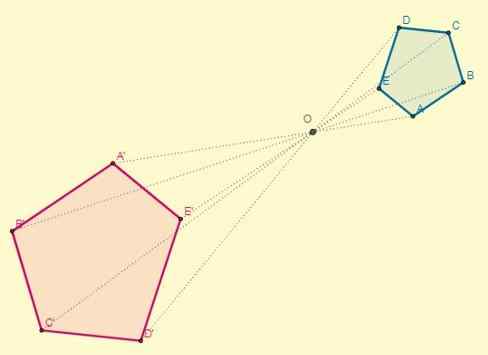
O Homotecia É uma mudança geométrica no avião onde, de um ponto fixo chamado centro (O), as distâncias são multiplicadas por um fator comum. Dessa maneira, cada ponto P corresponde a outro ponto da transformação, e estes estão alinhados com o ponto ou.

Então, a homotecia é uma correspondência entre duas figuras geométricas, onde os pontos transformados são chamados de homotéticos, e estes estão alinhados com um ponto fixo e com segmentos paralelos entre si.

Explicação e fórmula

A homotecia é uma transformação que não tem uma imagem congruente, porque, de uma figura, eles obterão uma ou mais figuras de tamanho maior ou menor que a figura original; isto é, homotecia transforma um polígono em outro semelhante.

Para que a homotecia seja cumprida, o ponto a ponto e a linha reta deve corresponder, para que casais de pontos homólogos estejam alinhados com um terceiro ponto fixo, que é o centro de homotecia.

Da mesma forma, os pares de linhas que se unem devem ser paralelos. A relação entre tais segmentos é uma constante chamada homotecia (k) razão; De tal maneira que a homotecia pode ser definida como:

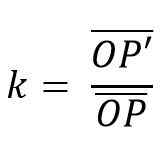
Para fazer esse tipo de transformação, começa um ponto arbitrário, que será o centro da homotecia.

A partir deste ponto, segmentos de linha são desenhados para cada vértice da figura ser transformado. A escala em que a reprodução da nova figura é feita é dada pelo motivo da homotecia (k).

Propriedades de homotecia

Uma das principais propriedades da homotecia é que, pelo motivo da homotecia (k), todas as figuras homotéticas são semelhantes. Entre outras propriedades excelentes estão as seguintes:

Pode atendê -lo: proporcionalidade composta: explicação, regra de três compostos, exercícios

- O Homotecia Center (O) é o único ponto duplo e se transforma; isto é, não varia.

- As linhas que passam pelo centro se tornam elas mesmas (elas são duplas), mas os pontos que o compõem não são duplos.

- As linhas que não passam pelo centro são transformadas em linhas paralelas; Dessa forma, os ângulos de homotecia permanecem iguais.

- A imagem de um segmento por uma homotecia central ou e a razão k é um segmento paralelo e tem K vezes o seu comprimento. Por exemplo, como visto na imagem a seguir, um segmento AB para homotecia será outro segmento A'B ', para que o AB seja paralelo a A'B' e o K será:

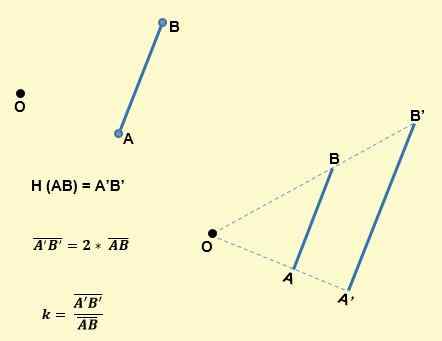
- Ângulos homotéticos são congruentes; isto é, eles têm a mesma medida. Portanto, a imagem de um ângulo é um ângulo que tem a mesma amplitude.

Por outro lado, a homotecia deve variar dependendo do valor de sua razão (k), e os seguintes casos podem ocorrer:

- Se a constante k = 1, todos os pontos são fixos porque se transformam. Assim, a figura homotética coincide com o original e a transformação será chamada de função de identidade.

- Se k ≠ 1, o único ponto fixo será o centro da homotecia (O).

- Se k = -1, homotecia se tornará uma simetria central (c); Isto é, uma rotação ocorrerá em torno de C, em um ângulo de 180^qualquer.

- Se k> 1, o tamanho da figura transformada será maior para o tamanho do original.

Pode atendê -lo: números irracionais: história, propriedades, classificação, exemplos

- Sim 0 < k < 1, el tamaño de la figura transformada será menor que el de la original.

- Sim -1 < k < 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.

- Sim k < -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.

Tipos de homotecia

A homotecia também pode ser classificada em dois tipos, dependendo do valor de sua razão (k):

Homotecia direta

Ocorre se a constante k> 0; Ou seja, os pontos homotéticos estão do mesmo lado em relação ao centro:

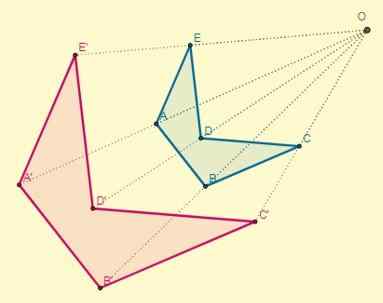
O fator de proporcionalidade ou razão de similaridade entre figuras homotéticas diretas sempre será positivo.

Homotecia inversa

Ocorre se a constante k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:

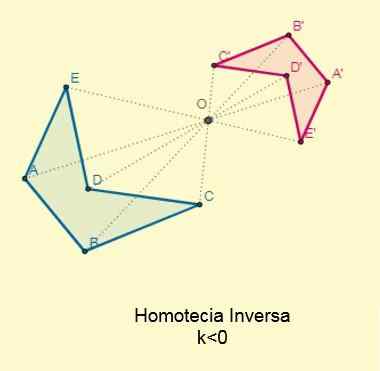
O fator de proporcionalidade ou razão de similaridade entre as figuras homotéticas inversas sempre será negativo.

Composição

Quando vários movimentos são realizados sucessivamente até uma figura igual ao original, uma composição de movimentos ocorre. A composição de vários movimentos também é um movimento.

A composição entre duas homotecia resulta em uma nova homotecia; Ou seja, existe um produto de homotecia no qual o centro estará alinhado com o centro das duas transformações originais, e a razão (k) é o produto das duas razões pelas quais.

Assim, na composição de duas homoties h₁(QUALQUER₁, k₁) e h₂(QUALQUER₂, k₂), A multiplicação de suas razões: k₁ x k₂ = 1 resultará em uma homotecia da razão k₃ = K₁ x k₂. O centro desta nova homotecia (ou₃) estará localizado na linha ou₁ QUALQUER₂.

Pode atendê -lo: ângulos opostos pelo vértice (com um exercício resolvido)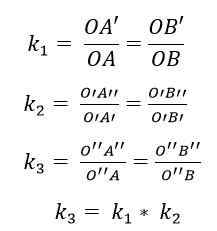

Homotecia corresponde a uma mudança plana e irreversível; Se duas homotecia se aplicarem que tenham o mesmo centro e razão, mas com um sinal diferente, a figura original será obtida.

Exemplos de homotecia

1. Primeiro exemplo

Aplique uma homotecia ao polígono dado do centro (O), localizado a 5 cm do ponto A e cuja razão é k = 0,7.

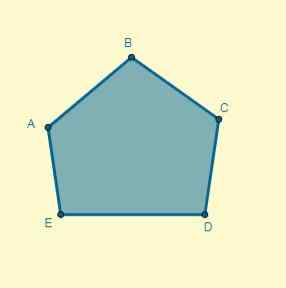
Solução

Qualquer ponto é escolhido como o centro da homotecia e, a partir disso, eles são negociados pelos vértices da figura:

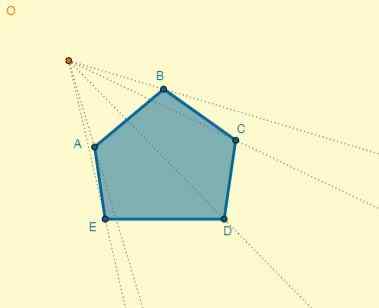
A distância do centro (O) ao ponto A é OA = 5; Com isso, você pode determinar a distância de um dos pontos homotéticos (OA ') também sabendo que k = 0,7:

Oa '= k x oa.

Oa '= 0,7 x 5 = 3,5.

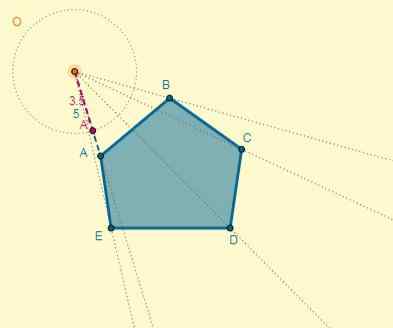
O processo pode ser feito para cada vértice, ou você também pode desenhar o políticos homotético, lembrando que os dois polígonos têm lados paralelos:

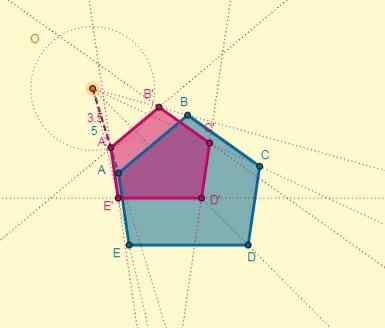
Finalmente, a transformação é vista da seguinte maneira:

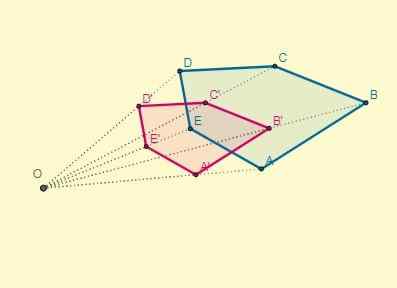
2. Segundo exemplo

Aplique uma homotecia ao polígono dado do Center (O), localizado 8,5 cm do ponto C e cuja razão k = -2.

Solução

A distância do centro (O) ao ponto C é OC = 8,5; Com esses dados, é possível determinar a distância de um dos pontos homotéticos (OC '), também sabendo que k = -2:

Oc '= k x oc.

Oc '= -2 x 8.5 = -17

Depois de desenhar os segmentos dos vértices do polígono transformado, os pontos iniciais e seus homotéticos estão localizados nas extremidades opostas em relação ao centro: