Matemática

Hipérbole

737
133
Shawn Leffler

O que é uma hipérbole?

A hipérbole é o conjunto de pontos do avião, de modo que o valor absoluto da diferença entre as distâncias para dois pontos fixos, chamados holofotes, permanece constante. Este conjunto de pontos forma a curva com dois ramos observados na Figura 1.

Há um ponto P (x, y), o foci f₁ e f₂ separou uma distância igual a 2C. A maneira matemática de expressar esse relacionamento é através:

$\left |d__P_1-d__P_2 \right |=constante$

figura 1. Hiperblo com eixo focal horizontal. Fonte: f. Zapata.

Todos os pontos da hipérbole satisfaz. O ponto médio entre os holofotes é chamado Centro C e na figura que coincide com o ponto (0,0), mas a hipérbole também pode ser deslocada e seu centro corresponde a outro ponto de coordenada C (H, K).

Na figura superior, o eixo x é o eixo focal da hipérbole, pois existem os holofotes, mas você também pode construir um cujo eixo focal é o eixo e o eixo.

A hiperbola faz parte das curvas conhecidas como cônico, Eles são chamados assim porque podem ser derivados do corte de um cone com uma seção plana. Uma hipérbole é obtida ao cruzar o cone e o avião, desde que ele não passe pelo vértice do cone e o ângulo que forma o plano com o eixo do cone é menor que o que se forma com o eixo de Geratrix do mesmo.

Juntamente com a parábola, circunferência e elipse, os cônicos são conhecidos desde os tempos antigos. O matemático grego Apollonius de Perga (262-190 aC) escreveu um tratado de geometria onde ele detalhou suas propriedades e ele próprio deu a eles os nomes com os quais eles se conhecem até hoje.

Características da hipérbole

Essas são algumas das características mais destacadas de uma hipérbole:

É uma curva plana, portanto é suficiente para dar as coordenadas (x, y) de cada ponto que pertence a ele.
É também uma curva aberta, diferente da circunferência ou elipse.
Tem dois ramos organizados simetricamente.
Tanto o eixo vertical quanto o eixo horizontal podem ser considerados eixos de simetria, mas o eixo onde os holofotes são chamados eixo focal ou eixo principal.
É simétrico em relação ao seu centro.
A hiperblo cruza o eixo focal em dois pontos chamados Vértices, É por isso que o eixo focal às vezes é chamado eixo real, Enquanto o outro eixo é chamado Eixo imaginário, Porque não tem pontos em comum com a hipérbole.
O centro da hipérbole está localizado a meio caminho entre os pontos chamados focos.
Está associado a duas linhas muito particulares chamadas assíntotas, que são linhas para as quais a hipérbole se aproxima, mas sem cruzá -las, quando os valores de x e y são muito grandes. As assíntotas se cruzam no centro da hipérbole.

Pode atendê -lo: função superjectiva: definição, propriedades, exemplos

Equações e fórmulas

Equação de Hiperbol com o centro em (0,0)

A partir da definição dada no início:

$\left |d__P_1-d__P_2 \right |=constante$

Para essa constante positiva, geralmente é chamado 2a e é a distância que separa os vértices da hipérbole, então:

$\left |d__P_1-d__P_2 \right |=2a$

Por outro lado, DP₁, Dp₂ e 2C são os lados do triângulo mostrados na Figura 1 e, pela geometria elementar, a subtração dos quadrados dos lados de qualquer triângulo é sempre menor que o quadrado do lado restante. Então:

4º²< 4c²

para < c

Este resultado será útil em breve.

Como a distância entre dois pontos P₁(x₁,e₁) E P₂(x₂,e₂) é:

$d_12=\sqrt(x_2-x_1)^2+(y_2-y_1)^2$

Substituindo as coordenadas p (x, y), f₁(-C, 0) e f₂(C, 0) permanece:

$\left |d_P_1-d_P_2 \right |=\left |\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2 \right |=2a$

Que é equivalente a:

$\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2=\pm 2a$

Quadrado nos dois membros para eliminar as raízes e reorganizar os termos que você atinge:

$\left (c^2-a^2 \right )x^2-a^2 y^2 =\left (c^2-a^2 \right )a^2$

Para a quantidade c² - para², o que é sempre uma quantidade positiva porque < c, se la denomina b², Portanto, o acima é reescrito como:

b²x² - para²e² = a² b²

Dividindo todos os termos por² b², É a equação de hiperbola centrada (0,0) com o eixo real horizontal:

$\fracx^2a^^2-\fracy^2b^^2=1$

Com A e B maior que 0. Esta equação é chamada Equação canônica de Hyerbola e o denominador para² Sempre corresponde à fração positiva.

A hiperbola centrou -se (0,0) e com o eixo real vertical assume o formulário:

$\fracy^^2a^2-\fracx^^2b^2=1$ Interseções da hipérbole com os eixos de coordenadas

As interseções da hipérbole com os eixos de coordenadas estão sendo feitas, respectivamente, y = 0 e x = 0 na equação:

Para y = 0

x² /para² = 1 ⇒ x² = a²

x = ± A

A hipérbole corta no eixo x em dois pontos chamados vértices, cujas respectivas coordenadas x são: x = a y x = -a

Para x = 0

É obtido -e² /b² = 1, que não tem solução real e segue que a hipérbole não corta para o eixo vertical.

Equação de Hyperbola com o centro em (H, K)

Se o centro da hipérbole estiver no ponto C (h, k), então sua equação canônica é:

$\frac\left (x-h \right )^2a^^2-\frac\left (y-k \right )^2b^^2=1$

Elementos de hiperbola

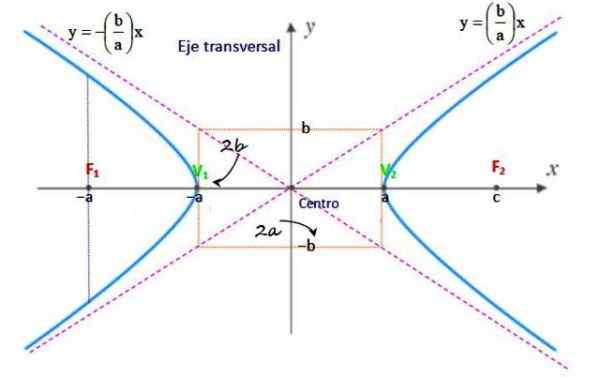Figura 2. Elementos de hiperbola. Fonte: f. Zapata.

Centro

É o ponto médio do segmento f₁F₂E suas coordenadas são (h, k) ou (x_qualquer,e_qualquer).

Pode atendê -lo: divisão sintética

Focos

Eles são os dois pontos fixos f₁ e f₂ que estão no eixo real da hipérbole, com relação à qual a diferença de distâncias para o ponto p (x, y) permanece constante. A distância entre os holofotes e o centro da hipérbole é "C".

Rádio vetorial

Isso é chamado de distância entre um ponto P e um dos holofotes.

Distância focal

É a distância que separa os dois holofotes e é equivalente a 2C.

Vértices

Os vértices v₁ e V₂ Eles são os pontos em que a hipérbole cruza o eixo real. Um vértice e o centro da hipérbole são separados pela distância A, portanto, a distância entre os vértices é 2a.

Eixo focal, eixo principal ou eixo real

É o eixo onde os holofotes estão localizados e mede 2C. Ele pode estar localizado em qualquer um dos dois eixos cartesianos e a hipérbole o cruza nos pontos chamados vértices.

Eixo transversal, eixo secundário ou eixo imaginário

É o eixo perpendicular ao eixo focal e mede 2b. A hipérbole não o intercepta, por isso também é chamado de eixo imaginário.

Assíntotas

São duas linhas, cujos respectivos pendentes são M₁ = (b/a) e m₂ = - (b/a), que são destinados ao centro da hipérbole. A curva nunca cruza essas linhas e o produto entre as distâncias de qualquer ponto da hipérbole para as assíntotas, é constante.

Para encontrar as equações das assíntotas, basta combinar o lado esquerdo da equação canônica de Hyperblo a 0. Por exemplo, para a hiperbola centrada na origem:

$\fracx^^2a^2-\fracy^^2b^2=0\Rightarrow \fracy^^2b^2=\fracx^^2a^2$

Retângulo Hyberbola

É o retângulo cuja largura é a distância entre os vértices 2a e a distância 2b e está focada no centro da hipérbole. Sua construção facilita o layout manual da hipérbole.

Lado reto

Corda que passa por um dos holofotes, perpendicular ao eixo real.

Excentricidade

É definido como o quociente entre a distância focal e o eixo real:

E = c/a

É sempre maior que 1, pois C é maior que a e menor que √2.

O valor e indica se a hipérbole é bastante fechada (retângulo estreito, alongado na direção do eixo principal) ou aberto (retângulo largo, alongado na direção do eixo imaginário).

Tangente reta à hipérbole no ponto P (x₁,e₁)

Uma linha tangente para a hipérbole em um ponto P (x₁,e₁) É o bissetor dos dois vetores de rádios daquele ponto.

Para uma hipérbole com o eixo principal paralelo ao eixo x, a inclinação da linha tangente à hipérbole em um ponto P (x₁,e₁) É dado por:

Pode atendê -lo: operações combinadas

$m=\left (\fracba \right )^2\left (\fracx_1y_1 \right )$

E se a hipérbole for o eixo principal paralelo ao eixo y, então:

$m=\left (\fracab \right )^2\left (\fracx_1y_1 \right )$

Exemplos de hipérbole

Dispersão de partículas alfa por um núcleo

Ao bombardear núcleos atômicos com partículas alfa, que nada mais são do que os núcleos de hélio, estes são repelidos, uma vez que qualquer núcleo atômico tem uma carga positiva. Esses núcleos de hélio são dispersos seguindo trajetórias hiperbólicas.

Trajetórias dos corpos do sistema solar

Figura 3: Planetas de sistema solar

No sistema solar, os objetos se movem sob a ação da força da gravidade. A descrição do movimento deriva de uma equação diferencial na qual a força é conservadora e inversamente proporcional ao quadrado da distância. E as soluções desta equação são as possíveis trajetórias que seguem os objetos.

Bem, essas trajetórias são sempre cônicas: circunferências, elipses, parábolas ou hiperbolas. Os dois primeiros são curvas fechadas, e é assim que os planetas se movem, mas alguns cometas ainda são trajetórias abertas, como parábolas ou hiperbolas, com o sol localizado em um dos holofotes.

Som mínimo

Quando há duas fontes de som, como dois alto -falantes que emitem sons uniformemente em todas as direções, localizadas ao longo de uma linha reta, os mínimos de intensidade sonora (interferência destrutiva) estão em uma hiperbola cujo eixo principal é dita linha e nos holofotes de A hipérbole são os alto -falantes.

Exercício resolvido

Encontre os elementos da seguinte hipérbola: vértices, focos e assíntotas da hipérbole e construa seu gráfico:

$\fracx^^216-\fracy^^24=1$

Solução

O centro desta hipérbole coincide com a origem das coordenadas e seu eixo real é horizontal, uma vez que a fração positiva corresponde à variável x.

Os semi -eixos de hiperbola são:

para² = 16 ⇒ a = 4

b² = 4 ⇒ b = 2

Dessa forma, o retângulo central mede 4 unidades de largura e 2 unidades de altura. Lembrando que foi mencionado acima que C² - para²= b², então:

c² = a²+ b² ⇒ c² = 16 + 4 = 20

Portanto, o semi-de-de-de-de-ano é:

C = √20 = 2√5

E os focos estão em pontos de coordenadas f₁ (-2√5.0) e f₂ (2√5.0).

As encostas das assíntotas são:

M = ± (B/A) = ± (2/4) = ± 0.5

Portanto, as respectivas equações de cada um são:

e₁ = 0.5x; e₂ = -0.5x

Hyperblo pode facilmente gravar graficamente através de software on -line como Geogebra:

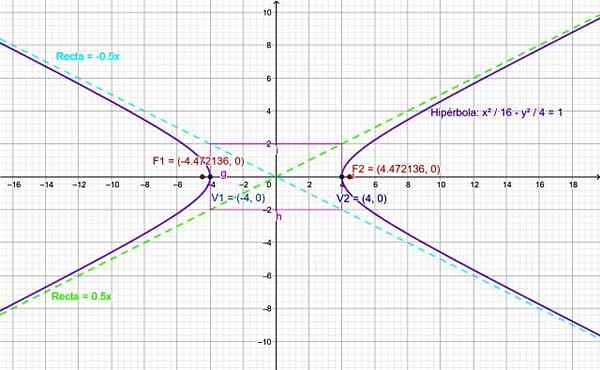Figura 4. Gráfico para a hipérbole do exercício resolvido. Fonte: f. Zapata.

Referências