Definição de Hypercubo, dimensões, coordenadas, desdobrado

A Hipercubo é um cubo de dimensão n. O caso particular de dimensão hipercubo é chamado Testeract. Um hipercubo ou n-cubo consiste em segmentos retos, todo o mesmo comprimento que são ortogonais em seus vértices.

Os seres humanos percebem o espaço tridimensional: largo, alto e profundidade, mas não é possível visualizar um hipercubo de dimensão maior que 3. 

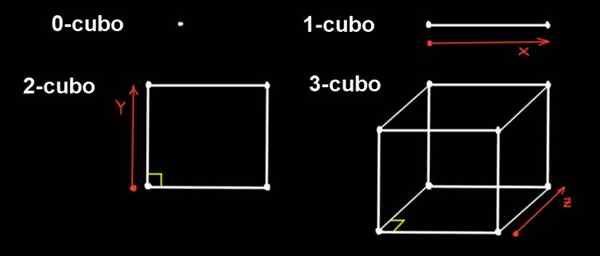
figura 1. Um 0-cubo é um ponto, se esse ponto se estender em uma direção a uma distância de uma maneira 1 cubo, se esse 1 cubo se estender uma distância até a direção ortogonal, há um 2 cubo (de lados a x a), Se o 2 cubo se estender uma distância na direção ortogonal, há um 3 cubo. Fonte: f. Zapata.

Podemos fazer projeções no espaço tridimensional para representá -lo, semelhante à maneira como projetamos um cubo em um avião para representá -lo.

Na dimensão 0, o único número é o ponto, então um 0 cubo é um ponto. Um 1 cubo é um segmento reto, que é formado movendo um ponto à distância.

Para sua parte, um 2 cubo é um quadrado. Ele é construído deslocando o 1 cubo (o segmento a longo) na direção e, que é ortogonal ao endereço X, uma distância de.

O 3 cubo é o cubo comum. É construído a partir do quadrado que desloca o mesmo na terceira direção (z), que é ortogonal para as direções x e y, uma distância para.

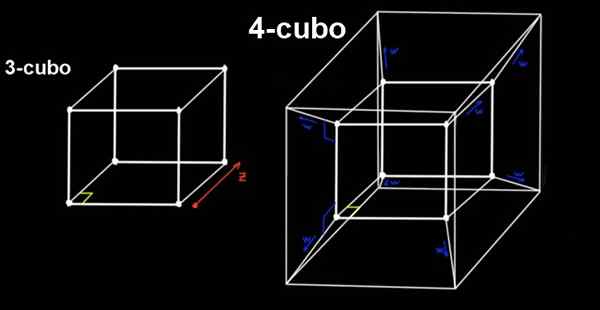Figura 2. Um 4 cubo (testerato) é a extensão de um 3 cubo na direção ortogonal para os três endereços espaciais convencionais. Fonte: f. Zapata.

O 4 cubo é o julgamento, que é construído a partir de um 3 cubo, deslocando o mesmo ortogonalmente, uma distância para, em direção a uma quarta dimensão (ou quarta direção), que não podemos perceber.

Um gatilho tem todos os seus ângulos retos, tem 16 vértices e todas as suas bordas (18 no total) têm o mesmo comprimento para.

Se o comprimento das bordas de um n-cubo ou hipercubo da dimensão n for 1, é um hipercubo unitário, no qual as medidas diagonais mais longas √n.

Pode servir a você: Programação linear: para que serve, modelos, restrições, aplicaçõesFigura 3. Um n-cubo é obtido de um (n-1)-cubo, estendendo-o ortogonalmente na próxima dimensão. Fonte: Wikimedia Commons.

[TOC]

Quais são as dimensões?

As dimensões são os graus de liberdade, ou as possíveis direções em que um objeto pode se mover.

Na dimensão 0, não há possibilidade de se mover e o único objeto geométrico possível é o ponto.

Uma dimensão no espaço euclidiano é representada por uma linha ou eixo orientado que define essa dimensão, chamada de eixo x. A separação entre dois pontos A e B é a distância euclidiana:

D = √ [(x_para - x_b)²]. 

Em duas dimensões, o espaço é representado por duas linhas ortogonais orientadas entre si, chamadas x e eixo.

A posição de qualquer ponto nesse espaço bilimensional é dada por seu par de coordenadas cartesianas (x, y) e a distância entre dois pontos A e B, qualquer um será:

D = √ [(x_para - x_b)² + (e_para - e_b)²]

Porque é um espaço onde a geometria euclida é cumprida.

O espaço tridimensional

Espaço tridimensional é o espaço em que nos movemos. Tem três direções: largura, alta e profundidade.

Em uma sala vazia, os cantos perpendiculares uns com os outros dão essas três direções e a cada um, podemos associar um eixo: x, y, z, z,.

Este espaço também é euclidiano e a distância entre dois pontos A e B é calculada da seguinte forma:

D = √ [(x_para - x_b)² + (e_para - e_b)² + (Z_para - z_b)²]

Os seres humanos não podem perceber mais de três dimensões espaciais (ou euclídeos).

No entanto, do ponto de vista estritamente matemático, é possível.

Neste espaço, um ponto tem coordenadas: (x1, x2, x3, ..., xn) e a distância entre dois pontos é: 

D = √ [(x_1º - x_{1 b})² + (x_2º - x_2b)² +... + (x_{n / D} - x_Nb)²].

Pode servir a você: distribuição hipergeométrica: fórmulas, equações, modelo

A quarta dimensão e tempo

De fato, em teoria do tempo de relatividade é tratado como mais uma dimensão e uma coordenada está associada.

Mas deve -se esclarecer que essa coordenada associada ao tempo é um número imaginário. Portanto, a separação de dois pontos ou eventos no espaço-tempo não é euclidiana, mas segue a métrica de Lorentz.

Um hipercubo quadridimensional (o gatilho) não vive no espaço-tempo, pertence a um hiper-espaço euclideal quadridimensional. 

Figura 4. Projeção 3D de um hipercubo quatro dimensional em rotação simples em torno de um avião que divide a figura frontal à esquerda, de volta para a direita e de cima para baixo. Fonte: Wikimedia Commons.

As coordenadas de um hipercubo

As coordenadas dos vértices de um n-cubo centralizado na origem são alcançados fazendo todas as permutações possíveis da seguinte expressão:

(A/2) (± 1, ± 1, ± 1, .. ., ± 1)

Onde a é o comprimento da borda.

-Ele volume De uma borda da borda A é: (a/2)ⁿ (2ⁿ) = aⁿ.

-O Diagonal mais longo É a distância entre vértices opostos.

-Os seguintes são vértices opostos em um quadrado: (-1, -1) e (+1, +1).

-E em um Cubo: (-1, -1, -1) e (+1, +1, +1). 

-O Diagonal mais longo de uma medidas n-cubo: 

D = √ [1 -(-1))² +… + (1 -(-1))²] = √ [n 2²] = 2√n

Nesse caso, assumiu -se que o lado é a = 2. Para um lado n-cubo para qualquer um permanecerá:

d = a√n.

-Um teste tem cada um de seus 16 vértices conectados a quatro bordas. A figura a seguir mostra como os vértices estão conectados em um gatilho.

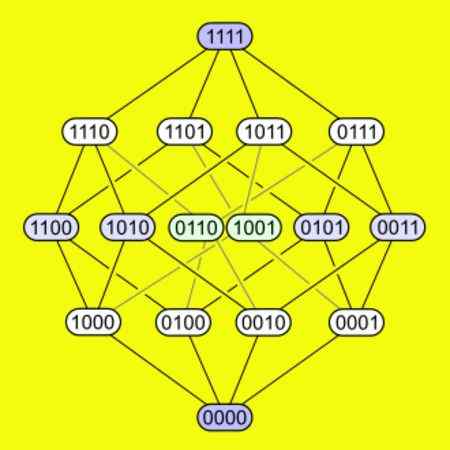Figura 5. Os 16 vértices de um hipercubo quatro dimensional são mostrados e como eles se conectam a mesma. Fonte: Wikimedia Commons.

Desdobrado de um hipercubo

Uma figura geométrica regular, por exemplo, um poliedro, pode ser desdobrado em vários números de dimensionalidade inferior.

No caso de um 2 cubo (um quadrado) pode ser desdobrado em quatro segmentos, ou seja, quatro 1 cubo.

Pode servir a você: Distribuição de Poisson: fórmulas, equações, modelo, propriedades

Da mesma forma, um 3 cubo pode ser desdobrado em seis 2 cubo.

Figura 6. Um n-cubo pode ser desdobrado em vários (n-1) -Cubos. Fonte: Wikimedia Commons.

Um 4 cubo (testerato) pode ser desdobrado em oito 3 cubos.

A animação a seguir mostra o desdobramento de uma tripa.

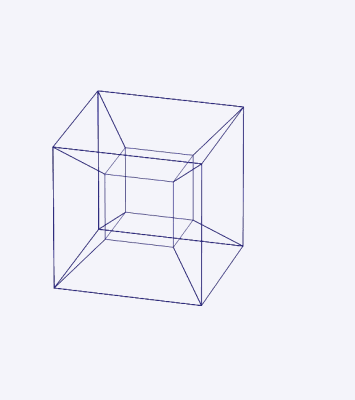Figura 7. Um hipercubo 4 -dimensional pode ser desdobrado em oito cubos tridimensionais. Fonte: Wikimedia Commons. Figura 8. Projeção tridimensional de um hipercubo quatro dimensionais fazendo uma rotação dupla em torno de dois aviões ortogonais. Fonte: Wikimedia Commons.

Referências

1. Cultura científica. Hypercubo, visualizando a quarta dimensão. Recuperado de: culturacientifica.com
2. Epsilones. Hipercubo tetradimensional ou tesserato. Recuperado de: epsilonas.com
3. Perez R, Aguilera A. Um método para obter um teste do desenvolvimento de um hipercubo (4D). Recuperado de: ResearchGate.líquido
4. Wikilibros. Matemática, Polyedra, Hipercubos. Recuperado de: é.Wikibooks.org
5. Wikipedia.  Hypercube. Recuperado de: em.Wikipedia.com
6. Wikipedia. Tesseract. Recuperado de: em.Wikipedia.com