Propriedades de Heptadecágono, diagonais, perímetro, área

Ele Heptadecágono É um polígono regular de 17 lados e 17 vértices. Sua construção pode ser feita no estilo euclidiano, ou seja, usando apenas a regra e a bússola. Foi o grande gênio da matemática Carl Friedrich Gauss (1777-1855), contando apenas 18 anos de idade, que encontrou o procedimento para sua construção em 1796. 

Aparentemente, Gauss sempre se sentiu muito inclinado a essa figura geométrica, a ponto de que, desde o dia em que descobriu sua construção, ele decidiu ser matemático. Dizem também que ele queria que o heptadecágono fosse gravado em sua lápide.

figura 1. Heptadecágono é um polígono regular de 17 lados e 17 vértices. Fonte: f. Zapata.

Gauss também encontrou a fórmula para determinar quais polígonos regulares têm a possibilidade de ser construído com regra e bússola, pois alguns não têm construção euclidiana exata.

[TOC]

Características de Heptadecágono

Quanto às suas características, como todo polígono, a soma de seus ângulos internos é importante. Em um polígono regular de n lados, a soma é dada por:

SA (n) = (n -2) *180º.

Para os heptadecágono o número de lados n é 17, O que significa que a soma de seus ângulos internos é:

SA (17) = (17 - 2) * 180º = 15 * 180º = 2700º.

Esta soma, expressa em Radianes é assim:

SA (17) = (17 - 2) * π = 15 * π = 15π

Das fórmulas anteriores, pode -se deduzir facilmente que cada ângulo interno de um heptadecágono possui uma medida α exata dada por:

α = 2700º/17 = (15/17) π radianes

Segue -se que o ângulo interno aproximadamente é:

α ≈ 158.824º

Diagonais e perímetro

Diagonal e perímetro são outros aspectos importantes. Em qualquer polígono, o número de diagonais é: 

D = n (n - 3) / 2 e no caso de Heptadecágono, como N = 17, Você tem que D = 119 diagonais.

Pode atendê -lo: trinomial

Por outro lado, se o comprimento de cada lado do heptadecágono for conhecido, então o perímetro do heptadecágon regular está simplesmente adicionando 17 vezes esse comprimento, ou o que é equivalente 17 vezes o comprimento d Em cada lado:

P = 17 D

Perímetro de heptadecágono 

Às vezes, apenas o rádio é conhecido r do heptadecágono, por isso é necessário desenvolver uma fórmula para este caso.

Para esse fim, o conceito de apótema. O apoteme é o segmento que vai do centro do polígono comum até o ponto médio de um lado. O apothem em relação ao lado é perpendicular a esse lado (veja a Figura 2).

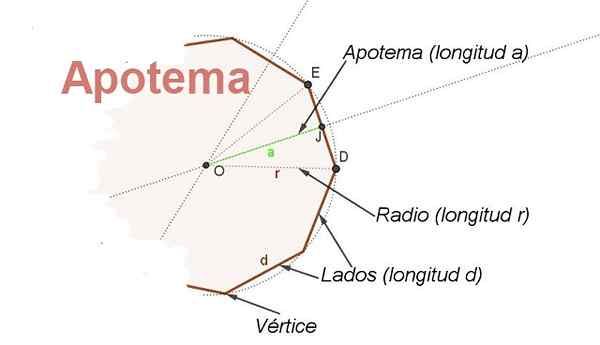Figura 2. As partes de um polígono de rádio regular e seu apothem são mostradas. (Elaboração própria)

Além disso, o apotem é bissetor do ângulo com vértice central e lados em dois vértices consecutivos do polígono, isso permite encontrar um relacionamento entre o rádio r e o lado d.

Se for chamado β para o ângulo central Corça E levando em consideração aquele apothem OJ é bissetor que você tem Ex = d/2 = r sen (β/2), onde você tem um relacionamento para encontrar o comprimento d ao lado de um polígono conhecia seu rádio r e seu ângulo central β:

D = 2 r sin (β/2)

No caso de Heptadecágon β = 360º/17 Para o que você tem:

D = 2 r sen (180º/17) ≈ 0,3675 r

Finalmente, a fórmula do perímetro do heptadecágono sabe que seu raio é obtido:

P = 34 r sen (180º/17) ≈ 6.2475 r

O perímetro de um heptadecágonon Pcir = 2π r ≈ 6.2832 r.

Área

Para determinar a área de Heptadecágono, nos referiremos à Figura 2, que mostra os lados e o apotem de um polígono regular de n lados. Nessa figura o triângulo EOD Tem uma área igual à base d (lado do polígono) por altura para (Polygon Apothem) dividido por 2:

Pode servir a você: série de poder: exemplos e exercícios

EOD = (D X A) / 2

Então, aquele apoteme conhecido para do heptadecágono e o lado d do mesmo é:

Área de Heptadecágono = (17/2) (D x A)

Área dada o lado

Para obter uma fórmula para a área de Heptadecágono, conhecendo a duração de seus dezessete lados, é necessário alcançar uma relação entre o comprimento do apoteme para e o lado d.

Em referência à Figura 2, você tem o seguinte relacionamento trigonométrico:

Tan (β/ 2) = por exemplo/ oj = (d/ 2)/ a, ser β para o ângulo central Corça. Para que o apothem para pode ser calculado se o comprimento for conhecido d Do lado do polígono e do ângulo central β:

A = (d/2) cotan (β/2)

Se essa expressão para apotem for substituída agora, na fórmula da área de Heptadecágono obtida na seção anterior, você tem:

Área de Heptadecágono = (17/4) (D²) Cotan (β/2)

Ser β = 360º/17 Para o heptadecágono, então você finalmente tem a fórmula desejada:

Área de Heptadecágono = (17/4) (D²) Cotan (180º/17)

Área dada o rádio

Nas seções anteriores, foi encontrada uma relação entre o lado D de um polígono regular e sua Radio R R, sendo o seguinte: o seguinte: o seguinte é:

D = 2 r sin (β/2)

Esta expressão para d É introduzido na expressão obtida na seção anterior para a área. Se as substituições e simplificações relevantes forem feitas, é obtida a fórmula que permite calcular a área de heptadecágono:

Área de Heptadecágono = (17/2) (R²) Sin (β) = (17/2) (r²) Sen (360º/17)

Uma expressão aproximada para a área é:

Área de Heptadecágono = 3.0706 (R²) 

Como esperado, esta área é um pouco menor que a área do círculo que circunscreve para o heptadecágon PARA_Circ = π r² ≈ 3.1416 r². Para ser preciso, é 2% menor que o de seu círculo circunscrito.

Pode servir a você: área de um pentágono regular e irregular: como é tomado, exercícios

Exemplos

Exemplo 1

Para que um heptadecágono tenha 2 cm de lados, que valor deve o raio e o diâmetro da circunferência circunscrita ter? Encontre também o valor do perímetro.

Para responder à pergunta, é necessário lembrar a relação entre o lado e o raio de um polígono regular de N lados:

 D = 2 r sen (180º / n)

Para Heptadecágono N = 17, pelo que D = 0,3675 r, Em outras palavras

10.8844 cm de diâmetro.

O perímetro de um heptadecágon lateral de 2 cm é p = 17* 2 cm = 34 cm.

Exemplo 2

Quanto é a área de um lado regular de heptadecágono de 2 cm?

É necessário se referir à fórmula demonstrada na seção anterior, que permite encontrar a área de um heptadecágono quando o comprimento é d Do seu lado:

Área de Heptadecágono = (17/4) (D²) / Tan (180º / 17) 

Ao substituir D = 2 cm na fórmula anterior são obtidos:

Área = 90,94 cm

Referências

1. C. E. PARA. (2003). Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
2. Campos, f., CERECEDO, f. J. (2014). Matemática 2. Grupo editorial da Patria.
3. Libertado, k. (2007). Descubra polígonos. Companhia de Educação de Benchmark.
4. Hendrik, v. (2013). Polígonos generalizados. Birkhäuser.
5. Iger. (s.F.). Matemática Primeiro Semestre Tacaná. Iger.
6. Jr. Geometria. (2014). Polígonos. Lulu Press, Inc.
7. Miller, Heeren e Hornsby. (2006). Matemática: Raciocínio e Aplicações (Décima Edição). Pearson Education.
8. Patiño, m. (2006). Matemática 5. Editorial Progreso.
9. Sada, m. 17 lados regulares com regra e bússola. Recuperado de: Geogebra.org
10. Wikipedia. Heptadecágono. Recuperado de: é.Wikipedia.com