Grau de um polinômio como é determinado, exemplos e exercícios

Ele grau de um polinômio em a A variável é dada pelo termo que o principal expoente tem e se o polinomial tem Duas ou mais variáveis, Então o grau é determinado pela soma dos expoentes de cada termo, a soma principal do ser polinomial.

Vamos ver como determinar o grau de polinomial de uma maneira prática.

figura 1. A famosa equação de Einstein para energia E é um monômio absoluto de grau 1 para a variável de massa, indicada por m, uma vez que a velocidade da luz C é considerada constante. Fonte: piqsels.

Suponha que o polinomial p (x) = -5x + 8x³ + 7 - 4x². Este polinômio é de uma variável, neste caso é a variável x. Este polinomial consiste em vários termos, que são os seguintes:

-5x; 8x³; 7; - 4x²

 Vamos selecionar entre os quatro termos cujo expoente é maior, este termo é:

8x³

E agora qual é o expoente? A resposta é 3. Portanto, p (x) é um polinômio de grau 3.

Se o polinômio em questão tiver mais de uma variável, o grau pode ser:

-Absoluto

-Em relação a uma variável

O grau absoluto é explicado no início: adicionando os expoentes de cada termo e selecionando o maior.

Por outro lado, o grau de polinômio em relação a uma das variáveis ​​ou letras é o maior valor do expoente que disse a carta. O ponto ficará mais claro com os exemplos e exercícios resolvidos nas seções a seguir.

[TOC]

Exemplos de grau de polinômio

Os polinômios podem ser classificados no grau, sendo capaz de ser de primeiro grau, segunda série, terceira série e assim por diante. Para o exemplo da Figura 1, a energia é um monômio de primeiro grau para a massa.

Pode servir a você: congruência: figuras congruentes, critérios, exemplos, exercícios

Também é importante observar que o número de termos que um polinômio tem é igual ao grau mais 1. Então:

-Polinômios de primeiro grau têm 2 termos: um₁x + a_qualquer

-O segundo polinômio de grau tem 3 termos: a₂x² + para₁x + a_qualquer

-Um polinômio de terceiro grau tem 4 termos: um₃x³ + para₂x² + para₁x + a_qualquer

E assim por diante. O leitor atencioso terá observado que os polinômios dos exemplos anteriores são escritos de uma maneira decrescente, ou seja, colocando primeiro o termo com o grau principal.

Vários polinômios aparecem na tabela a seguir, tanto de uma quanto de várias variáveis ​​e de seus respectivos graus absolutos:

tabela 1. Exemplos de polinômios e seus graus

Polinomial	Grau
3x4+5x3-2x+3	4
7x3-2x2+3x-6	3
6	0
X-1	1
x5-bx4+ABX3+Ab3x2	6
3x3e5 + 5x2e4 - 7xy2 + 6	8

Os dois últimos polinômios têm mais de uma variável. O termo que tem o maior grau absoluto se destacou em negrito, para que o leitor verifique rapidamente o grau. Importante lembrar que quando a variável não tem expoente por escrito, entende -se que o referido expoente é igual a 1.

Por exemplo, no termo proeminente Ab³x² Existem três variáveis, a saber: para, b e x. Nesse termo, para É elevado a 1, ou seja:

a = a¹

Portanto Ab³x² = a¹b³x²

Como o expoente de B é 3 e o de x é 2, é imediatamente seguido que o grau deste termo é:

1+3+2 = 6

E é o grau absoluto de polinômio, uma vez que nenhum outro dos termos tem um grau maior.

Procedimento para trabalhar com polinômios

Ao trabalhar com polinômios, é importante prestar atenção ao grau do mesmo, pois em primeiro lugar e antes de executar qualquer operação, é conveniente seguir estas etapas, nas quais o grau fornece informações muito importantes:

-Ordene a preferência polinômio em um sentido decrescente. Dessa forma, o termo com a nota mais alta está à esquerda e o mais baixo para o direito.

Pode atendê -lo: Endecagon

-Reduza termos semelhantes, um procedimento que consiste em adicionar todos os termos de igual variável e grau que estão na expressão algebraicamente.

-Se necessário, os polinômios são concluídos, termos intercalados cujo coeficiente é 0, em caso de termos com algum expoente.

Encomendar, reduzir e completar um polinômio

Dado o polinomial p (x) = 6x² - 5x⁴- 2x+3x+7+2x⁵  - 3x³ + x⁷ -12 É solicitado que ele diminua, reduza os termos semelhantes, se houver e completar os termos que estão faltando por serem precisos.

A primeira coisa a procurar é o termo com o grande expoente, que é o grau de polinomial, que acaba sendo:

x⁷

Portanto, p (x) é grau 7. Então o polinômio é ordenado, começando com este termo à esquerda:

P (x) = x⁷ + 2x⁵ - 5x⁴ - 3x³ + 6x² - 2x+3x+7 -12

Os termos semelhantes agora são reduzidos, que são os seguintes: - 2x e 3x, por um lado. E 7 e -12 no outro. Para reduzi -los, os coeficientes são adicionados algebricamente e a variável é deixada inalterada (se a variável não aparecer ao lado do coeficiente, deve -se lembrar que x⁰ = 1):

-2x+3x = x

7 -12 = -5

Esses resultados são substituídos em p (x):

P (x) = x⁷ +2x⁵ - 5x⁴ - 3x³ + 6x² + x -5

E, finalmente, o polinômio é examinado para verificar se um expoente está ausente e, na verdade, um termo cujo expoente está 6 está ausente; portanto, é concluído com zeros como este:

P (x) = x⁷ + 0x⁶ +2x⁵ - 5x⁴ - 3x³ + 6x² + X - 5

Agora observa -se que o polinômio foi deixado com 8 termos, pois, como dito antes, o número de termos é igual ao grau + 1.

Importância do grau de um polinômio na soma e subtração

Com polinômios, operações de soma e subtração podem ser realizadas, nas quais apenas termos semelhantes são adicionados ou subtraídos, que são a mesma variável e o mesmo grau. Se não houver termos semelhantes, a soma ou subtração será deixada simplesmente indicada.

Pode atendê -lo: propriedade distributiva

Uma vez que a soma ou subtração foi feita, sendo a soma do oposto, o grau do polinomial resultante é sempre igual ou menor que o grau de adição polinomial de maior grau.

Exercícios resolvidos

- Exercício resolvido 1

Encontre a soma a seguir e determine seu grau absoluto:

para³- 8ax²  + x³ + 5 ª²X - 6ax² - x³ + 3º³ - 5 ª²x - x³ + para³+ 14ax² - x³

Solução

É um polinômio de duas variáveis, por isso é conveniente reduzir os termos semelhantes:

para³- 8ax²  + x³ + 5 ª²X - 6ax² - x³ + 3º³ - 5 ª²x - x³ + para³+ 14ax² - x³ =

= a³ + 3º³ + para³ - 8ax² - 6ax²+ 14ax² +5 ª²X - 5a²x+ x³- x³- x³- x³ =

= 5a³ - 2x³

Ambos os termos são de grau 3 em cada variável. Portanto, o grau absoluto de polinômio é 3.

- Exercício resolvido 2

Expresse como polinomial a área da seguinte figura geométrica plana (Figura 2 à esquerda). Qual é o grau resultante de polinômio?

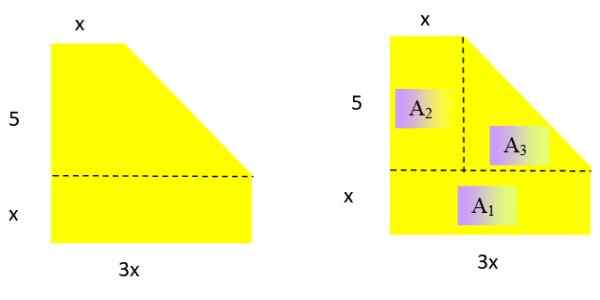Figura 2. À esquerda, a figura do ano resolveu 2 e à direita, a mesma figura decomposta em três áreas cuja expressão é conhecida. Fonte: f. Zapata.

Solução

Sendo uma área, o polinômio resultante deve ser grau 2 na variável x. Para determinar uma expressão adequada para a área, a figura é dividida em áreas conhecidas:

A área de um retângulo e um triângulo são respectivamente: Base x altura e Base x altura /2

PARA₁ = x . 3x = 3x²; PARA₂ = 5 . x = 5x; PARA₃ = 5 . (2x /2) = 5x

Observação: A base do triângulo é 3x - x = 2x e sua altura é 5.

Agora as três expressões obtidas são adicionadas, com isso você tem a área da figura, dependendo de x:

3x² + 5x + 5x = 3x² + 10x

Referências

1. Baldor, a. 1974. Álgebra Elementar. Cultural venezuelana s.PARA.
2. Jiménez, r. 2008. Álgebra. Prentice Hall.
3. Wikilibros. Polinômios. Recuperado de: é. Wikibooks.org.
4. Wikipedia. Grade (Polinomial). Recuperado de: é.Wikipedia.org.
5. Zill, d. 1984. Álgebra e trigonometria. Mac Graw Hill.