Geometria euclidiana

Explicamos o que geometria euclidiana, sua história, elementos e damos vários exemplos é

Euclides de Alexandria e seus elementos, de JUsepe de Ribera, ao lado, duas linhas não paralelas e uma linha que os corta, ilustrando o quinto postulado. Fonte: Wikimedia Commons.

O que é geometria euclidiana?

O Geometria euclidiana É o que é governado por esses postulados por Euclid de Alejandría, um geômetro grego que viveu em direção a 300 para.C, em cuja honra essa disciplina é nomeada, pois foi a primeira a sistematizar.

Este ramo da matemática estuda as propriedades de linhas, planos, ângulos e figuras geométricas, como polígonos, circunferências e outros conflitos. Daí sua importância na ciência e em engenharia, cujo desenvolvimento provocou significativamente.

Por outro lado, a geometria euclidiana foi a primeira ciência exata, já que, com ela, começou o caminho da sistematização da ciência, bem como o uso da lógica para demonstrar, a partir de alguns axiomas, numerosas proposições chamadas teoremas, a fim de descrever as propriedades de objetos geométricos.

História

A geometria tem uma longa história, porque o interesse da humanidade é muito antigo e o eixo central da geometria euclidiana é o trabalho Unid, do sábio Euclid de Alexandria, uma cidade localizada no Egito, e que viveu no século IV para.C.

Na época, as propriedades mais importantes de inúmeras figuras e corpos geométricos eram conhecidos. Havia um amplo conhecimento sobre geometria, mas tudo era empírico e carecia de sistematização.

Então, o rei do Egito Ptolomeu e confiou o já famoso professor de Euclides, cuja escola estava em Alexandria, para organizar todo o conhecimento matemático e geométrico disponível até agora, incluindo teoremas e propriedades.

Euclides começou a trabalhar e ao lado de seus discípulos, escreveu seus elementos de trabalho, que ele dividiu em treze livros, como capítulos. Este trabalho se tornaria uma referência para a geometria para as gerações futuras.

Pode atendê -lo: derivados sucessivos

Elementos de Euclides

O conteúdo dos elementos está organizado da seguinte forma:

• Nos livros I a IV geometria plana desenvolve.
• Nos livros V e eu vimos a teoria da proporção.
• IX Livros são dedicados à aritmética.
• O inesuribilidade aparece no livro x,
• A geometria do espaço nos livros xi a xiii.

A geometria euclidiana foi a base para muitos desenvolvimentos geométricos posteriores e atualmente está sendo ensinada em todas as escolas do mundo.

Ele também tem a virtude de ser o primeiro trabalho a incluir demonstrações cuidadosas com base no raciocínio lógico e também em dar coerência ao corpo de conhecimento geométrico e matemático da época.

Elementos básicos da geometria euclidiana

A geometria euclidiana é construída em torno de quatro elementos básicos, descritos no livro I dos elementos:

1. Ver
2. Direto
3. Plano
4. Espaço

1. Ver

A ver Falta dimensões ou partes e se distingue de outro ponto simplesmente por sua localização. Se dois pontos A e B são diferentes, é porque eles têm posições diferentes, que são indicadas através das coordenadas cartesianas bem conhecidas (x, y) se o ponto estiver no plano ou nas coordenadas (x, y, z) Se estiver no espaço.

Vale ressaltar que o sistema cartesiano não faz parte do Unid de Euclides, mas apareceu muito mais tarde nos 1600 anos e deve -se a René Descartes.

2. Direto

O direto É uma coleção infinita de pontos e só tem comprimento, não largura. Uma parte disso geralmente é desenhada, com setas apontando que a linha continua indefinidamente.

3. Plano

A plano É uma superfície ilimitada, por isso possui duas dimensões e das quais uma porção é representada, por meio de um quadrado ou um retângulo.

Lá, no avião, existem muitas figuras geométricas, como linhas, curvas abertas e fechadas e polígonos, entre outros.

Pode atendê -lo: equação geral de uma linha cuja inclinação é igual a 2/3

4. Espaço

Finalmente, existe o espaço Com suas três dimensões, capaz de abrigar todos os pontos. Ele contém os planos e os corpos geométricos caracterizados por seu volume, como poliedros, esferas e mais.

Estes podem ser considerados as definições básicas de geometria euclidiana, mas além dessas, Euclides oferece cerca de 150 definições variadas em seu trabalho.

Noções comuns

Eles consistem em fatos óbvios e intuitivos, que não pertencem corretamente ao escopo da geometria e são usados ​​à medida que os conceitos se desenvolvem. Eles se referem a "coisas" em um contexto muito amplo:

1. Coisas o mesmo para outra coisa, elas são iguais.
2. Se as coisas são adicionadas a outro conjunto de coisas, e todas elas são iguais, quais resultados também são iguais.
3. Se coisas iguais forem roubadas, o restante também é o mesmo.
4. Quando as coisas coincidem entre si, é porque elas são iguais.
5. O todo é sempre maior que as partes, tiradas separadamente.

Postulados de geometria euclidiana

Postulados ou axiomas são declarações simples que são consideradas verdadeiras e óbvias, para que não requerem demonstração.

Eles constituem a base da geometria euclidiana e euclida estabelece cinco em seu livro I:

1. Seja dois pontos diferentes de e B, há apenas uma linha que passa por eles, ou seja, dois pontos determinam uma linha.
2. Qualquer segmento retilíneo pode ser estendido indefinidamente para constituir uma linha, portanto, todo segmento pertence a uma linha.
3. Se você tiver dois pontos diferentes ou e A, sempre poderá desenhar um círculo com o centro em O e o raio igual ao segmento OA.
4. Todos os ângulos retos são congruentes um com o outro.
5. Dada uma linha e um ponto P que não pertence a ela, é sempre possível.

O último postulado, especialmente em sua versão original, não parece tão simples quanto os outros. Afirma que:

Pode servir você: heptagon

“Se uma linha reta que cai em duas outras linhas, faz com que os dois ângulos internos do mesmo lado menos de dois ângulos retos, disseram linhas retas, generalizadas indefinidamente, elas são (se cruzam) no lado em que os ângulos menores são que o dois ângulos retos ".

Isto é, originalmente postulado 5 estabelece a condição para que duas linhas não sejam paralelas. Mas é mais claro quando é escrito de tal maneira que ilustra o oposto, ou seja, o paralelismo das linhas.

Exemplos de geometria euclidiana

Exemplo 1

Existem três pontos diferentes, rotulados com letras A, B e C.

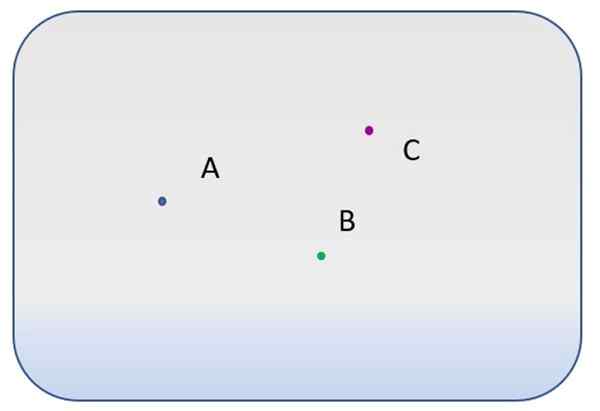
1. Quantas linhas diferentes passam pelo ponto A?
2. E quantos podem ser desenhados entre os pontos A e B? E entre A e C?
3. É possível desenhar uma linha para a qual os pontos A, B e C?

Responda para

De acordo com o Postulado I, linhas retas infinitas podem ser desenhadas através de A, uma vez que dois pontos são necessários para determinar uma linha.

Resposta b

Entre A e B só podem ser desenhados uma linha. E entre A e C também.

Resposta c

Não é possível que uma linha contenha A, B e C ao mesmo tempo.

Exemplo 2

É solicitado que construa passo a passo um triângulo equilátero (todos os seus lados são iguais), conhecendo um de seus lados, que é o segmento AB e indicando em cada etapa o postulado ou a noção comum usada na construção na construção do.

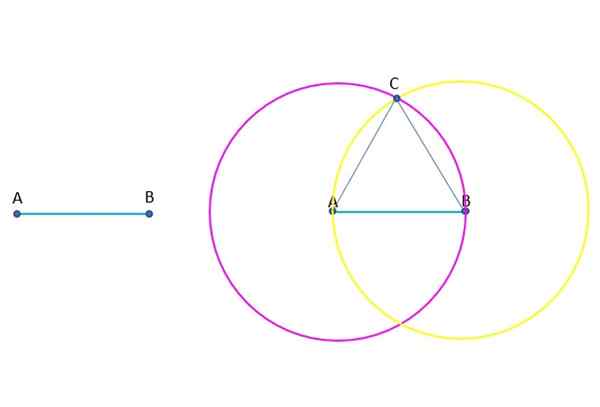Construção do Triângulo Equilateral ABC. Fonte: f. Zapata.

Responder

Passo 1

Um círculo com um centro em A e Radio AB é desenhado. Isso é sempre possível, de acordo com o postulado III.

Passo 2

Outra circunferência com o centro B e Radio AB é desenhada, e o postulado III é aplicado novamente.

etapa 3

Ambas as circunferências, que têm o mesmo raio, são cortadas no ponto C. Agora você pode desenhar segmentos que se unem C com A e B, respectivamente, de acordo com o Postulado I.

Esses segmentos são rádios da circunferência e, portanto, as medidas de CA e BC são iguais às de AB, de acordo com a noção comum 1. Então o triângulo ABC é equilateral.