Geometria analítica

Explicamos qual geometria analítica, sua história, quais estudos e aplicações são

O que é geometria analítica?

O geometria analítica É o ramo da matemática em que a geometria e a álgebra são combinadas, para resolver vários problemas geométricos através de técnicas algébricas.

Use sistemas de coordenadas, como o sistema de coordenadas cartesianas, que deve seu nome René Descartes. Dessa maneira, é possível associar curvas no avião e no espaço, com equações algébricas.

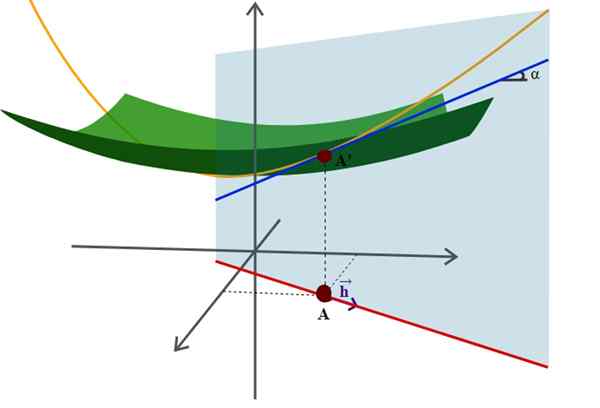
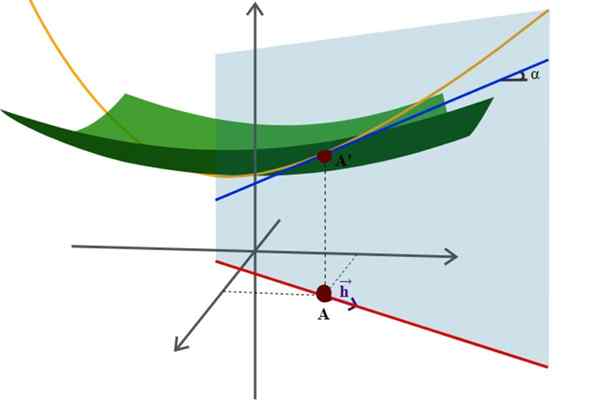Diagrama de uma superfície no espaço e seu derivado direcional, uma das muitas aplicações mais avançadas da geometria analítica. Fonte: Wikimedia Commons.

Um exemplo disso é a equação bem conhecida do raio r, centrado na origem do sistema de coordenadas:

Sem dúvida, em muitos casos, é mais simples trabalhar com a expressão algébrica de uma curva do que com sua própria representação geométrica. É o caso ao calcular interseções entre curvas ou encontrar linhas de secagem ou secagem para eles.

Da mesma forma, através da geometria analítica, é possível fazer gráficos de funções de layout. E como se sabe, as funções permitem a modelagem de problemas de ciência e engenharia. Portanto, a geometria analítica está presente nos currículos das carreiras associadas a essas áreas de conhecimento.

Breve História da Geometria Analítica

A geometria analítica tem sua origem na primeira metade do século XVII, na mão de dois matemáticos franceses notáveis: René Descartes (1596-1650) e Pierre de Fermat (1601-1665).

Rene Descartes

No entanto, pode-se dizer que seus antecedentes datam séculos, para o matemático grego Apollonius de Pergamo (262-190 A.C.). Ele escreveu um tratado sobre os cônicos, aos quais concedeu seus nomes: circunferência, elipse, parábola e hiperbola.

Pode atendê -lo: proporcionalidade composta: explicação, regra de três compostos, exercícios

Assim, o trabalho de Apollonio foi a base para, muito mais tarde, o francês René Descartes e Pierre de Fermat lançaram os fundamentos da geometria analítica, independentemente. Mas Descartes é considerado o pai desta ciência, pois ele foi o primeiro a publicar seus trabalhos.

Descartes, Fermat e Euler

No discurso do método de 1637, Descartes unificou duas disciplinas que até então haviam sido separadas: álgebra e geometria. Em seu trabalho, Descartes apresenta o sistema de coordenadas cartesianas, para localizar pontos no avião e no espaço.

Ele também utiliza equações algébricas de segundo grau com duas variáveis, para descrever as seções cônicas e se dedica a resolver problemas geométricos com eles. Também para criar uma boa parte da notação matemática que atualmente é usada.

Pierre de Fermat está mais associado à óptica do que à geometria analítica, no entanto, suas contribuições são notáveis.

Em 1629, Fermat retomou os cônicos de Apollonius de Pergamo e criou as técnicas que compõem a geometria analítica, inventando seu próprio sistema de coordenadas e definindo claramente o conceito -chave de Local geométrico, com o qual o estudo da geometria analítica começa.

No entanto, as obras de Fermat não viram a luz até 1679, publicada por seu filho, quando o matemático já havia morrido. Por esse motivo, a paternidade da geometria analítica é atribuída a Descartes.

Posteriormente, para os matemáticos franceses, o suíço Leonardo Euler (1707-1783) estabeleceu as bases formais da geometria analítica. Euler introduziu vários sistemas de coordenadas no plano e no espaço: coordenadas retangulares, polares e oblíquas, bem como transformações de um sistema para outro.

Pode atendê -lo: como as informações são obtidas em uma pesquisa?

Em seus trabalhos sobre geometria analítica, Euler também aprofundou a classificação de várias curvas, de acordo com o grau da equação algébrica representativa (terceira e quarta ordem) e estudou intensivamente suas propriedades, as equações das tangentes, as curvaturas, as simetrias e muitas mais.

Que estudos geometria analítica?

Em termos gerais, a geometria analítica se concentra no estudo de elementos geométricos, como pontos, segmentos, linhas, curvas, superfícies e volumes. Para fazer isso, como afirmado acima, estabelece equações algébricas que descrevem e relacionam esses elementos, permitindo que seu gerenciamento através de técnicas algébricas.

Os principais objetivos da geometria analítica, de uma maneira muito sumária, são os seguintes:

1. Estabeleça o sistema de coordenadas cartesianas e o sistema de coordenadas polares, para localizar pontos no plano, bem como sua extensão para pontos no espaço.
2. Desenhe segmentos, retos, curvas e superfícies no avião e espaço cartesianos.
3. Deduzir as equações que analiticamente descrevem uma curva e a construção dela no plano e/ou espaço, bem como o estudo de todas as suas propriedades.
4. Classificar curvas, superfícies e volumes.
5. Derive fórmulas fundamentais para resolver problemas em pontos notáveis, retos, planos, ângulos, paralelismo, perpendicularidade, distâncias, interseções, áreas e mais.
6. Resolver problemas geométricos mediante la aplicación de métodos algebraicos, para lo cual se deducen fórmulas referentes a puntos notables, ecuaciones para la recta, los planos, los ángulos, distancia entre puntos, entre rectas y puntos, puntos de tangencia, rectas secantes, áreas y muito mais.
7. Trabalhe com espaços vetoriais e produtos entre vetores.

Distância entre dois pontos

Como exemplo das numerosas aplicações da geometria analítica, uma das mais simples é o cálculo da distância entre dois pontos do plano. São dois pontos P₁ E P₂, de coordenadas (x₁,e₁) e (x₂,e₂) respectivamente, a distância d entre eles é calculada por:

Pode atendê -lo: trinomial

Coordenadas polares

Um ponto plano pode ser especificado através de sua distância “R” até a origem do sistema de coordenadas, chamado polo, e o ângulo que forma a linha que contém ao ponto e ao polo, com o eixo horizontal ou eixo polar.

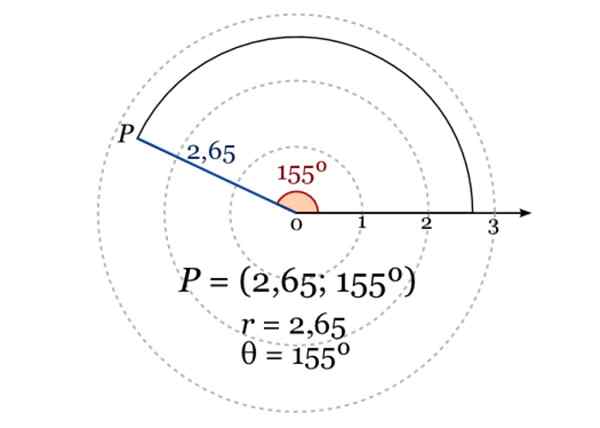A imagem mostra as coordenadas polares de um ponto P, onde r = 2.65 e o ângulo em graus em relação ao eixo polar é 155º. Fonte: Wikimedia Commons.

Aplicações de geometria analítica

Fundação do cálculo infinitesimal

A geometria analítica é essencial para o desenvolvimento do cálculo infinitesimal, pois facilita a representação gráfica de curvas e funções e trabalha com elas de maneira analítica, para criar modelos que representam fenômenos da natureza.

Mapas

O sistema de coordenadas cartesianas ajuda a fazer mapas e identificar lugares por latitude e comprimento, equivalente às coordenadas cartesianas de um ponto no plano.

Cálculos topográficos

Diferentes tipos de sistemas de coordenadas são usados ​​na topografia e constituem a base de seu estudo e aplicações. Entre eles está o sistema de coordenadas polares descrito acima.

Corpos celestes trajetórias

As seções cônicas, descritas através da geometria analítica, participam de fenômenos importantes da natureza, como as trajetórias dos corpos celestes, sujeitos à força da gravidade. Por exemplo, os planetas e alguns cometas descrevem trajetórias elípticas ao redor do sol, com isso localizado em um dos holofotes.

Arquitetura e Construção Civil

Numerosas curvas fazem parte das construções arquitetônicas, por exemplo, os cabos de uma ponte suspensa podem assumir a forma de parábolas.

Sistemas de posicionamento global

O sistema de posicionamento global ou o GPS torna possíveis locais com precisão, bem como objetos em movimento, como veículos e barcos. Também ajuda as pessoas a se tornarem mais facilmente em seus destinos, orientando -os nas melhores rotas.