Funções vetoriais

O que são funções vetoriais?

A função vetorial de um parâmetro t, É uma função cujo domínio são os valores reais de t, enquanto a rota é formada por vetores da forma r (t). Essa função pode ser expressa como:

r (t) = f (t) Yo + G (t) J + H (t) k

Onde Yo, J e k Eles são os vetores unitários nas três direções principais do espaço, e as funções f, g e h são funções reais da variável t. A notação faz uso de negrito, para distinguir magnitudes do vetor.

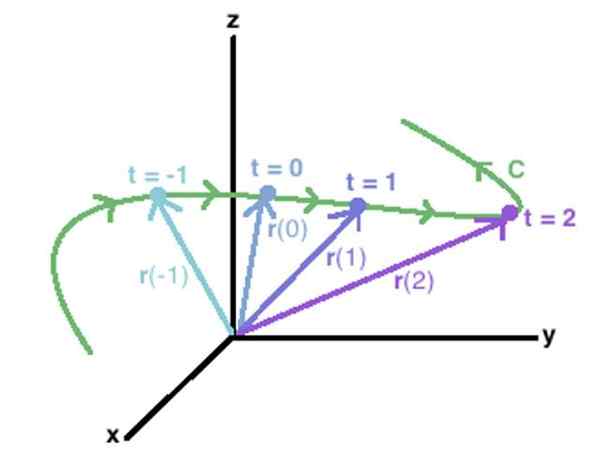Uma função vetorial no espaço pode ser usada para descrever uma curva C, juntando -se aos pontos extremos de cada um dos vetores determinados pela referida função. Fonte: Wikidot.

Outra maneira de denotar uma função vetorial é através de colchetes:

r (t) = t), G (t), H (t)>

As funções vetoriais podem ser usadas para estudar curvas no avião e no espaço, como a trajetória que segue um objeto em movimento. Um exemplo é a parábola descrita por uma bola projetada com velocidade inicial, sob gravidade.

Se você quiser saber a posição da bola a cada momento t, A função vetorial com dois componentes, uma horizontal e uma vertical:

r (t) = x (t) Yo + e(t) J

Ambos X (t) como y (t) São funções de tempo t. Assim, ao ingressar nos pontos extremos de cada um dos vetores r(t) Possível, formar a parábola descrita pela bola no avião XY.

O conceito se estende facilmente a uma curva C no espaço, como o mostrado na figura acima. Vetores aparecem nele r (-1), r (0), r (1) r (2), cujas extremidades desenham a curva C, desenhada em verde.

Limites, derivados e integrais das funções vetoriais

Ferramentas de cálculo que se aplicam a funções variáveis ​​reais também podem ser aplicadas às funções vetoriais.

Pode atendê -lo: fatorização

Limite de uma função vetorial

O limite de função vetorial r (t) = f (t) Yo + G (t) J + H (t) k, Quando t → A, é definido como:

Supondo que existam os respectivos limites de f (t), G (t) e H (t), quando t → a.

Derivado de uma função vetorial

A definição de derivado de uma função vetorial r (t) = f (t) Yo + G (t) J + H (t) k É análogo ao do derivado de uma função real de variável real. Chamando r'(t) para o referido derivado, você tem:

O derivado existe sempre que o limite anterior existe e, se assim for, a função r(t) é diferenciável em t.

Integral de uma função vetorial

Ser r (t) = f (t) Yo + G (t) J + H (t) k uma função vetorial, de modo que funções F, G e H sejam integráveis ​​em t.

Então:

Com:

C = c₁ Yo + c₂ J

O que significa que a constante de integração também é um vetor, mas constante.

Exemplos de função vetorial

Exemplo 1

Você tem a função vetorada dada por r (t) = 3SEC t Yo + 2Tan t J. É possível avaliá -lo para diferentes valores t, como t = π/4 e t = π, dando origem aos vetores r (π/4) e r (π):

r (π/4) = 3seg (π/4) Yo + 2Tan (π/4) J = 3√2 Yo + 2 J

r (π) = 3seg (π) Yo+2Tan (π) J = - 3 Yo

Porém, r (t) Ele não existe para valores de t = ∓π/2, ∓3π/2, ∓5π/2…, já que a função da SEC t = 1 /cos t Não está definido, ou é assim t = sen t / cos t.

Portanto, o domínio da função R (t) é todos os valores reais de t, exceto os da forma:

∓ (2n+1) π/2; Com n = 0, 1, 2, .. .

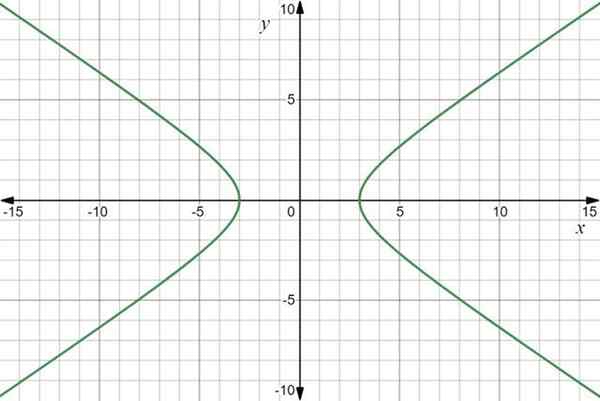
O gráfico da função é uma hipérbole:

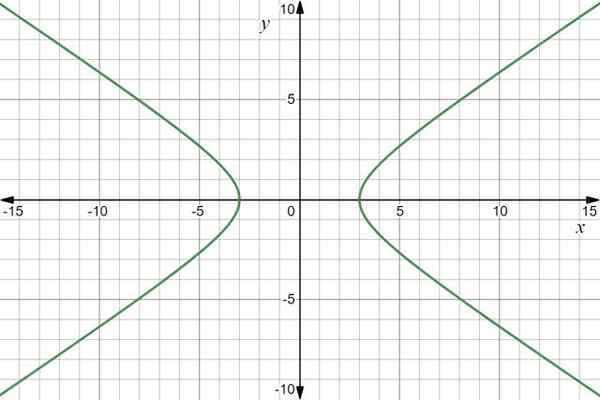Gráfico de função vetorial r (t) = 3seg t Yo+2 tan t J. Fonte: f. Zapata através de desmos.

Exemplo 2

No lançamento inclinado do projétil, a posição móvel é a função vetorial r (t) = x (t) Yo + e(t) J . Supondo que a resistência do ar não interve e que a gravidade seja a única força que age no celular, o movimento horizontal é uniforme retilíneo, enquanto a vertical é acelerada uniformemente, sendo g = 9.8 m/s² O valor de aceleração. Esta aceleração é vertical em direção ao solo.

Pode atendê -lo: regras de derivação (com exemplos)

Nesse caso, as funções x (t) e (t) Eles são, respectivamente:

• x (t) = x_qualquer + v_boi∙ t
• e (t) = y_qualquer + v_Oy∙ T - ½ gt²

Os valores v_boi e V_Oy Eles são os componentes da função vetorial que descreve a velocidade móvel o tempo todo:

v (t) = v_x(t) Yo + v_e(t) J

Com:

• v_boi = v_qualquer∙ cos θ
• v_Oy = v_qualquer∙ sen θ

Sendo θ o ângulo que forma a velocidade inicial em relação à horizontal.

Por sua parte, a posição inicial do celular é o ponto de coordenada (x_qualquer,e_qualquer), ou equivalentemente, o vetor de posição dado por:

r_qualquer (t) = x_qualquer Yo + e_qualquer J

Observe que, nas equações mostradas, o sinal negativo foi atribuído à direção vertical; portanto, o terceiro termo da equação para y (t) o leva. Também é possível atribuir a origem à posição inicial do celular.

Velocidade instantânea de projétil

A velocidade instantânea V (t) é a primeira derivada da posição, com relação ao tempo. É calculado aplicando as regras de derivação conhecidas:

v(t) = R ' (t) = [x (t) Yo + e(t) J]'= x '(t) Yo + e'(t) J = v_boi Yo + (v_Oy - Gt) J

O módulo de velocidade é dado por:

Aceleração instantânea do projétil

Sabe -se que é G, na direção vertical e na direção. Isso é verificado sabendo que a aceleração é a primeira derivada de velocidade em relação ao tempo (ou a segunda derivada da posição em relação ao tempo, se preferir):

para(t) = V ' (t) = [V_boi Yo + (v_Oy - Gt) J] '= [V_boi Yo] '+ [(v_Oy - Gt) J] '= = - g J

Este é precisamente o resultado esperado.

Exercício resolvido

Dada a função vetorial r (t) = 3T Yo + (T - 1) J, encontrar R '(t) e r "(T).

Solução

Aplicando as regras de derivação a cada um dos componentes, você tem:

Pode atendê -lo: constante de integração: significado, cálculo e exemplos

R '(t) = = 3 Yo + J

E, como o derivado de uma constante é 0:

r "(t) = 0

Quer dizer, r "(t) é igual ao vetor nulo.

Referências

1. Figueroa, d. 2005. Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
2. Larson, r. Cálculo com geometria analítica. 2º. Edição. McGraw Hill.
3. Mathonline. Funções com valor vetorial. Recuperado de: Mathonline.Wikidot.com.
4. OPENTAX. Volume 3 de cálculo. Recuperado de: OpenStax.org.
5. Purcell, e. J. 2007. Cálculo. Pearson Education.