Funções de grau Maiores que dois (exemplos)

Um (polinomial) de grau superior a dois tem a forma geral:

f (x) = a₀ + para₁x +a₂x² +.. .para_nxⁿ

Com n = 3, 4, 5,…, um número inteiro não negativo e os coeficientes para_qualquer, para₁… para_n, que geralmente são números reais.

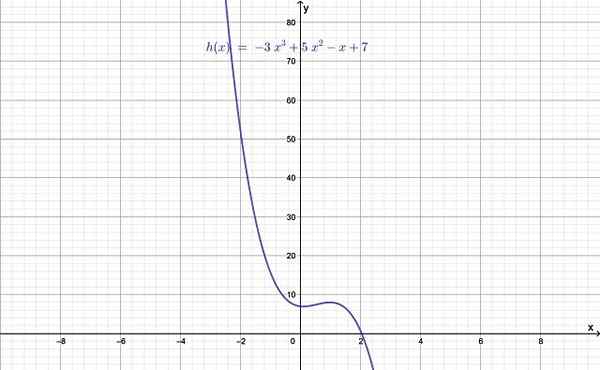figura 1.- Gráfico de uma função de grau maior que 2. Fonte: f. Zapata.

O grau da função é dado pelo valor de n, o maior dos expoentes e que por sua vez é maior que 2. Quando n = 0 é uma função constante, se n = 1 é uma função linear e, finalmente, com n = 2 é uma função quadrática.

Exemplos de funções superiores a dois, na variável "X", são os seguintes:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

A função f (x) = x³ É a mais simples de todas as funções superiores a dois e seu grau é 3. Um grau 3 também é conhecido como função cúbica. Por sua parte, G (x) é grau 4, por ser 4 o expoente máximo.

O valor de n é muito importante porque determina a forma geral do gráfico e também a quantidade máxima de raízes ou interseções que a função tem com o eixo horizontal. De fato, uma função de 3 grade tocará o eixo horizontal no máximo 3 pontos, um da 4ª série o fará no máximo em 4 pontos e assim por diante.

Quanto ao termo independente, em uma função polinomial de qualquer grau, indica a interseção da função com o eixo vertical.

Características das funções polinomiais superiores a dois

Domínio

O domínio de uma função é o conjunto de valores que permitem calcular os valores de y = f (x). Para funções polinomiais, esse conjunto é o de números N reais, ou o conjunto de números complexos, se necessário para estender o domínio.

Pode atendê -lo: limites trigonométricos: como resolvê -los, exercícios resolvidos

Significa que, dada a função polinomial f (x) = a₀ + para₁x +a₂x² +.. .para_nxⁿ, Você sempre pode substituir qualquer número real, realizar as operações indicadas e obter como resultado um valor de real y = f (x) real.

Faixa

É o conjunto formado por todos os valores adquiridos f (x), ou seja, as imagens que cada valor de x tem através da função f (x). Para funções polinomiais maiores que 2, este conjunto é o de números reais.

Raízes da função

São os valores de x para os quais é cumprido que f (x) = 0. Conforme indicado acima, o grau da função indica o número máximo de raízes que pode ter, embora nem todos sejam necessariamente reais.

Quando os coeficientes da função são números reais, as raízes reais correspondem às interseções da função com o eixo x.

Exemplo 1

As raízes racionais da função f (x) = 2x³ - 9x² + 7x + 6 pode ser encontrado no teorema a seguir:

Se a raiz de f (x) = a₀ + para₁x +a₂x² +.. .para_nxⁿ É a forma B/C, portanto os valores possíveis de B são fatores de um_qualquer e os possíveis valores de C são fatores de um_n.

Para a função do exemplo, as combinações já simplificadas são: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Agora cada um é testado através do procedimento de divisão sintética, por exemplo. Quando o resíduo da divisão é 0, o valor comprovado é uma raiz:

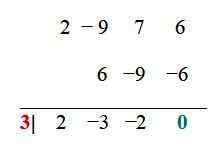
O valor x₁ = 3 é uma raiz ou zero da função, portanto (x - 3) é um fator comum de f (x), e isso pode ser escrito como:

Pode servir a você: Círculo Unitário: Funções Trigonométricas e Aplicações

f (x) = (x - 3) ∙ (2x² -3x −2)

As duas raízes restantes são os valores que satisfazem a equação 2x² −3x −2 = 0. Esta equação pode ser resolvida através da fórmula geral, uma calculadora científica ou repetindo o processo Tanteo anterior.

Essas raízes são x₂ = 2 e x₃ = - ½, e agora f (x) pode ser escrito como o produto de três fatores:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

As interseções de f (x) com o eixo x são os pontos: P₁ (3.0), P₂(2.0) e P₃(−½, 0). O gráfico da função, obtido com geogebra, mostra suas interseções com o eixo x:

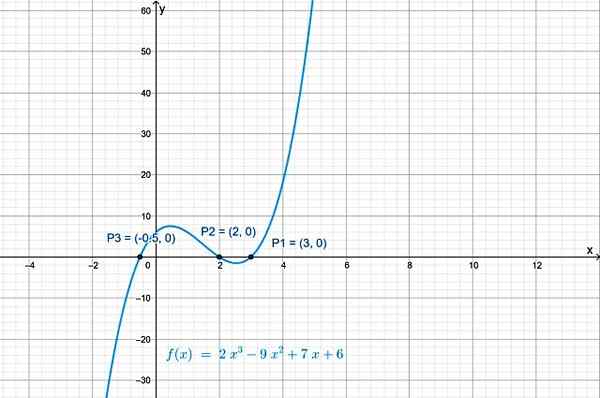Figura 2.- Uma função polinomial de grau 3 tem três cruzamentos com o eixo horizontal. Fonte: f. Zapata.

Interseção com o eixo vertical

Para encontrar a interseção da função com o eixo vertical, você deve encontrar f (0), o que é simplesmente para₀.

Exemplo 2

Encontre a interseção de f (x) = 2x³ - 9x² + 7x + 6 com o eixo vertical é muito simples, ao fazer x = 0 em f (x) é obtido:

f (x) = 6

E o ponto de interseção da função com o eixo vertical é P₄(0,6).

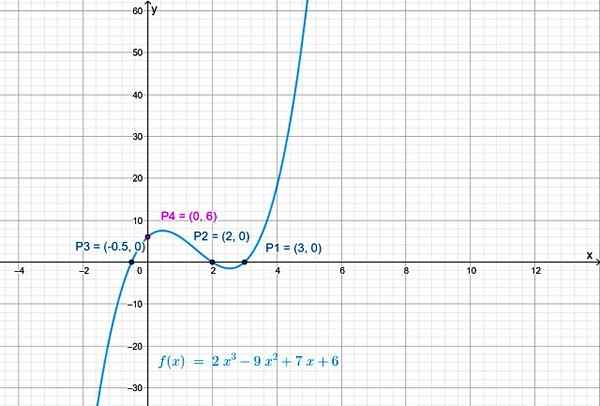Figura 3. A interseção da curva com o eixo vertical está fazendo x = 0 em f (x). Fonte: f. Zapata.

Continuidade

Funções polinômicas em geral, e em particular as de mais de 2 são funções contínuas em todo o seu domínio, isso significa que eles não têm saltos, passos, buracos ou valores para os quais não são definidos. Eles também não têm assíntotas, que são verticais, horizontais ou oblíquas diretamente às quais a função está se aproximando sem cruzá -los.

Essas qualidades de suavidade e continuidade são apreciadas nos gráficos mostrados acima.

Gráfico das funções superiores a 2

Os gráficos das funções superiores a 2 são contínuos e macios, e sua forma depende do grau do polinomial.

Pode atendê -lo: Permutações sem repetição: fórmulas, demonstração, exercícios, exemplos

Por exemplo, aqueles da grau 3 Rema tem um sinal negativo no termo com o mais alto grau).

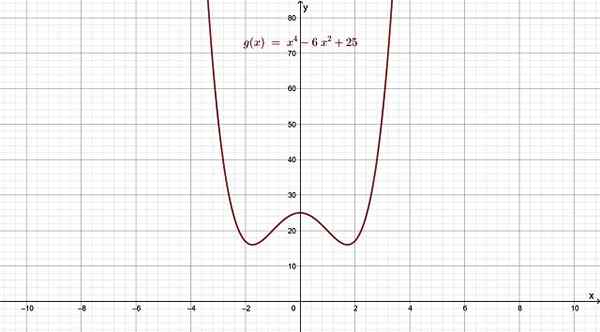Figura 4. Função poliinômica do grau 4, cujo gráfico se assemelha a uma letra w. Fonte: f. Zapata.

Para valores de x longe de x = 0, tanto para a esquerda quanto para a direita, a função se comporta como o termo de maior grau seria, porque isso prevalece sobre os outros quando X se torna muito grande ou muito pequeno.

Na imagem que segue a função f (x) = 2x é comparada³ - 9x² + 7x + 6 com a função r (x) = x³ E é apreciado que a forma de ambas as curvas seja semelhante aos valores de x que estão bem longe de x = 0.

Para valores X grandes, a função cresce rapidamente tendendo a +∞, enquanto para os valores negativos de x, a função diminui rapidamente e tende a −∞.

Figura 5.- Todas as funções de grau N se comportam da mesma forma quando se afastam de x = 0, tanto à esquerda quanto à direita. Fonte: f. Zapata.

Comparando as curvas de torque -grade (Figura 4) com o grau ímpar (Figura 2), desde que o coeficiente que acompanha o termo de grau mais alto tenha o mesmo sinal, observa -se que as curvas de grau ímpares começam de “y” negativo e crescer, enquanto os do grau -alvo começam em "y" positivo e diminuem.

Referências

1. Barnett, r. 2000. Preccultment: funções e gráficos. 4º. Edição. McGraw Hill.
2. Cálculo.DC. Funções polinômicas. Recuperado de: cálculo.DC.
3. Larson, r. 2012. Pré -cálculo. 8º. Edição. Cengage Learning.
4. Stewart, J. 2007. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
5. Tutors do time do colégio. Funções polinomiais gráficas. Recuperado de: WarsityTorm.com.