Características de função escalonadas, exemplos, exercícios

O função escalonada y = s (x) é uma função definida em peças ou peças, de modo que em um intervalo finito [a, b] tem um número finito de descontinuidades, que chamaremos de x₀ < x₁ < x₂ <… . x_n.  Em cada intervalo aberto (x_Yo , x_I+1) e tem um valor constante de valor s_Yo, Com descontinuidades -Saltos- nos pontos x_Yo.

O gráfico que resulta de uma função como essa consiste em etapas ou etapas. Vejamos um exemplo abaixo:

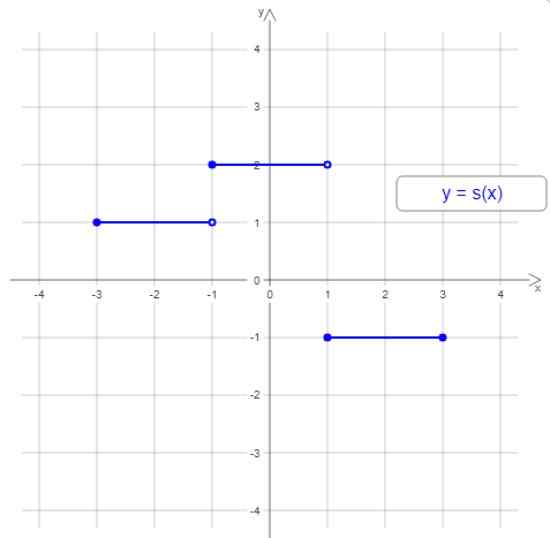
figura 1. Exemplo de função escalonada. Fonte: Wikimedia Commons.

O gráfico desta função escalonada tem três etapas ou intervalos escalonados, mas em geral a função escalonada pode ter qualquer quantidade de etapas. A largura das etapas pode ser diferente e a escada nem sempre está ascendente ou descendente.

A função escalonada do exemplo pode ser escrita especificando a largura e a alta de cada etapa, como esta:

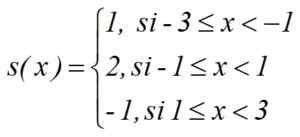
[TOC]

Características da função escalonada

-A função recebe seu nome pelo gráfico na forma de etapas, dadas pelos segmentos que o compõem. Cada segmento tem uma parte do domínio da função e em cada um, a função é constante.

-O domínio de uma função escalonada são os valores que pertencem ao intervalo para o qual é definido: [a, b], enquanto o intervalo é constituído pelos valores s_Yo das alturas dos passos.

No exemplo da Figura 1, o domínio é o intervalo [-3,3] e o intervalo é os valores -1, 1 e 2.

-A função escalonada é contínua, exceto nos valores que delimitam cada etapa, os pontos x_Yo.

-As funções Escalonada podem ser adicionadas e multiplicadas para dar origem a novas funções escalonadas.

-Sua derivada é 0 para os pontos em que é definido, pois neles a função é constante. Por sua vez, o derivado não existe em descontinuidades.

-A integral das funções escalonadas (x) entre para e b Existe e corresponde à soma das áreas dos retângulos da largura x_Yo- x_I-1 e altura s_k, igual à etapa.

Pode atendê -lo: eventos independentes: demonstração, exemplos, exercícios

Como a área de um retângulo é o produto da base por altura, temos que:

Exemplos de funções escalonadas

Dentro das funções escalonadas, existem vários tipos, por exemplo, as funções de parte inteira e a função Passo unitário, bem como várias funções escalonadas que descrevem situações comuns, como taxas de muitos serviços. Vejamos alguns exemplos:

- Exemplo 1: todas as partes inteiras

Toda a função de peça é frequentemente usando o suporte duplo:

f (x) = [[x]]

E é definido como uma função que atribui a cada número real do número inteiro mais próximo ou menor, ignorando qualquer decimal que tenha o número. Conforme o caso, temos:

Teto ou função do céu

Atribui a cada valor do domínio o número inteiro mais próximo por excesso. Por exemplo:

[[+2.56]] = 3

A parte decimal que é 0 é ignorada.56 e o ​​número inteiro mais próximo é atribuído que é maior que 2.

Outro exemplo:

[[-4.2]]= -3

Novamente a parte decimal 0 é omitida.2 e o maior número inteiro mais próximo de -4 é considerado um valor da função, que é -3.

Na figura a seguir está o gráfico da função do teto, observe que a etapa é delimitada por um pequeno círculo oco para a esquerda e um cheio para a direita, uma vez que qualquer número do intervalo, o maior número inteiro é atribuído entre as extremidades entre o termina entre as extremidades do intervalo.

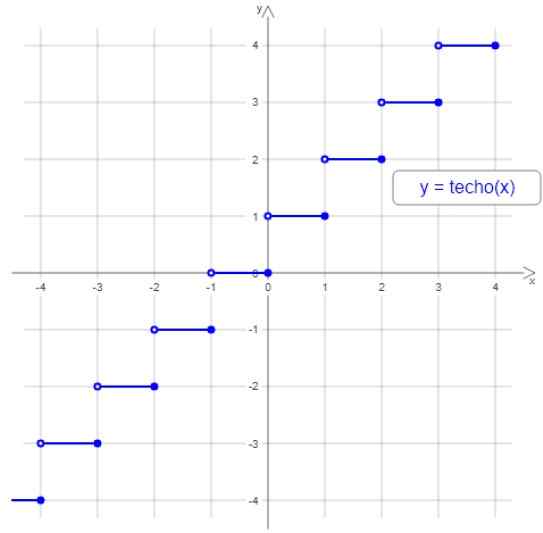Figura 2. O telhado ou a função do céu. Fonte: Wikimedia Commons.

Por exemplo, todos os valores entre 3 e 4 são atribuídos os 4 inteiros, que estão entre -2 e -1 são atribuídos o -1 e assim por diante.

Função de piso ou solo

Atribui a cada valor do domínio o número inteiro mais próximo por padrão. Exemplos desta função são:

Pode atendê -lo: quantos décimos existem em uma unidade?

[[+3.7]] = 3

[[-1.5]] = -2

[[π]] = 3

Ambas as funções são contínuas, exceto por números inteiros, onde os saltos são apresentados, e é constante para os valores entre os números inteiros K e K+1.

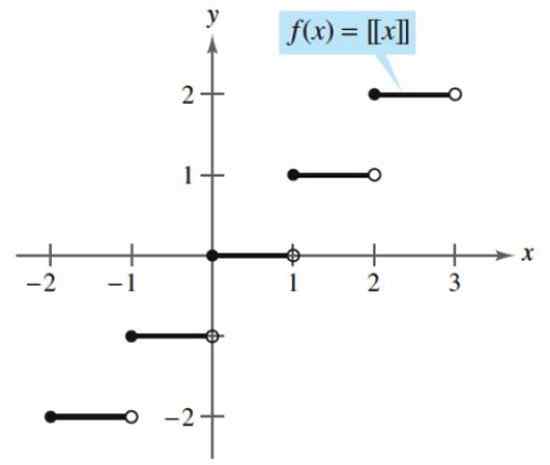Figura 3. Função de piso ou solo. Fonte: Larson, R. Cálculo de uma variável.

- Exemplo 2

Em uma cidade, a taxa de táxi é 3.US $ 65, pelos primeiros 100 m. E para cada 100 m são 0.US $ 18, sendo o limite por rota de 50 km.

É desejado estabelecer a função que relaciona a rota em medidores com o custo do serviço em $, que deve ter esse formulário:

f (x) = 3.65 + 0.18. [[x /100]] $

Onde toda a função de peça pode ser da função do céu, à qual a taxa básica que é 3 é adicionada.$ 65. Por exemplo, se quisermos saber quanto será pago por uma viagem de 6.25 km = 6250 m, teremos:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.$ 65

Se a empresa de táxis escolher uma função de piso, o cliente pagará um pouco menos pela viagem:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.$ 65

Exercícios resolvidos

- Exercício 1

Chamadas de longa distância entre as cidades A e B custam 0.40 $ 10 minutos. Após esse período, a fração ou minuto adicional vale 0.05 $.

Expressar o custo c (t) de uma chamada que dura uma certa quantidade de minutos.

Solução

Podemos expressar essa função se analisarmos o que acontece com cada opção durante a duração de uma chamada:

Para t ≤ 10 minutos

Quando t, que é o momento em que a chamada dura, é menor ou igual a 10 minutos, é paga 0.$ 40.

Pode atendê -lo: divisões de 2 dígitos resolvidas

Portanto:

f (t) = 0.US $ 40 para t incluído entre 0 e 10 minutos.

Já temos uma parte da função.

Por T> 10 minutos

Caso Entero T

Agora, vamos ver o que acontece quando o tempo de t = 10 minutos é excedido: pode acontecer que o excesso seja um número inteiro, por exemplo, que a conversa dura exatamente 11, 12, 13, 14 minutos ou mais. Nesse caso, o valor da chamada será:

f (t) = 0.40 + 0.05 (T-10) $, por t superior a 10 minutos, com T inteiro.

Ou seja, neste caso: T = 11, 12, 13, 14, 15 ... minutos.

Por exemplo, suponha que a conversa dure exatamente 15 minutos, o custo será:

f (15) = 0.40 + 0.05 (15-10) $ = 0.$ 65

Caso decimal

Por fim, considere o caso em que a chamada dura um tempo com uma parte decimal. Por exemplo, suponha que a chamada durar 15 minutos e 45 segundos, o que seria decimalmente 15.75 minutos.

Podemos expressá -lo em termos de toda a parte do tipo de piso, assumindo que a empresa deseja dar mais benefícios ao cliente ou ao céu:

f (t) = 0.40 + 0.05 ⋅ [[T-9]] $

Vamos ver o que o cliente pagaria se fosse uma função de piso:

F (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.$ 70.

Ou como uma função do céu, nesse caso o custo seria:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Função e gráfico

Como uma função definida por peças é:

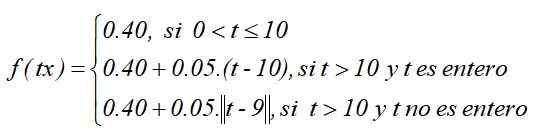
O gráfico da função seria assim, assumindo que toda a função do tipo de teto foi escolhida:

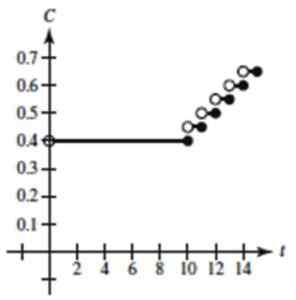Figura 4. Gráfico da função escalonada do exercício resolvido 1. Fonte: Larson, R. Cálculo de uma variável.

- Exercício 2

Calcule o integral ∫s (x) dx entre -3 e 3 da função escalonada:

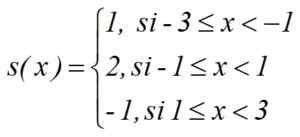
Solução

Aplicamos a definição para a integral da função escalonada:

Portanto, a integral procurada eu é:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Referências

1. Jiménez, r. 2006.Funções matemáticas. Pearson Education.
2. Larson, r. 2010. Cálculo de uma variável. 9NA. Edição. McGraw Hill.
3. Matemática IV. Funções. Recuperado de: Cobaqroo.Edu.mx.
4. Wikipedia. Funções de parte inteira. Recuperado de: é.Wikipedia.org.
5. Wikipedia. Função escalonada. Recuperado de: é.Wikipedia.org.