Função diminuindo como identificá -lo, exemplos, exercícios

A função decrescente f é aquele cujo valor diminui à medida que o valor de x aumenta. Significa que em um determinado intervalo, considerando dois valores x₁ e x₂ tais que x₁ < x₂, então f (x₁)> f (x₂).

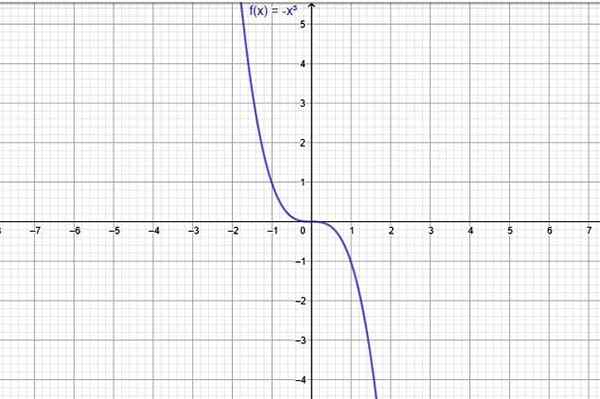
Um exemplo de uma função que está sempre diminuindo é f (x) = -x³, cujo gráfico mostra na figura a seguir:

figura 1. Uma função que sempre diminui em todo o seu domínio é f (x) = -x^3. Fonte: f. Zapata através da Geogebra.

Embora algumas funções como essa sejam caracterizadas por diminuir em todo o seu domínio, nem todos se comportam como este, há aumentando e também aqueles que crescem e diminuem em determinados intervalos de domínio. O estudo dos intervalos de crescimento e diminuição é chamado monotonia da função.

Da mesma forma, o crescimento ou diminuição da função pode ser considerado em um determinado ponto de domínio. Mas qualquer função que está diminuindo em um determinado intervalo, também é em todos os pontos que pertencem a ele.

[TOC]

Como identificar uma função decrescente?

O gráfico de função indica visualmente se está diminuindo ou não. Se, ao se mover no sentido crescente do x, a função "descendes", significa que está diminuindo.

E se você tem intervalos em que diminui e cresce alternadamente, o que é o mais comum, porque estes são claramente revelados ao observar o comportamento da função em todo o seu domínio, uma vez que haverá intervalos em que a função "ascende" e outros em que "descendo".

Como alternativa, se o gráfico de funções não estiver disponível, analiticamente é possível determinar se está diminuindo em um ponto ou em um intervalo, através da primeira derivada.

Critério da primeira derivada

Observe o comportamento da função decrescente mostrada na Figura 2. Os segmentos de linha rosa são tangentes aos pontos cujas coordenadas são [a, f (a)] e [A+h, f (a+h)] e tenha uma inclinação negativa.

Pode atendê -lo: como as informações são obtidas em uma pesquisa?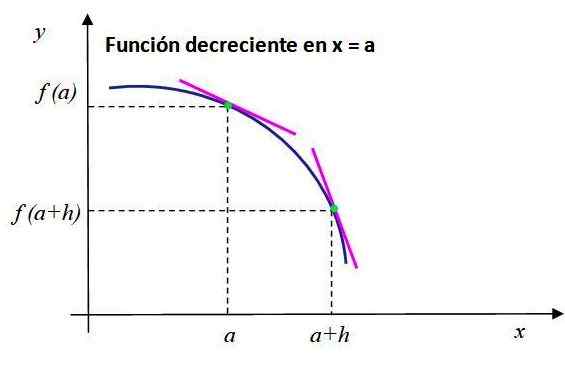Figura 2. A inclinação da linha tangente para o gráfico de f (x) é negativa em x = a, então a função está diminuindo neste ponto. Fonte: f. Zapata.

Para esta função, o seguinte é cumprido:

F (a+h) - f (a) < 0 ⇒  F (a+h) < f (a)

Portanto, pode -se pensar que a função está diminuindo em x = a.

No entanto, o primeiro derivado da função f (x), avaliado em x = a, que por definição é a inclinação da linha tangente à curva em x = a, é dada por:

O limite indica que o valor de H pode ser feito o mais pequeno que você deseja e sugere que o sinal de fa), Pode ser usado para saber se a função está ou não diminuindo em um determinado ponto, desde que o derivado exista nesse ponto.

Então sim fa) < 0, Pode -se afirmar que a função está diminuindo e pelo contrário, se f '(a)> 0, Então a função está crescendo nesse ponto.

Teorema para diminuir e crescer funções

Referência anteriormente foi feita ao comportamento da função em um ponto. Agora, o teorema a seguir permite conhecer os intervalos em que uma função está diminuindo, crescendo ou constante:

Seja f uma função diferenciável no intervalo (a, b). É verdade que:

-Sim f '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Se pelo contrário f '(x)> 0 para todos os x pertencentes a (a, b), diz -se que a função f (x) está crescendo (a, b).

-Finalmente, se f '(x) = 0 para todos os x que pertencem ao intervalo (a, b), f (x) é constante no referido intervalo.

Demonstração

Suponha que f '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ e x₂ pertencente ao referido intervalo e à condição de que x₁< x₂.

O teorema do valor médio afirma que existe um número real C, entre x₁ e x₂, tal que:

Pode atendê -lo: fator comum para agrupar termos: exemplos, exercícios

Conforme estabelecido desde x₁< x₂,  Δx é positivo. Então, como f '(c) é negativo, então Δy também é. Portanto f (x₁) é maior que f (x₂) E a função diminui efetivamente em todos os pontos do intervalo (a, b).

Etapas para saber se uma função está diminuindo

Para encontrar os intervalos de diminuição e crescimento de uma função aplicando o teorema anterior, essas etapas são seguidas:

-Encontre o primeiro derivado da função e combine -a com zero, resolvendo a equação resultante. Determine também os pontos em que o derivado não existe.

Todos esses pontos são chamados Pontos críticos E é necessário encontrá -los, pois neles o derivado tem a oportunidade de mudar seu sinal, indicativo de que a função vai do crescimento para diminuir ou pelo contrário.

-O domínio da função é dividido em intervalos determinados pelos pontos em que o primeiro derivado é cancelado ou não existe.

-Finalmente, o sinal da derivado é estudado em um ponto arbitrário que pertence a cada um dos intervalos obtidos na etapa anterior.

Exemplos de funções decrescentes

As funções nem todas diminuem na mesma taxa, algumas fazem isso mais rápido que outras. As seguintes funções, que aparecem frequentemente na prática, estão diminuindo:

A função exponencial

Uma função do formulário f (x) = a^x, Com um entre 0 e 1, sem incluir estes, diminui rapidamente em todo o domínio.

Função 1/x

Através de um programa gráfico online como geogebra, o gráfico da função f (x) = 1/x é construído, confirmando que está diminuindo em todo o seu domínio.

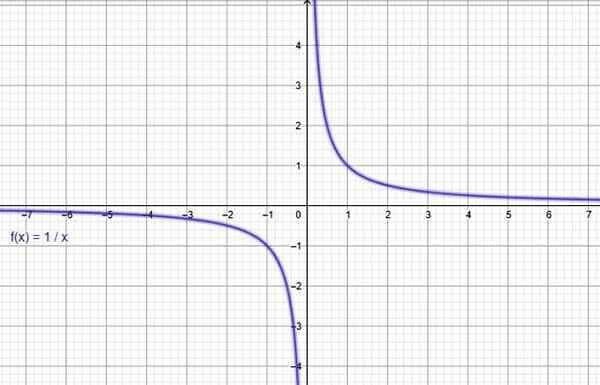Figura 3. A função f (x) = 1/x está diminuindo. Fonte: f. Zapata através da Geogebra.

A função relacionada

As funções do formulário y = mx + b com m<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Pode atendê -lo: igualdade matemática

Exercício resolvido

Encontre, se houver, os intervalos de diminuição da função:

f (x) = x⁴ - 6x² - 4

Solução

O primeiro passo é encontrar f '(x):

f '(x) = 4x³ - 12x

A primeira derivada de f (x) é uma função contínua, ou seja, não tem pontos de descontinuidade, mas é cancelada em:

4x³ - 12x = 0 = 4x (x²-3) = 0

As soluções desta equação são: x₁ = 0, x₂ = - √3 e x₃ = √3. Estes são os pontos críticos, que dividem o domínio de f (x) nos intervalos: (-∞,- √3); (- √3.0); (0, √3); (√3, ∞+).

Então o primeiro derivado em um valor x arbitrário é avaliado, que pertence a cada intervalo. Esses valores foram escolhidos:

Para (-∞,- √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32+24 = -8

Para (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4+12 = 8

Para (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

Para (√3, ∞+)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Como são vários intervalos, é uma boa idéia fazer uma mesa para organizar os resultados. A seta para cima indica que a função cresce e para baixo, o que diminui:

Conclui-se que a função diminui nos intervalos (-∞,- √3) e (0, √3) e cresce nos intervalos restantes. A função original em Geogebra é facilmente verificada pelo gráfica.

Referências

1. Ayres, f. 2000. Cálculo. 5ed. Mc Graw Hill.
2. Leithold, l. 1992. Cálculo com geometria analítica. Harla, s.PARA.
3. Purcell, e. J., Varberg, d., & Rigdon, S. E. (2007). Cálculo. México: Pearson Education.
4. Matemobile. Funções, crescendo, diminuindo e constante. Recuperado de: Matemovil.com
5. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.