Frações equivalentes a 3/4

As frações equivalentes a 3/4 São aqueles em que, dividindo o numerador entre o denominador, resulta no número decimal 0.75.

É sempre possível. Se o resultado desta operação for igual a 0.75, a fração é equivalente a 3/4, por exemplo, fração 6/8:

A fração 6/8 é equivalente a ¾, pois, dividindo o numerador entre o denominador, nos dois casos 0 é obtido.75. Fonte: f. Zapata.

Agora, a fração 6/8 foi obtida multiplicando o numerador e o denominador ¾. Ao multiplicar simultaneamente o numerador e o denominador pela mesma quantidade, o valor decimal de uma determinada fração não é alterado, mas permite obter frações equivalentes a um dado.

Outra maneira de encontrar uma fração equivalente a outra seria dividir o numerador e o denominador pela mesma quantidade. No entanto, no caso de ¾, não é possível encontrar esse número que se divide ao mesmo tempo até 3 e 4 e o resultado é inteiro. Isso ocorre porque 3 e 4 são primos entre si, então eles não têm divisores comuns.

Quando o numerador e o denominador de uma fração são números primos, diz -se que a fração é irredutível. Portanto, ¾ é irredutível.

Maneiras de encontrar uma fração equivalente a outra

Existem duas maneiras muito simples de encontrar uma fração equivalente a outra fração dada: a primeira é por redução e a segunda por amplificação.

Redução e amplificação de frações

Redução

Este procedimento consiste em encontrar um número que seja divisor do numerador e do denominador. Uma vez encontrado, o numerador e o denominador são divididos por este valor e imediatamente obtiveram uma fração equivalente ao original. É verificado que está fazendo a relação numeradora entre denominador e comparação.

Pode atendê -lo: funções matemáticas

Quando a fração irredutível de outro. A fração assim obtida é irredutível.

A fração ¾ é irredutível, como afirmado anteriormente, por ser 3 e 4 primos entre si, mas o método a seguir permite frações infinitas equivalentes a ¾.

Amplificação

Para amplificar uma determinada fração, o numerador e o denominador devem ser multiplicados pela mesma quantidade, independentemente de ser um número positivo ou negativo. Por exemplo, a fração 6/8 foi obtida pela amplificação ¾ pelo fator 2:

Embora as frações tenham um numerador e denominador diferente, ambos são os mesmos.

Observe a figura a seguir, que contém dois círculos idênticos, divididos em partes iguais, embora de tamanho diferente. Observando cuidadosamente, as áreas em verde e roxo têm a mesma medida, mas a área verde foi subdividida em 3 partes, do 4 no total que compõem o círculo da esquerda. Por outro lado, o círculo à direita foi subdividido em 8 partes iguais e a área roxa é equivalente a 6 deles.

Dessa forma, você pode representar graficamente que ¾ é equivalente a 6/8, pois ambas as frações representam a mesma quantidade.

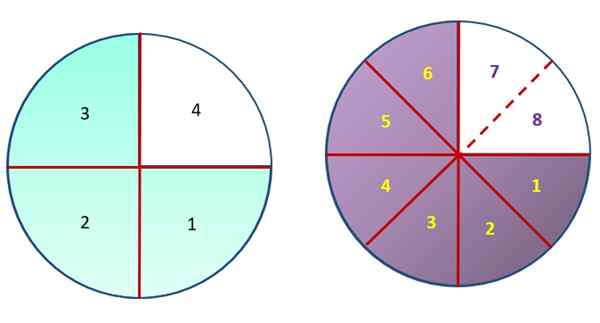As frações ¾ e 6/8 representam a mesma área nos dois círculos. Fonte: f. Zapata.

Em geral, se a fração for multiplicada ¾ pelo número n, tantas frações equivalentes a ela são obtidas como você deseja:

É importante observar que N nunca pode ser igual a 0, uma vez que a divisão por 0 não é definida. Nenhuma fração pode ter 0 no seu denominador.

Como saber se uma fração é equivalente a 3/4?

Conforme explicado no início, uma maneira de saber se uma fração é equivalente a ¾ é fazer o quociente entre o numerador e o denominador. Se for 0.75, a fração é equivalente a ¾, mas há mais alguns métodos a saber, que não exigem divisão diretamente:

Pode servir a você: mídia ponderada: como é calculado, exemplos e exercícios

Método 1

Suponha que a fração A/B, e você queira saber se é equivalente a ¾, ou seja, se é verdade que:

Para ser equivalente, o produto 4 deve ser igual ao produto 3B:

4a = 3b

Método 2

Se a fração A/B for equivalente a ¾, dividindo A e B pelo seu divisor MCD comum máximo, o resultado deve ser ¾.

Para esclarecer o uso desses métodos, consulte os seguintes exemplos.

Exemplos

Exemplo 1

Determine se a fração 150/200 é equivalente a ¾:

Pelo método 1

Nesse caso A = 150 e B = 200, deve -se cumprir que:

4a = 3b

• 4 × 150 = 600
• 3 × 200 = 600

Conclui -se que 150 /200 é equivalente a ¾.

Pelo método 2

O divisor comum máximo de 150 e 300 divide os dois exatamente. Ambas as quantidades estão em decomposição em seus principais fatores e, em seguida, fatores comuns com seu menor expoente são multiplicados:

• 150 = 2 × 5² × 3
• 200 = 2³ × 5²

Os 2 e 5 são comuns, eles multiplicam o menor poder com o qual parecem:

MCD (150, 200) = 2 × 5² = 2 × 25 = 50

Agora passamos a dividir:

Exercícios resolvidos

Exercício 1

Escreva por amplificação cinco frações equivalentes a ¾, multiplicando o numerador e o denominador a cada vez pelos seguintes números inteiros:

a) 3, b) 5, c) (-2), d) 10 e e) 20

Solução para

Solução b

Solução c

Observe que não há diferença ampliando a fração em 2 ou -2, pois, de acordo com a regra de sinais, o quociente indicado entre duas quantidades negativas é positivo.

Solução d

Solução e

Observe que esta fração é a mesma obtida pela amplificação por 2 a fração obtida acima:

Exercício 2

Verifique se as frações a seguir são equivalentes a ¾:

Pode servir a você: Coordenadas retangulares: Exemplos e exercícios resolvidos

a) 18/24; b) 21/28; c) 24/32; d) 27/38; e) 33/44

Solução para

Usando o método 1 descrito acima:

4a = 3b

Para a fração 18/24, você precisa = 18 e b = 24, então:

• 4 × 18 = 72
• 3 × 24 = 72

Portanto, 18/24 e 3/4 são equivalentes.

Solução b

De acordo com o método 2, devemos encontrar o divisor comum máximo (MCD) de 21 e 28, depois dividir ambos pelo resultado e, se a fração 3/4 for obtida, eles são equivalentes:

21 = 3 × 7
28 = 4 × 7 = 2²× 7

O fator comum é 7, portanto, MCD (21,28) = 7, então:

Solução c

Para este exercício, é verificado se o quociente entre 24 e 32 é 0 0.75:

24 ÷ 32 = 0.75

Então, 24/32 é equivalente a 3/4.

Solução d

Na fração 27/38, observa -se que 38 não é um múltiplo de 4, portanto, não é equivalente a 3/4. De qualquer forma, é realizada a proporção entre 27 e 38:

27 ÷ 38 = 0.710526

Dos quais conclui -se que 27/38 não é equivalente a 3/4.

Solução e

É fácil ver que a fração 33/44 é obtida multiplicando o numerador e o denominador de 3/4 por 11, como este:

Portanto, eles são equivalentes.