Fluxo de campo elétrico

O que é fluxo de campo elétrico?

Ele Fluxo de campo elétrico ou simplesmente fluxo elétrico é uma quantidade escalar proporcional ao número de linhas de campo elétricas que atravessam uma superfície. É denotado pelo capital da letra capital φ (phi).

O campo elétrico realmente não "flui" a maneira como um fluxo de água faz, embora as linhas de fluxo do fluido se assemelhem às do campo elétrico.

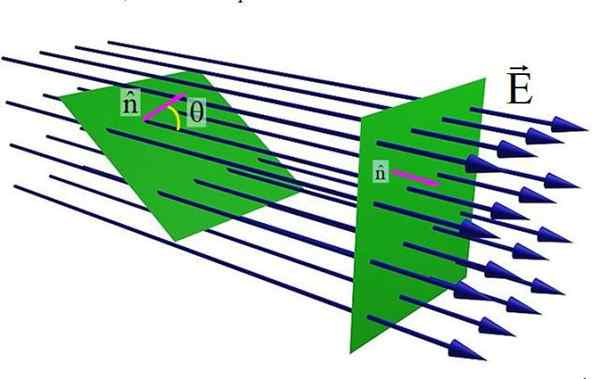
figura 1. Fluxo de campo elétrico através de uma superfície plana. Fonte: Wikimedia Commons.

A figura superior mostra uma superfície plana cruzada por um campo elétrico E. Quando o vetor de unidade normal para a superfície n e o campo E Eles são paralelos, a quantidade de linhas de campo que atravessa a superfície é máxima. Mas à medida que o ângulo θ aumenta entre n e E, O número de linhas passadas pela superfície verde é menor.

Por outro lado, o fluxo do campo elétrico também depende da magnitude de E, Porque quanto maior isso, mais linhas de campo elas cruzam a superfície. E, claro, quanto maior a área S da referida superfície, também o fluxo, então a seguinte equação é estabelecida:

Φ = e ∙ sosθ

Esta expressão é consistente com o produto escalar entre os vetores E e n:

Φ = (E • n) S

A unidade de fluxo de campo elétrico no sistema internacional de unidades se n for.m²/C (Newton X Square Metro/Coulomb). Alternativamente, como o campo também é medido em V/M (volts no metrô), o fluxo elétrico está em (v ∙ m) m).

Exemplos

De acordo com a definição, o fluxo elétrico pode ser positivo, negativo ou igual a 0. O fluxo de campo elétrico é:

Pode servir a você: Magnetização: Orbital e Moment Magnético, Exemplos

-Positivo quando o ângulo θ entre E e n É menor que 90º, pois o cos θ é maior que zero.

-Negativo se este ângulo for maior que 90º, porque então cos θ é menor que zero.

-Vazio quando θ vale exatamente 90º, porque cos 90º = 0 e as linhas de campo neste caso são tangenciais à superfície.

-Por outro lado, se o ângulo entre E e n É igual a 0, o fluxo adquire seu valor máximo.

Essas possibilidades são mostradas na seguinte imagem:

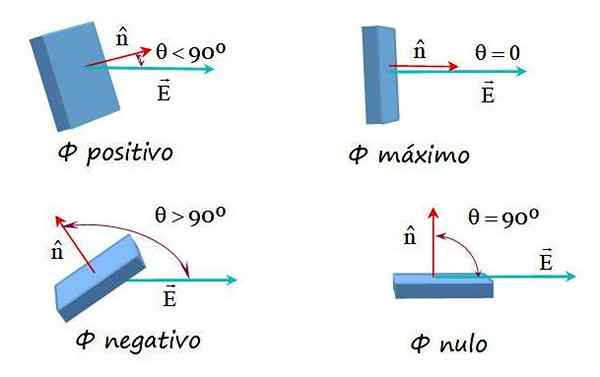Figura 2. Exemplos de fluxo de campo elétrico com várias orientações entre o campo e o vetor de superfície normal. Fonte: f. Zapata.

Fluxo de campo elétrico em uma superfície arbitrária

Anteriormente, o fluxo de campo elétrico era determinado no caso particular de um campo uniforme que afeta uma superfície plana. Para uma superfície arbitrária e/ou um campo elétrico não uniforme, o ângulo entre E e n pode variar de ponto a ponto.

Na figura seguinte, existem dois exemplos, à esquerda, uma superfície curva e à direita uma superfície fechada.

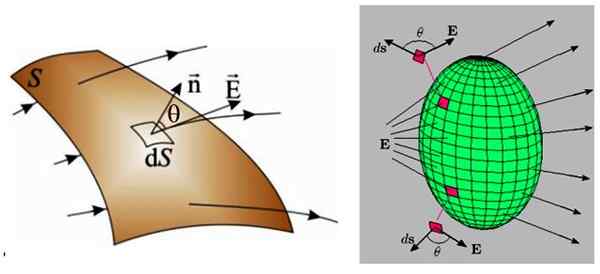Figura 3. À esquerda, uma superfície arbitrária através da qual um campo elétrico não uniforme atravessa. À direita, um campo elétrico não uniforme atravessa uma superfície fechada; portanto, o fluxo líquido nesse caso é anulado. Fonte: f. Zapata.

Em ambos os casos, a superfície é dividida em regiões muito menores, de tamanho infinitesimal, chamado DS, para o qual também atravessa um fluxo infinitesimal dφ:

dφ = (E•n) Ds = (ecosθ) ds

O campo total é obtido adicionando todas essas contribuições infinitesimais:

O símbolo de S como um subscrito na integral indica que deve ser calculado em toda a superfície. Se isso estiver fechado, é indicado com um pequeno círculo na integral:

Pode atendê -lo: Constantes Antoine: fórmulas, equações, exemplos

No caso de superfícies fechadas, n Sempre aponte, para que o fluxo tenha um sinal + quando é extrovertido, pois o ângulo entre E e n é menor que 90º e signo - quando o campo está chegando, porque então o ângulo entre E e n é maior que 90º (veja a Figura 2).

Observe que na superfície fechada à direita, o número de linhas de campo que entra na superfície é igual ao número de linhas que sai. Portanto, o fluxo líquido, definido como a soma algébrica do fluxo de entrada e o fluxo de saída, é nulo.

A fonte de campo elétrico neste caso está fora da superfície, no entanto, o fluxo líquido seria diferente de 0 se a fonte de campo elétrico (a distribuição de cargas) estivesse dentro da superfície.

Exercícios

Exercício 1

Você tem um campo elétrico E = 3.5 kN/c x e uma superfície retangular plana de 0.35 m de largura por 0.7 m de comprimento. Encontre o fluxo de campo elétrico que atravessa o retângulo nos seguintes casos:

a) A superfície é paralela ao avião yz.

b) O retângulo é paralelo ao plano XY.

c) O plano normal forma um ângulo de 40º com o eixo x e contém o eixo e.

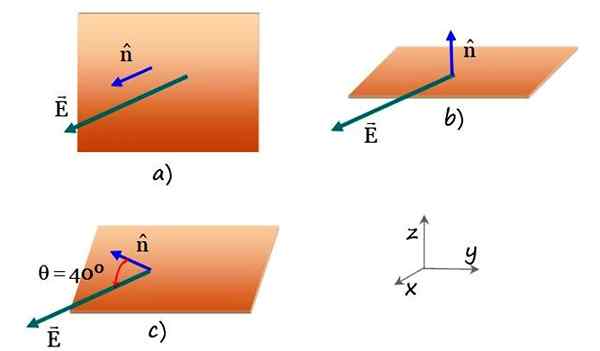Figura 4. Um plano retangular cruzado por um campo elétrico uniforme em diferentes orientações planas. Fonte: f. Zapata.

Solução para

O vetor normal e o vetor de campo elétrico são paralelos; portanto, o ângulo θ entre os dois é 0º e o fluxo elétrico é:

Φ = (e ∙ s) cos 0 = e ∙ s

A área S do retângulo é:

Pode servir a você: Método do paralelogramo: Exemplos, exercícios resolvidos

S = 0.35 m x 0.7 m = 0.245 m²

Substituindo em φ:

Φ = e ∙ s = 3.5 x 10³ N/c × 0.245 m² = 857.5 n ∙ m² /C.

Solução b

O fluxo do campo elétrico é 0, já que os vetores E e n Eles são perpendiculares um ao outro.

Solução c

O ângulo θ entre o campo E e o vetor normal n é 40º (veja a figura), portanto:

Φ = e ∙ s ∙ cos θ = 3.5 x 10³ N/c × 0.245 m² × cos 40º = 656.9 n ∙ m² /C.

Exercício 2

Calcule o fluxo de campo elétrico que produz uma carga pontual positiva que_qualquer = 2μC localizado no centro de uma esfera de raio r = 5 cm.

Solução

O campo produzido pela carga q_qualquer Não é uniforme, mas da Lei de Coulomb, sabe -se que, na superfície da esfera, ela tem uma magnitude de:

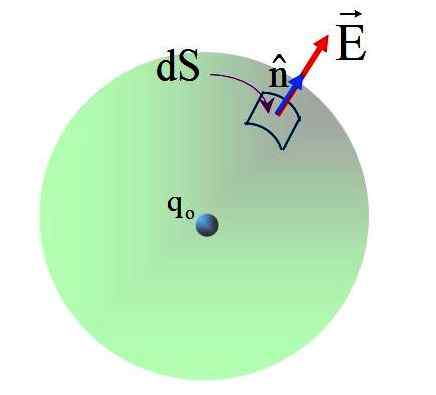Figura 5. Moscas do campo produzidas na superfície da esfera por uma carga pontual em seu centro. Fonte: f. Zapata.

O campo tem direção radial e o vetor normal n, Portanto, o ângulo entre os dois vetores é 0 em todo o ponto da superfície esférica. Substituindo:

Se tem que:

O DS de DS em toda a superfície esférica S é a área dela, que é 4πr^2, portanto:

Que conclui que o fluxo do campo elétrico não depende da superfície S, mas da carga bloqueada nele.

Seu valor é:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m²/C = 2.3 x 10⁵ N⋅m²/C

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 5. Eletrostática. Editado por Douglas Figueroa (USB).
3. Giambattista, a. 2010. Física. 2º. Ed. McGraw Hill.
4. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1. Pearson.