Fator de embalagem

O fator de embalagem é uma fração que indica quanta volume as partículas ocupam, sejam átomos, íons ou moléculas, no espaço interno de um cristal. Seu valor é sempre menor que 1, que se torna 100% do volume do vidro; Mais exatamente, sua célula unitária, que é a menor representação de todo o vidro.

Um fator de embalagem de 100% significa que as partículas ocupam o volume da célula unitária em sua totalidade. Fisicamente, é impossível que isso aconteça, porque implicaria, por exemplo, que os átomos deformem seus rádios e se dissolvessem como se fossem um "líquido eletrônico". A geometria dos átomos, esférica por conveniência, sempre resulta em espaços vazios durante a embalagem.

Como acontece em máquinas de distribuição doce, o fator de embalagem nos diz como é "apertado" as partículas de um cristal: quanto maior é, mais chiclete, ou átomos, haverá no espaço

Na definição do fator de embalagem, supõe -se que os átomos consistem em esferas rígidas, como chicletes ou bolas de doce de uma máquina dispensada (imagem superior). Entre as esferas, sempre haverá espaços ocos onde esferas menores (impurezas ou aditivos podem ser furtivos).

Se aumentarmos o fator de embalagem, as esferas serão espremidas, transformando o vidro mais compacto e denso; ou por outro lado, mais deformável, como nos metais maleáveis ​​e dúcteis.

O fator de embalagem se aplica a qualquer tipo de vidro. No entanto, seu cálculo pode se tornar um pouco tedioso, por isso será considerado apenas para cristais atômicos com estruturas simples.

[TOC]

Fórmula do fator de embalagem

O fator de embalagem é geralmente expresso como porcentagens. Por exemplo, se seu valor for 40%, significa que as partículas mal ocupam 40% do espaço total da célula unitária; ou o que é o mesmo que afirmar que 60% do vidro está "vazio".

O exposto acima esclarece qual é a fórmula para calcular esse fator:

• Ugly = (volume de átomos)/ (volume da célula unitária)

Onde significa feio Fator de empacotamento atômico, Quais são os cristais mais simples.

O volume da célula unitária depende de seus parâmetros (como o comprimento de seus lados), com o qual é procedido por uma geometria simples para calcular seu volume. Os átomos, por outro lado, são aqueles que definem a célula, por isso é possível expressar as dimensões da mesma dos rádios atômicos, como será visto nas próximas seções.

Pode servir a você: Mix racêmico: quiralidade, exemplos

No que diz respeito ao volume de átomos, o número total deles presente na célula unitária (1, 2, 3, etc.), bem como sua geometria esférica. Portanto, a fórmula é modificada um pouco:

Ugly = (nº átomos) (volume do átomo)/ (volume da célula unitária)

Para calcular feio, você deve determinar então_átomo e V_{Célula unitária}.

Simples cúbico

Célula unitária cúbica simples. Fonte: ccc_crystal_cell_ (opaco).Svg: *cobique_centre_atomes_par_maille.SVG: CDANG (IDEA ORIGINAL E EXECUÇÃO DE SVG), SAMUEL DUPRÉ (3D Odeeling with Solidworks) Derive Trabalho: Daniele Pugliesi (Talk) Derive Trabalho: Daniele Pugliesi, CC BY-SA 3.0, via Wikimedia Commons

A célula unitária mais simples de todos é o simples cúbico. Nele, temos algumas porções de átomos em cada um dos cantos. Se virmos, notaremos que o comprimento para A partir desta célula, é igual a 2R, pois são os átomos que definem a célula. Portanto, o volume da célula unitária será igual a:

V_{Célula unitária} = para³ (volume de um cubo)

= (2R)³

= 8r³

Enquanto isso, o volume do átomo será igual a:

V_átomo = (4/3) πr³ (volume de uma esfera)

Cada um dos cantos é compartilhado por outras 8 células unitárias vizinhas. Portanto, temos uma fração 1/8 em cada canto e, com 8 deles, não nos importamos com 1 átomo por unidade de célula (1/8 x 8 = 1).

O fator de embalagem é:

Feio = (1) (4/3) πr³ /8r³

= π/6 ≈ 52%

Isto é, em uma célula cúbica simples, os átomos ocupam 52% de todo o volume de vidro.

Cúbico centrado no corpo

Determinação do volume celular

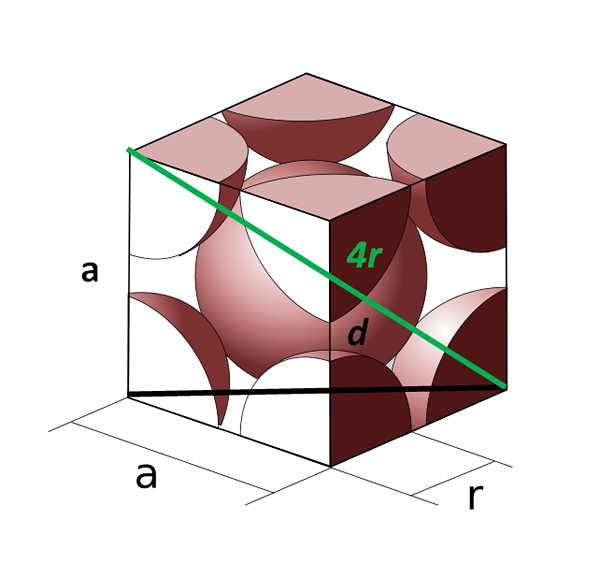Células unitárias do corpo centradas no corpo. Fonte: cobique_centre_atomes_par_maille.SVG: CDANG (IDEA ORIGINAL E EXECUÇÃO SVG), Samuel Dupré (3D Odeeling With Solidworks) Trabalho derivado: Daniele Pugliesi, CC BY-SA 3.0, via Wikimedia Commons

Agora vamos ver a célula cúbica centrada no corpo. O lado para Não pode mais ser igual a 2R, porque temos um espaço vazio entre os dois átomos dos cantos. Existe, portanto, uma diagonal d igual a 4r (cor verde) que atravessa a célula através do centro e tocam os cantos opostos, e outra diagonal d do rosto (preto).

Os lados para, d e 4r desenhe um triângulo retângulo ao qual podemos aplicar a trigonometria para calcular qual é o valor de para:

(4r)² = d² + para²

Pode atendê -lo: forças intermoleculares

Mas, por outro lado, na base da célula unitária, temos outro triângulo (para, para e d) para o qual podemos calcular a hipotenusa:

d²  = a² + para²

= 2a²

Substituindo então teremos:

(4r)² = (2º²) + a²

(4r)² = 3a²

A = (4/√3) r

O V_{Célula unitária} É igual a:

V_{Célula unitária} = a³

= ((4/√3) r)³

Determinação do fator de embalagem

Observe que, com relação ao número de átomos, temos 1 átomo dentro desta célula, seguindo a mesma dedução feita para a célula cúbica simples e outro átomo adicional localizado no centro da célula. Assim, há um total de 2 átomos para cada célula cúbica centrada no corpo.

O fator de embalagem é então:

Feio = (2) (4/3) πr³ / ((4/ √3) r)³

= (√3/8) π ≈ 68%

Isto é, em uma célula cúbica focada no corpo, 68% do volume de vidro é ocupado por átomos. Consequentemente, esse arranjo cristalino é mais compacto (ou denso) do que o simples cúbico.

Cúbico centrado em rostos

Determinação do volume celular

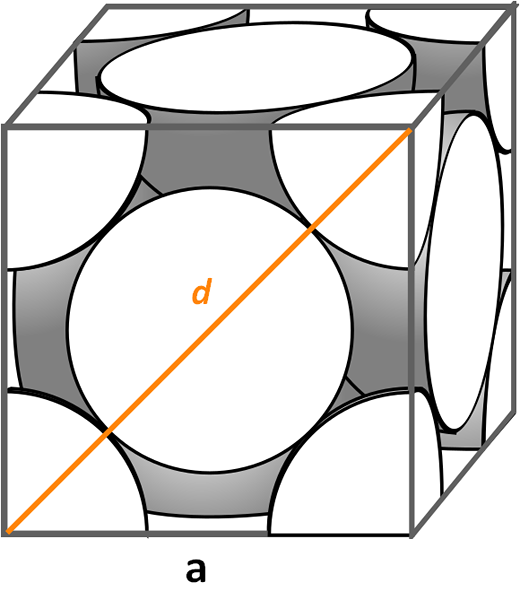Célula unitária cúbica centrada em rostos. Fonte: CDANG, CC BY-SA 3.0, via Wikimedia Commons

Vejamos a célula unitária cúbica centrada nos rostos, muito comum em sinfinas de sais inorgânicos e alguns metais, como ouro e prata. Para determinar seu fator de embalagem, devemos começar, seguindo os exemplos anteriores, para descobrir qual é o volume de sua célula unitária. É necessário calcular o lado novamente para E assim o volume do cubo para³.

Desta vez, o procedimento é mais fácil e mais direto, porque temos uma diagonal d Frente isso, junto com os lados para, Eles formam um triângulo certo ao qual podemos aplicar a trigonometria:

d² = a² + para²

= 2a²

Limpeza para nós teremos:

para = D/√2

Mas, notaremos visualmente que d É igual a 4R, por isso fazemos uma substituição:

para = 4r/√2

= 2r 2^1-1/2

= (2√2) r

Sendo v_{Célula unitária} igual a:

para³ = ((2√2) r)³

= (16√2) r³

Em relação ao número de átomos por célula, temos oito porções de um átomo em cada canto e também metade do átomo para cada uma das seis faces, que é compartilhada por outra célula vizinha. Portanto, o número de átomos é igual a:

Nº átomos = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Determinação do fator de embalagem

Tendo isso, existem 4 átomos em cada célula cúbica focada em faces e também seu volume, que é igual a (16√2) r³, Podemos então calcular o fator de embalagem:

Ugly = (nº átomos) (volume do átomo)/ (volume da célula unitária)

= (4) (4/3) πr³ / (16√2) r³

Pode atendê -lo: grupo acilo: estrutura, características, compostos e derivados

= π/(3√2) ≈ 74%

Observe que esta célula é ainda mais compacta que os anteriores: 74% do volume total da célula é ocupado por átomos. Em um cristal perfeito e puro, isso seria equivalente a dizer que 26% de seu volume está disponível para hospedar outros átomos de convidados.

Hexagonal compacto

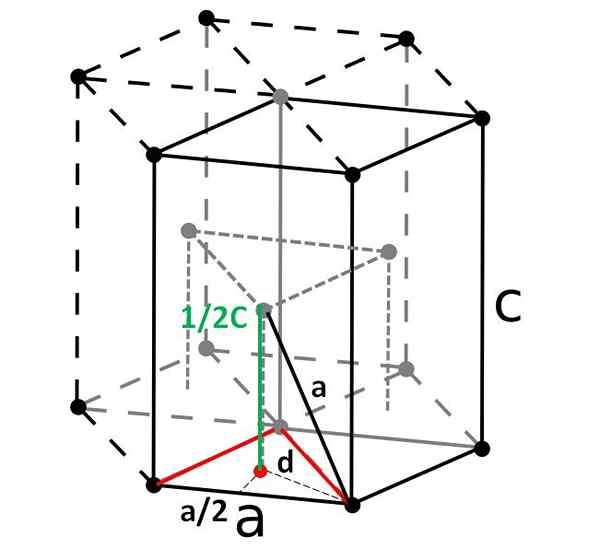Célula hexagonal compacta e sua célula primitiva romboédrica. Fonte: Original: DornEnfvector: DePiep, CC BY-SA 3.0, via Wikimedia Commons

Finalmente, entre as células unitárias mais simples e compactas, temos o compacto hexagonal. Ao contrário dos anteriores, o cálculo de seu volume é um pouco mais pesado. Como pode ser visto, não é cúbico, por isso tem dois parâmetros para e c, Este último é a altura da célula.

Determinação da altura da célula

A célula hexagonal pode ser dividida em três células de Romboyan e, de uma delas, será calculada para e c. O lado para, Embora não seja tão evidente na imagem acima, é igual a 2r. Calcular c, Em vez disso, usamos o triângulo e o produto do ponto vermelho do prisma triangular interno da mesma célula.

Precisamos calcular a distância d Ser capaz de determinar quanto vale c. No chão, o triângulo vermelho é equilátero, com um ângulo de 60º. Mas se outro triângulo retangular interno for considerado com os lados para/2 e d, e um ângulo de 30º (metade), então por trigonometria, podemos determinar d:

Cos (30º) = (para/2) / d

d = para/√3

E agora consideramos o triângulo certo composto pelos lados c/2 (verde), para (Preto e d (pontilhado):

para² = (para/√3)² + (C/2)²

Limpeza c Nós teríamos:

c = √ (8/3) para

E substituindo para Por 2R:

c = √ (8/3) (2R)

= √ (4 · 2/3) (2R)

= 4√ (2/3) r

Determinação do volume celular

Para determinar o volume da célula hexagonal, você precisa multiplicar a área hexágona por sua altura. Sabendo que triângulos equiláteis têm lados para, Sua altura é calculada h. Assim, encontrando a área de um triângulo, que é para este caso √3/4para², Multiplamos esse valor por 6 para obter a área hexagona: 3 (√3/2)para²

O volume é, portanto:

V_{Célula unitária} = Área hexágona x altura

= 3 (√3/2)para² X 4√ (2/3) r

E substituindo mais uma vez para Por 2R:

V_{Célula unitária}  = 3 (√3/2) (2r)² X 4√ (2/3) r

= 24√2 r³

Determinação do fator de embalagem

Na célula hexagonal, existem 12 átomos nos cantos, que têm 1/6 de seus volumes dentro. Existem também três átomos internos cujos volumes estão completos e outros 2 átomos nas faces superior e inferior cuja metade de seus volumes está dentro da célula.

Portanto, o número de átomos é igual a:

Nº átomo = 1/6 (12) + 1 (3) + 1/2 (2) = 6 átomos

E o fator de embalagem é finalmente:

Ugly = (nº átomos) (volume do átomo)/ (volume da célula unitária)

= (6) (4/3) πr³ / 24√2 r³

= π/(3√2) ≈ 74%

Observe que o fator de compartimento para a célula hexagonal é o mesmo que para a célula cúbica centrada nas faces. Isto é, ambos são igualmente compactos.

Referências

1. C. Barry Carter & M. Grant Norton. (2007). Ciência e Engenharia de Materiais de Cerâmica. Springer.
2. Shiver & Atkins. (2008). Química Inorgânica. (Quarta edição). Mc Graw Hill.
3. Whitten, Davis, Peck e Stanley. (2008). Química. (8ª ed.). Cengage Learning.
4. Wikipedia. (2021). Fator de empacotamento atômico. Recuperado de: em.Wikipedia.org
5. Brandon. (2021). O que é o fator de embalagem atômica (e como calculá -lo para SC, BCC, FCC e HCP)? Estudante de ciência e engenharia de materiais. Recuperado de: mSestudent.com