Fator comum para agrupar exemplos de termos, exercícios

Ele fator comum para agrupar os termos É um procedimento algébrico que permite escrever algumas expressões algébricas na forma de fatores. Para atingir esse objetivo, a expressão deve primeiro ser convenientemente agrupando e observando que cada grupo assim formado tenha, com efeito, um fator comum.

A aplicação da técnica requer corretamente alguma prática, mas em pouco tempo é possível dominar. Vamos parecer primeiro um exemplo ilustrativo descrito passo a passo. Então o leitor pode aplicar o que aprendeu em cada um dos exercícios que aparecerão depois.

figura 1. Remover fator comum para agrupamento Termos facilitam o trabalho com expressões algébricas. Fonte: Pixabay.

Por exemplo, suponha que você precise considerar a seguinte expressão:

2x² + 2xy - 3zx - 3zy

Esta expressão algébrica consiste em 4 monômios ou termos, separados por sinais + e -, a saber::

2x², 2xy, -3zx, -3zy

Observando cuidadosamente, o X é comum aos três primeiros, mas não ao último, enquanto o e é comum ao segundo e quarto, e o Z é comum ao terceiro e ao quarto.

Portanto, em princípio, não há fator comum para os quatro termos ao mesmo tempo, mas se eles forem agrupados como será exibido na seção a seguir, pode -se ajudar a escrever a expressão como o produto de dois ou mais fatores.

[TOC]

Exemplos

Fator a expressão: 2x² + 2xy - 3zx - 3zy

Passo 1: Grupo

2x² + 2xy - 3zx - 3zy = (2x² + 2xy) + (-3zx - 3zy)

Etapa 2: Remova o fator comum de cada grupo

2x² + 2xy - 3zx - 3zy =

= (2x² + 2xy) - (3zx + 3zy) =

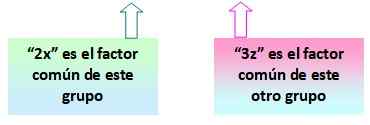
= 2x (x+y) - 3z (x+y)

YoMGORTANTE: O sinal negativo também é um fator comum que deve ser levado em consideração.

Pode servir a você: espaço vetorial: base e dimensão, axiomas, propriedades

Agora observe que os parênteses (x+y) são repetidos nos dois termos obtidos ao agrupar. Esse é o fator comum que estava procurando.

Etapa 3: fatorize toda a expressão

2x² + 2xy - 3zx - 3zy = (x+y) (2x - 3z)

Com o resultado anterior, o objetivo da fatoração foi alcançado, o que não é outro senão transformar uma expressão algébrica com base em somas e subtração de termos, no produto de dois ou mais fatores, em nosso exemplo, de: (x+ y) e (2x - 3z).

Questões importantes sobre o fator de grupo comum

Questão 1: Como saber que o resultado está correto?

Responder: Propriedade distributiva é aplicada ao resultado obtido e, após a redução e simplificação, a expressão assim alcançada deve coincidir com o original, se não, há um erro.

No exemplo anterior, funciona revertido com o resultado, para verificar se está bem:

(x+y) (2x - 3z) = 2x² -3zx +2xy - 3zy

Como a ordem dos adendos não altera a soma, após a aplicação da propriedade distributiva, todos os termos originais, existem sinais incluídos, portanto, a fatoração está correta.

Questão 2: Você poderia ter agrupado de outra maneira?

Responder: Existem expressões algébricas que admitem mais de uma forma de agrupamento e outras que não. No exemplo selecionado, o leitor pode tentar outras possibilidades, por exemplo, agrupamento:

2x² + 2xy - 3zx - 3zy = (2x²- 3zx) + (2xy - 3zy)

E você pode ver que o resultado é o mesmo que obtido aqui. Encontrar o grupo ideal é uma questão de prática.

Pode servir a você: derivado de cotangent: cálculo, demonstração, exercícios

Questão 3: Por que é necessário obter fator comum de uma expressão algébrica?

Responder: Porque existem aplicações nas quais a expressão fatorizada facilita os cálculos. Por exemplo, suponha que você queira fazer 2x² + 2xy - 3zx - 3zy igual a 0. Quais seriam as possibilidades?

Para responder a essa preocupação, a versão fatorizada é muito mais útil do que o desenvolvimento original em termos. Surge assim:

(x+y) (2x - 3z) = 0

Uma possibilidade de que a expressão vale 0 é que x = -y, independentemente do valor de z. E o outro é que x = (3/2) z, sem importar o valor de y.

Exercícios

- Exercício 1

Obtenha um fator comum da seguinte expressão agrupando os termos:

AX+AY+BX+por

Solução

Os dois primeiros estão agrupados, com o fator comum "A" e os dois últimos com o fator comum "B":

ax+ay+bx+por = a (x+y)+b (x+y)

Uma vez feito isso, um novo fator comum é revelado, que é (x+y), de modo que:

ax+ay+bx+por = a (x+y)+b (x+y) = (x+y) (a+b)

Outra maneira de agrupar

Esta expressão admite outra maneira de agrupar. Vamos ver o que acontece se os termos forem reorganizados e um grupo é feito com o qual eles contêm X e outro com aqueles que contêm e:

ax +ay +bx +por = ax +bx +ay +por = x (a +b) +y (a +b)

Dessa maneira, o novo fator comum é (a+b):

ax+ay+bx+por = ax+bx+ay+por = x (a+b)+y (a+b) = (x+y) (a+b)

Isso leva ao mesmo resultado da primeira maneira de agrupar que foi testado.

- Exercício 2

É necessário escrever a seguinte expressão algébrica como o produto de dois fatores:

3º³ - 3º²B+9AB²-para²+AB-3B²

Pode servir a você: coplanares pontos: equação, exemplo e exercícios resolvidos

Solução

Esta expressão contém 6 termos. Vamos tentar agrupar o primeiro e o quarto, o segundo e o terceiro e finalmente o quinto e o sexto:

3º³ - 3º²B+9AB²-para²+AB-3B² = (3º³ -para²) + (- 3º²B+9AB²) + (AB-3B²)

Agora, cada parêntese é fator:

= (3º³ -para²) + (- 3º²B+9AB²) + (Ab -3b²) = a² (3a -1) + 3ab (3b -a) + b (a -3b)

À primeira vista, parece que a situação foi complicada, mas o leitor não deve ser desencorajado, pois vamos reescrever o último mandato:

para² (3a -1) + 3ab (3b -a) + b (a -3b) = a² (3a - 1) + 3ab (3b -a) - b (3b -a)

Os dois últimos termos agora têm um fator comum, que é (3b-a), para que eles possam ser fatorados. É muito importante não perder de vista o primeiro mandato para² (3a - 1), que deve continuar a acompanhar tudo como adicionar, para que você não esteja trabalhando com ele:

para² (3a - 1) + 3ab (3b -a) - b (3b -a) = a² (3a-1) + (3b-a) (3ab-b)

A expressão foi reduzida para dois termos e um novo fator comum é descoberto no último, que é "b". Agora permanece:

para² (3a-1) + (3b-a) (3ab-b) = a² (3a-1) +b (3b-a) (3a-1)

O próximo fator comum na aparição é o 3º - 1:

para² (3a - 1) +b (3b -a) (3a -1) = (3a - 1) [a² + B (3b-A)]

Ou se você preferir sem colchetes:

(3º - 1) [A² + B (3b -a)] = (3a - 1) (a² -AB + 3B²)

O leitor pode encontrar outra maneira de agrupar que leva a esse mesmo resultado?

Figura 2. Exercícios de fatoração propostos. Fonte: f. Zapata.

Referências

1. Baldor, a. 1974. Álgebra Elementar. Cultural venezuelana s.PARA.
2. Jiménez, r. 2008. Álgebra. Prentice Hall.
3. Principais casos de fatoração. Recuperado de: julioprofe.líquido.
4. Unam. Matemática Básica: Fatorização agrupando Termos. Faculdade de Contabilidade e Administração.
5. Zill, d. 1984. Álgebra e trigonometria. MacGraw Hill.