Características fatoriais comuns, exemplos, exercícios

Ele fator comum de uma expressão algébrica é uma quantidade presente em todos os termos disso. Quando o fator comum é conhecido, é possível escrever a expressão de maneira equivalente através de um produto de fatores.

Nem todas as expressões algébricas têm um fator comum, há apenas aqueles que só podem ser divididos entre eles e 1, portanto, não é possível escrevê -los como um produto de fatores. Um exemplo de expressão que não tem fator comum é:

x + y

figura 1. O fator comum de uma expressão algébrica o torna o produto indicado de dois fatores. Fonte: Pixabay.

Em vez disso, sim:

5a + 10b

Visto que os 5 estão presentes em ambos os termos, pois 10 = 5 ∙ 2. Como 5 é o fator comum, o seguinte pode ser escrito:

5a + 10b = 5 ∙ (a + 2b)

O leitor pode verificar através da propriedade distributiva, que a expressão à direita é igual ao original.

O fator comum também pode ser literal ou uma combinação de números e letras, por exemplo, em 4x² - 2x. O x e ele 2 Eles estão entre os fatores e a expressão permanece como um produto:

4x² -2x = 2x⋅ (x -1)

A vantagem de encontrar o fator comum de uma expressão e escrevê -lo como um produto é que quase sempre é fácil operar com ele. É por isso que é usado em muitos procedimentos algébricos e de cálculo, como:

-Ao resolver equações, cujas soluções são rapidamente reveladas quando o fator comum é encontrado.

-Ao calcular um limite com uma indeterminação, isso pode desaparecer ao fatorar adequadamente.

-A fatoração apropriada também facilita as operações com expressões algébricas racionais, como somas e subtrações.

[TOC]

Características fatoriais comuns

As principais características do fator comum são as seguintes:

-Pode ser um número, uma expressão algébrica ou uma combinação de ambos.

-O fator comum deve estar contido em cada um dos termos da expressão para faturar.

Pode atendê -lo: funções transcendentes: tipos, definição, propriedades, exemplos

-De acordo com a quantidade de termos que ele contém, pode ser o caso de:

1. Fator monomial comum, se o fator comum for de um único termo,
2. Fator binomial comum se você tiver dois termos e
3. Fator polinomial comum, se o fator comum consistir em vários termos.

Como encontrar o fator comum de uma expressão algébrica?

Para encontrar o fator comum presente em um polinômio, você deve calcular o divisor comum máximo ou MCD dos coeficientes numéricos de todos os termos, bem como as letras ou literais de cada termo e escolher o poder com o menor expoente.

As cartas ou literais podem ser apresentados como monômios, binômios ou polinômios, como será visto nos seguintes exemplos.

O mais recomendado para entender o processo de obtenção do fator comum é seguir os exemplos e a prática de resolver vários exercícios em cada caso.

Exemplos de fatores comuns

Não devemos perder de vista o fato de que o objetivo do fator comum é convertido uma expressão em um produto indicado de fatores. Então os casos mais relevantes são analisados:

Fator monomial comum

Você tem os seguintes monômios (expressões algébricas de um termo único):

2x²; 10x⁴e; 100x⁶e²

Qual pode ser o fator comum para os três?

Começando com os coeficientes numéricos: 2, 10 e 100, todos são pares e seu MCD é 2. Quanto à parte literal, a variável x está presente nos três termos, e a menor potência é x², Então o fator comum é 2x².

Os três termos propostos podem ser escritos como produtos desse fator dessa maneira:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²e

100x⁶e²= 2x²∙ 50x⁴e²

Multiplicando os fatores à direita, pode -se verificar se o termo da esquerda é obtido.

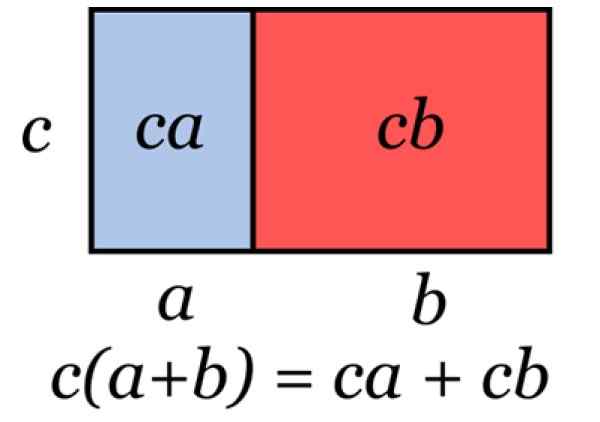Figura 2. Ilustração que representa o fator comum. Fonte: Wikimedia Commons.

Esta técnica é aplicada quando é necessária para levar em consideração uma expressão algébrica, como nos seguintes exemplos:

• Exemplo 1

Fato a seguinte expressão:

Pode servir a você: Isoceles Triangle

5x³e + 10x²e² + 5xy²

O MCD dos coeficientes numéricos de cada termo é:

MCD (5.10) = 5

Quanto à parte literal, tanto o x como a e Eles estão presentes nos três termos e o menor expoente de cada um é 1, portanto o fator comum é 5xy E você pode escrever:

5x³e + 10x²e² + 5xy²= 5xy ∙ (x² +2xy²+e)

Fator polinomial comum

O fator comum pode consistir em um binomial, um trinomial ou em geral em um polinômio. Nesse caso, as instruções na seção anterior ainda são válidas, escolhendo como um fator comum aquele com o menor expoente.

• Exemplo 2

Escreva a seguinte expressão como o produto de dois fatores:

2a (x - 1) - 3b (x - -1)

Por inspeção direta, o fator comum é o binomial (X-1), então:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2a - 3b)

Fatoração agrupando termos

Às vezes, a existência de um fator comum não é evidente, mas é revelada se os termos forem agrupados de maneira conveniente:

• Exemplo 3

Fature 3x³ - 9ax² - x + 3a

À primeira vista, não há fator comum nesses quatro termos, pois, por exemplo, o x Está presente nos três primeiros, mas não no último. E a para É no segundo e no último nada mais.

Quanto aos coeficientes, há três termos em que os 3 estão presentes, no entanto, para ser um fator comum, deve ser em todos os termos.

Parece que as técnicas descritas não podem ser aplicadas desta vez. No entanto, a expressão pode estar considerando agrupando os dois primeiros termos e os dois últimos, tomando cuidado ao colocar os parênteses, para que os sinais sejam apropriados para não alterar o original:

Pode atendê -lo: componentes retangulares de um vetor (com exercícios)

3x³ - 9ax² - x + 3a = (3x³ - 9ax²) - (x - 3a)

Observe o sinal negativo no meio dos parênteses: é necessário, porque, caso contrário, a expressão original mudaria.

Nos parênteses esquerdos, o fator comum é 3x², portanto:

(3x³ - 9ax²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

E observa -se que um fator comum já apareceu: (x - 3a), Isto é, é fator pela segunda vez obter:

3x² (x- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Exercícios fatoriais comuns

Exercício 1

Resolva a equação 4x³ +7x²  +6x = 0

Solução

"X" é um fator comum, portanto:

3x³ -5x²  +2x = x (3x² −5x +2) = 0

Para a expressão à esquerda, é 0, basta que uma dessas duas condições seja atendida:

x = 0

QUALQUER:

3x² −5x +2 = 0

Esta é uma equação completa do segundo grau que pode ser resolvida aplicando a fórmula geral, também usando uma calculadora científica ou outro método algébrico. As soluções desta equação são:

x = 1

x = 2/3

Uma vez encontrado, é ilustrativo escrever a equação como o produto de 3 fatores, embora a declaração não tenha pedido. Seria assim:

x⋅ (x-1) ⋅ (x-2/3) = 0

Exercício 2

Calcule o seguinte limite se houver:

Solução

Primeiro, é substituído em x = −2 para tentar avaliar o limite, ao fazer isso é obtido:

Como é uma indeterminação do formulário 0/0, você deve ser fator para tentar eliminá -lo. O denominador não pode ser fator, mas o numerador faz.

No numerador, o fator comum é x:

x²+2x = x ∙ (x+2)

A expressão fatorizada é substituída no limite e dessa maneira a indeterminação desaparece:

Conclui -se que o limite existe e vale -2.

Referências

1. Baldor, a. 2005. Álgebra. Grupo de pátria cultural.
2. Jiménez, r. 2008. Álgebra. Prentice Hall.
3. Larson, r. 2012. Pré -cálculo. 8º. Edição. Cengage Learning.
4. Stewart, J. 2007. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
5. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.