Existem triângulos escalenos com um ângulo reto?

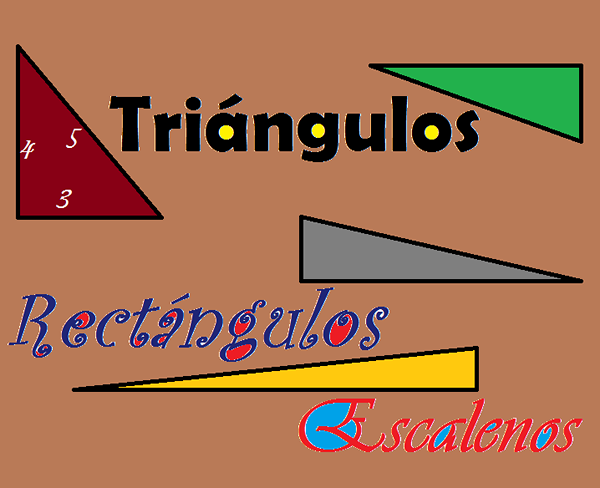
Existem muitos triângulos de Scalele com um ângulo reto. Antes de avançar sobre o assunto, é necessário conhecer os diferentes tipos de triângulos que existem. Os triângulos são classificados por duas classes: seus ângulos internos e os comprimentos de seus lados.

A soma dos ângulos internos de qualquer triângulo é sempre igual a 180º. Mas, de acordo com os ângulos internos, as medidas são classificadas como:

-Acutangle: Esses triângulos são tais que seus três ângulos são agudos, ou seja, medem menos de 90 ° cada.

-Retângulo: Eles são aqueles triângulos que têm um ângulo reto, ou seja, um ângulo que mede 90 ° e, portanto, os outros dois ângulos são agudos.

-Obtuso: Eles são os triângulos que têm um ângulo obtuso, ou seja, um ângulo cuja medida é maior que 90 °.

Triângulos de Scalan com um ângulo reto

O interesse nesta parte é determinar se um triângulo scalene pode ter um ângulo reto.

Como dito acima, um ângulo reto é um ângulo cuja medida é 90º. É necessário apenas conhecer a definição de um triângulo escaleno, que depende do comprimento dos lados de um triângulo.

Classificação de triângulos de acordo com os lados

De acordo com a duração de seus lados, os triângulos são classificados como:

-Equilátero: Eles são todos aqueles triângulos de modo que os comprimentos de seus três lados são iguais.

-Isósceles: Eles são os triângulos que têm exatamente dois lados de igual tempo.

-Escaleno: Eles são aqueles triângulos nos quais os três lados têm medidas diferentes.

Formulação de uma pergunta equivalente

Uma pergunta equivalente à do título é “existem triângulos que têm todos os três lados com medidas diferentes e isso tem um ângulo de 90 °?"

A resposta como declarado no começo é sim. Não é muito difícil justificar esta resposta.

Se cuidadosamente observado, nenhum triângulo retângulo é equilátero, isso pode ser justificado graças ao teorema de Pitágoras por triângulos de retângulo, que diz:

Dado um triângulo retângulo de que os comprimentos de suas categorias são "A" e "B", e o comprimento de sua hipotenusa é "C", você precisa c² = a²+b², que pode ser visto que o comprimento da hipotenusa " C "é sempre maior que o comprimento de cada perna.

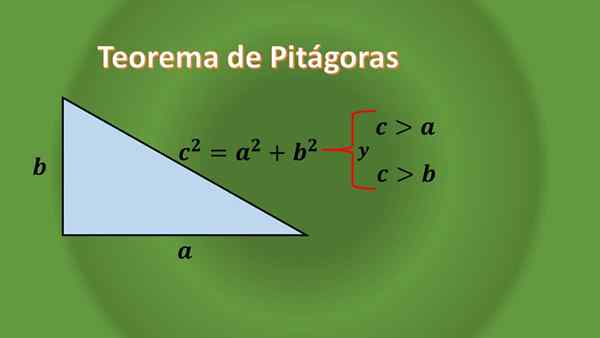
Como nada é dito sobre "A" e "B", isso implica que um triângulo certo pode ser isósceles ou scalene.

Em seguida, basta escolher qualquer triângulo retângulo de modo que suas pernas tenham medidas diferentes e, portanto, um triângulo escaleno que tem um ângulo reto terá sido escolhido.

Exemplos

-Se um triângulo retângulo for considerado cujas pernas têm comprimentos de 3 e 4, respectivamente, então pelo teorema de Pitágoras, pode -se concluir que a hipotenusa terá um comprimento de 5. Isso implica que o triângulo é escaleno e tem um ângulo reto.

-Seja ABC um triângulo retângulo com medidas de medidas 1 e 2. Então o comprimento de sua hipotenusa é √5, que conclui que o ABC é um triângulo retângulo Scaleno.

Nem todo triângulo de escala tem um ângulo reto. Você pode considerar um triângulo como o da figura a seguir, que é escaleno, mas nenhum de seus ângulos internos é reto.

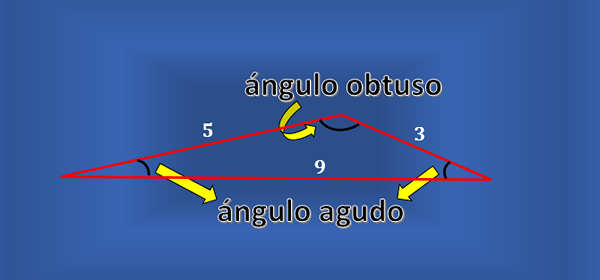Além disso, nem todo triângulo certo é scalene. Se você considerar um triângulo certo cujas pernas medem ambos 1, então a hipotenusa terá uma medida de √2. Portanto, o triângulo retângulo é isósceles.