Erro de estimativa padrão como calculado, exemplos, exercícios

Ele Erro de estimativa padrão Meça o desvio em um valor populacional de amostra. Isto é, o erro de estimativa padrão mede as possíveis variações da média da amostra em relação ao valor verdadeiro da média da população.

Por exemplo, se você quiser saber a idade média da população de um país (média da população), um pequeno grupo de habitantes é levado, que chamaremos de "shows". A partir dela, a idade média (média da amostra) é extraída e supõe -se que a população tenha essa idade média com um erro de estimativa padrão que varia mais ou menos.

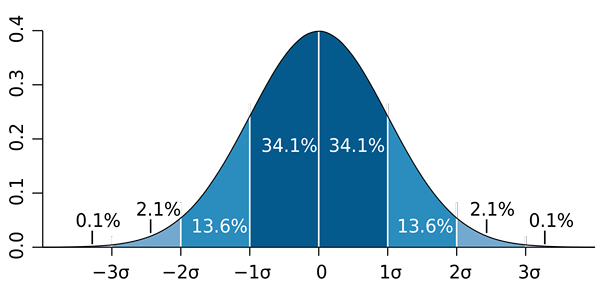
M. C. Toews [CC por 2.5 (https: // CreativeCommons.Org/licenças/por/2.5)]

Deve -se notar que é importante não confundir o desvio padrão com o erro padrão e o erro de estimativa padrão:

1- O desvio padrão é uma medida de dispersão de dados; isto é, é uma medida da variabilidade populacional.

2- O erro padrão é uma medida da variabilidade da amostra, calculada com base no desvio padrão da população.

3- O erro de estimativa padrão é uma medida do erro que é cometido ao tomar a média da amostra como uma estimativa da média da população.

[TOC]

Como é calculado?

O erro de estimativa padrão pode ser calculado para todas as medidas obtidas nas amostras (por exemplo, erro médio de estimativa padrão ou erro padrão da estimativa de desvio padrão) e mede o erro que é cometido ao estimar a medida da população verdadeira a partir de seu valor de amostra

A partir do erro de estimativa padrão, o intervalo de confiança da medida correspondente é construído.

Pode atendê -lo: Matriz reversa: cálculo e exercício resolvido

A estrutura geral de uma fórmula para o erro de estimativa padrão é a seguinte:

Erro de estimativa padrão = ± coeficiente de confiança * Erro padrão

Coeficiente de confiança = Valor limite de uma estatística de amostra ou distribuição de amostragem (Normal ou Gauss Bell, Student T, entre outros) para um certo intervalo de probabilidades.

Erro padrão = desvio padrão da população dividida pela raiz quadrada do tamanho da amostra.

O coeficiente de confiança indica a quantidade de erros padrão que estão dispostos a adicionar e subtrair adaptados para ter um certo nível de confiança nos resultados.

Exemplos de cálculo

Suponha que você esteja tentando estimar a proporção de pessoas na população que têm um comportamento A, e você deseja ter 95% de confiança em seus resultados.

Uma amostra de n pessoas é coletada e a proporção de amostra P e seu complemento q é determinado.

Erro de estimativa padrão (EEE) = ± coeficiente de confiança * Erro padrão

Coeficiente de confiança = z = 1.96.

Erro padrão = a raiz quadrada do motivo entre o produto da proporção da amostra para seu complemento e o tamanho da amostra n.

A partir do erro padrão da estimativa, o intervalo em que a proporção da população ou a proporção da amostra de outras amostras que podem ser formadas a partir dessa população é estabelecida, com 95% de nível de confiança:

P -EEE ≤ proporção populacional ≤ P + Eee

Exercícios resolvidos

Exercício 1

1- Suponha que você esteja tentando estimar a proporção de pessoas na população que preferem uma fórmula de laticínios enriquecidos, e você deseja ter 95% de confiança em seus resultados.

Pode atendê -lo: divisão sintética

Uma amostra de 800 pessoas é coletada e é determinado que 560 pessoas na amostra têm preferência pela fórmula de laticínios enriquecidos. Determine um intervalo em que a proporção da população pode ser esperada e a proporção de outras amostras que podem ser retiradas da população, com 95% de confiança

a) Vamos calcular a proporção da amostra P e seu complemento:

P = 560/800 = 0.70

Q = 1 -P = 1 -0.70 = 0.30

b) Sabe -se que a proporção se aproxima de uma distribuição normal para amostras de tamanho grande (maior que 30). Então, a regra 68 - 95 - 99 chamada é aplicada.7 e você tem que:

Coeficiente de confiança = z = 1.96

Erro padrão = √ (p*q/n)

Erro de estimativa padrão (EEE) = ± (1.96)*√ (0.70)*(0.30)/800) = ± 0.0318

c) A partir do erro de estimativa padrão, o intervalo em que a proporção da população é esperada com o nível de confiança de 95%:

0.70 -0.0318 ≤ proporção populacional ≤ 0.70 + 0.0318

0.6682 ≤ proporção populacional ≤ 0.7318

Você pode esperar a proporção de 70% da amostra para mudar até 3.18 pontos percentuais se for necessário uma amostra diferente de 800 indivíduos ou que a proporção real da população está entre 70 - 3.18 = 66.82% e 70 + 3.18 = 73.18%.

Exercício 2

2- Vamos retirar de Spiegel e Stephens, 2008, o seguinte estudo de caso:

Das graus de matemática total dos primeiros estudantes de ano de uma universidade, foi obtida uma amostra aleatória de 50 qualificações, na qual a média encontrada foi de 75 pontos e o desvio padrão, 10 pontos. Quais são os limites de confiança de 95% para a estimativa da média das qualificações de matemática da universidade?

Pode atendê -lo: qual é a relação entre a área de Rhombus e o retângulo?

a) Vamos calcular o erro de estimativa padrão:

95%de coeficiente de confiança = z = 1.96

Erro padrão = s/√n

Erro de estimativa padrão (EEE) = ± (1.96)*(10√50) = ± 2.7718

b) A partir do erro padrão da estimativa, o intervalo em que a média da população ou a média de outra amostra 50 é estabelecida, com 95% de nível de confiança:

50 -2.7718 ≤ média populacional ≤ 50 + 2.7718

47.2282 ≤ Média populacional ≤ 52.7718

c) Você pode esperar que a média da amostra mude até 2.7718 pontos se uma amostra diferente de 50 graus for tirada ou que a média real dos graus de matemática da população da Universidade esteja entre 47.2282 pontos e 52.7718 pontos.

Referências

1. Abraira, v. (2002). Desvio padrão e erro padrão. Revista Semergen. Web recuperado.Arquivo.org.
2. Rumsey, d. (2007). Estatísticas intermediárias para manequins. Wiley Publishing, Inc.
3. Salinas, h. (2010). Estatística e Probabilidades. Recuperado de Mat.Uda.Cl.
4. Sokal, r.; Rohlf, f. (2000). Biometria. Os princípios e a prática das estatísticas em pesquisa biológica. Terceira ed. Blume Editions.
5. Spiegel, m.; Stephens, l. (2008). Estatisticas. Quarto ed. McGraw-Hill/Interamerican do México S. PARA.
6. Wikipedia. (2019). 68-95-99.7 regra. Recuperado de.Wikipedia.org.
7. Wikipedia. (2019). Erro padrão. Recuperado de.Wikipedia.org.