Fórmulas e equações de equilíbrio rotacional, exemplos, exercícios

Alega -se que um corpo estendido está em balanço rotacional Quando a soma dos torques que agem nela é zero. Isso não significa que o objeto esteja necessariamente em repouso, mas sim que não há tendência líquida para mudar seu estado de movimento para outro.

Um objeto que se move com velocidade constante o faz ao longo de uma linha reta e podemos considerá -lo em equilíbrio rotacional. Agora, os objetos giram porque existem forças que agem sobre eles de tal maneira que é uma rotação. A capacidade de uma força de produzir rotação, chamada torque ou Torca, Depende não apenas da intensidade da força, mas também onde é aplicada.

figura 1. A ponte de suspensão da figura foi projetada para estar em equilíbrio de rotação. Fonte: Wikimedia Commons.

Reconhecemos isso imediatamente quando uma porta fechada será aberta: a força nunca é aplicada perto das dobradiças, mas longe delas, então a alça é colocada o máximo possível, ao lado da porta da porta.

As dobradiças passam o eixo de rotação da porta. Insistindo em empurrá -lo muito perto das dobradiças, você precisa fazer um grande esforço para a porta se mover um pouco.

Na literatura está o torque com nomes diferentes: Momento de torção, torção, momento de uma força e torca. Todos são sinônimos.

Portanto, precisamos saber os torques que agem em um objeto para estabelecer a condição de equilíbrio de rotação.

[TOC]

Condição do equilíbrio rotacional

A condição de equilíbrio rotacional é:

A soma de todos os momentos ou torques que agem em um corpo, calculada em relação a qualquer eixo, deve ser anulada.

O objeto em questão deve ser estendido, uma vez que as partículas, por definição, têm apenas o equilíbrio de tradução.

Você pode atendê -lo: Segunda Lei de Newton: pedidos, experimentos e exercícios

Pode ser aplicado forças no corpo e ainda há um equilíbrio rotacional, enquanto as forças não o giram.

Também pode haver movimento, mesmo acelerado, mas sempre ao longo de uma linha reta, pois nem todas as forças causam a aparência de torques. Eles aparecem quando as forças não agem o tempo todo.

Torque ou momento de força

O torque é indicado com as letras gregas τ, em negrito Porque é um vetor e o distinguimos de sua magnitude ou módulo, que é um escalar. Depende da força aplicada F, do vetor r que é direcionado para o eixo de rotação ou para o ponto de aplicação da força e, finalmente, do ângulo entre esses dois vetores.

A relação adequada entre essas magnitudes é estabelecida através do produto vetorial:

τ = r x F

E o módulo de torque, indicado sem negrito é:

τ = r⋅f⋅sen θ

Onde θ é o ângulo entre r e F. As unidades de torque são simplesmente N⋅m no sistema internacional.

Na figura, há uma chave em inglês com a qual se destina. Para isso, duas forças são tentadas F_PARA e F_B.

F_PARA está mais próximo de O e tem um vetor r_PARA ou braço de alavanca mais curto, portanto não produz tanto torque e força F_B, Que tem a mesma magnitude, mas tem um vetor r_B maior.

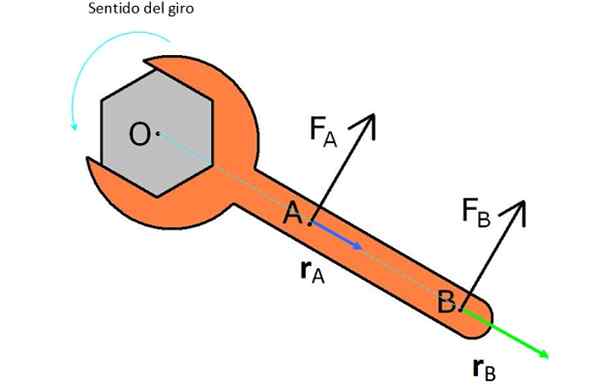Figura 2. Forças e braços aplicados a uma chave em inglês para transformá -la ao contrário das agulhas do relógio. Fonte: Wikimedia Commons.

Observe que, se você deseja girar a porca em um cronograma, deve aplicar as forças na direção oposta à forma como elas aparecem na figura.

Direção e senso de torque

À medida que o torque resulta do produto cruzado entre os vetores de força e posição, e estes estão no plano da chave inglesa, o torque deve ser um vetor perpendicular a esse plano, ou seja, direcionado para o leitor ou dentro da página.

Pode servir a você: pressão atmosférica: valor normal, como é medido, exemplos

Por convenção, o torque é positivo se produzir gira na direção oposta das agulhas do relógio e negativo se o fizer na direção do relógio.

A direção e a direção do torque resultante são facilmente determinadas pela regra da mão direita mostrada abaixo:

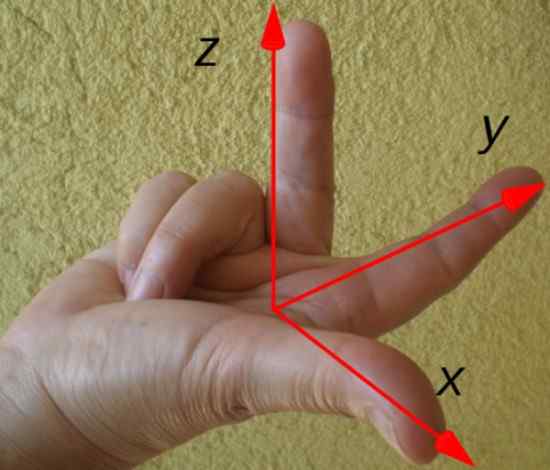Figura 3. Regra da mão direita para determinar a direção e a direção do troca. Fonte: Wikimedia Commons.

Os pontos de dedo indicadores de acordo com o vetor de posição r, O dedo médio de acordo com a força F E o polegar sinaliza a direção e a direção do torque τ. Neste exemplo, o torque é direcionado ao longo do eixo x, de acordo com o desenho dos eixos de coordenadas.

Fórmulas e equações

Se os torques agirem em um corpo τ₁, τ_2, τ_3… τ_Yo, A rede ou torque resultante τ_n É a soma vetorial de todos eles:

τ_n = τ₁+ τ₂ +  τ₃ +_.. τ_Yo

Com o somatório da soma, permanece:

τ_n = ∑ τ_Yo

A condição de equilíbrio é expressa matematicamente da seguinte maneira:

τ_n = 0

O bem:

∑ τ_Yo = 0

Onde o torque τ, Em relação a um certo eixo O, é calculado por:

τ = r x F

E cuja magnitude é:

τ = r⋅f⋅sen θ

Exemplos

-Em humanos e animais, o peso é uma força que pode causar torque, girar e cair.

As pessoas geralmente mantêm tal posição que, ao caminhar, as mantém em equilíbrio de rotação, a menos que a atividade esportiva seja praticada, como ginástica, patinação ou esportes em geral.

-Duas crianças que conseguiram permanecer horizontal no Rocker qualquer sobe e desce Eles estão em equilíbrio de rotação.

-Quando os pires da balança são equilibrados, o sistema está em equilíbrio rotacional.

-Avisos e semáforos que pendem nas ruas e avenidas também estão em equilíbrio rotacional. Se os cabos que os seguem estiverem quebrados, esse equilíbrio será perdido e o aviso está pendurado ou cai.

Pode atendê -lo: aceleração média: como é calculado e resolvido

-Pontes penduradas como Golden Gate em São Francisco e a ponte da Figura 1.

Exercício resolvido

A barra apoiada por um suporte mostrado na figura é muito leve. A força exercida pelo apoio é F e no final a força se aplica PARA.

É solicitado a calcular as magnitudes dessas forças, considerando que o sistema está em equilíbrio de tradução e rotação.

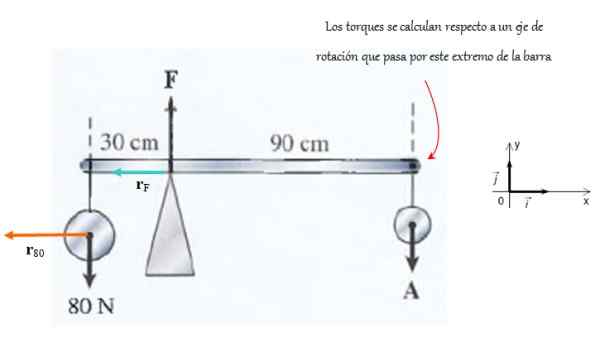Figura 4. Nesta barra, as forças agem de tal maneira que permanece em equilíbrio rotacional. Fonte: f. Zapata.

Solução

À medida que o sistema não se move, a soma das forças é cancelada. Todos são verticais e você pode trabalhar com as magnitudes. O sentido positivo está subindo e o negativo para baixo, portanto:

F - 80 - a = 0

Agora a condição de equilíbrio rotacional é aplicada, para a qual você deve escolher um eixo de rotação arbitrário. Nesse caso, é escolhido no final à direita, para que o vetor r_PARA Seja nulo, dessa maneira o torque exercido por PARA, Mas apenas os de F e a força da esquerda.

O torque produzido por F É, de acordo com a regra da mão direita e o sistema de coordenadas mostrado:

τ_F = r_F x F = 0.9 F (-k) N.m

É direcionado na tela e tem um sinal negativo. Enquanto o torque produzido pela força de 80 n é:

τ = 80 x 1.vinte (k) N⋅m = 96 (k) N⋅m

Este torque é direcionado para fora da tela e recebe um sinal positivo. Como há equilíbrio rotacional:

96 - 0.9⋅f = 0

A magnitude de F é:

F = (96/0.9) n = 106.7 n

E como o sistema está em equilíbrio de tradução, a soma das forças é cancelada. Isso nos permite limpar a magnitude de PARA:

F - a - 80 n = 0

Portanto:

A = 106.7 - 80 n = 26.7 n.

Referências

1. Rex, a. 2011. Fundamentos da Física. Pearson.
2. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.
3. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1. Pearson.
4. Tipler, p. (2006) Física para ciência e tecnologia. 5ª ed. Volume 1. Editorial revertido.
5. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. McGraw Hill.