Equações polinômicas

O que são equações polinomiais?

As Equações polinômicas Eles são uma declaração que levanta a igualdade de duas expressões ou membros, onde pelo menos um dos termos que compõem cada lado da igualdade são polinômios p (x). Essas equações são nomeadas de acordo com o grau de suas variáveis.

Em geral, uma equação é uma afirmação que estabelece a igualdade de duas expressões, onde em pelo menos uma delas existem quantidades desconhecidas, que são chamadas de variáveis ​​ou desconhecidas. Embora existam muitos tipos de equações, geralmente são classificados em dois tipos: algébrica e transcendente.

As equações polinômicas contêm apenas expressões algébricas, que podem ter uma ou mais incógnitas que intervêm na equação. De acordo com o expoente (grau) que eles têm, eles podem ser classificados como: primeira série (linear), segunda série (quadrática), terceira série (cúbica), quarta série (quântica), de grau maior ou igual a cinco e irracional.

Características das equações polinomiais

Equações polinômicas são expressões formadas por uma igualdade entre dois polinômios; Isto é, para as somas finitas de multiplicações entre valores desconhecidos (variáveis) e números fixos (coeficientes), onde as variáveis ​​podem ter expoentes, e seu valor pode ser um número inteiro positivo, incluindo zero.

Os expoentes determinam o grau ou tipo de equação. Esse termo da expressão que tem mais expoente de valor representará o grau absoluto de polinomial.

As equações polinômicas também são conhecidas como algébricas, seus coeficientes podem ser números reais ou complexos e as variáveis ​​são números desconhecidos representados por uma letra, como: "X".

Se, ao substituir um valor pela variável "X" em p (x), o resultado é igual a zero (0), é dito que esse valor satisfaz a equação (é uma solução) e geralmente é chamada de raiz polinomial.

Quando uma equação polinomial é desenvolvida, todas as raízes ou soluções querem ser encontradas.

Tipos de equações polinomiais

Existem vários tipos de equações polinomiais, que são diferenciadas de acordo com o número de variáveis, e também de acordo com o seu grau de expoente.

Assim, as equações polinomiais -onde seu primeiro termo é um polinômio que tem apenas um desconhecido, considerando que seu grau pode ser qualquer número natural (n) e o segundo termo é zero -pode ser expresso da seguinte forma:

Pode atendê -lo: História da trigonometria de suas origens

para_{N *} xⁿ + para_{N-1 *} x^N-1 +… + A_{1 *} x¹ + para_{0 *} x₀ = 0

Onde:

• para_n, para_N-1 já₀, São coeficientes reais (números).
• para_n é diferente de zero.
• Expoente n é um número inteiro positivo que representa o grau de equação.
• x é a variável ou desconhecida que deve ser procurada.

O grau absoluto ou maior de uma equação polinomial é o expoente de maior valor entre todos aqueles que se formam polinômios; Dessa forma, as equações são classificadas como:

Primeiro grau

As equações polinomiais do primeiro grau, também conhecidas como equações lineares, são as que o grau (o maior expoente) é igual a 1, o polinômio é da forma p (x) = 0; E é composto por um termo linear e independente. Está escrito da seguinte maneira:

AX + B = 0.

Onde:

• A e B são números reais e A ≠ 0.
• Machado é o termo linear.
• B é o termo independente.

Por exemplo, Equação 13x - 18 = 4x.

Para resolver equações lineares, todos os termos que contêm o X desconhecido devem ser passados ​​para o lado da igualdade, e aqueles que não se movem do outro lado, a fim de limpá -lo e obter uma solução:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

Dessa maneira, a equação dada possui apenas uma solução ou raiz, que é x = 2.

Segundo grau

As equações polinomiais de segundo grau, também conhecidas como equações quadráticas, são aquelas em que o grau (o maior expoente) é igual a 2, o polinômio é da forma p (x) = 0 e é composto por um termo quadrático, a a linear e um independente. É expresso o seguinte:

machado² + BX + C = 0.

Onde:

• a, b e c são números reais e a ≠ 0.
• machado² É o termo quadrático e "a" é o coeficiente do termo quadrático.
• BX é o termo linear e "B" é o coeficiente do termo linear.
• C é o termo independente.

Resolvente

Geralmente, a solução para esse tipo de equações é dada ao limpar X da equação e permanece a seguinte, que é chamada de resolvente:

Pode servir a você: Teorema Binomial

Lá, (b² - 4ac) é chamado de discriminação da equação e essa expressão determina o número de soluções que a equação pode ter:

• Sim B² - 4ac) = 0, a equação terá uma única solução dupla; isto é, terá duas soluções iguais.
• Sim B² - 4ac)> 0, a equação terá duas soluções reais diferentes.
• Sim B² - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Por exemplo, você tem a equação 4x² + 10x - 6 = 0, para resolvê -lo primeiro Os termos A, B e C são identificados e, em seguida, é substituído na fórmula:

A = 4

B = 10

C = -6.

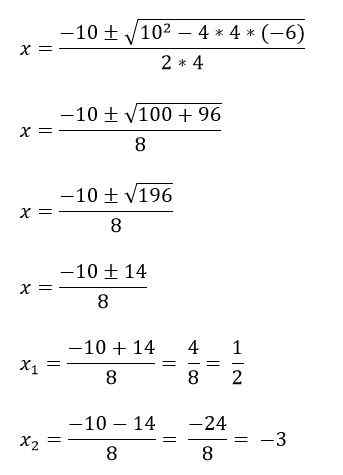
Há casos em que as equações polinomiais de segundo grau não têm os três termos, e é por isso que eles são resolvidos de maneira diferente:

• No caso de as equações quadráticas não terem o termo linear (ou seja, b = 0), a equação será expressa como machado² + C = 0. Para resolvê -lo, x é limpo² E as raízes quadradas são aplicadas em cada membro, lembrando que os dois sinais possíveis que o desconhecido pode ter:

machado² + C = 0.

x² = - c ÷ a

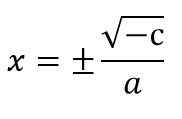
Por exemplo, 5 x² - 20 = 0.

5 x² = 20

x² = 20 ÷ 5

x = ± √4

x = ± 2

x₁ = 2.

x₂ = -2.

• Quando a equação quadrática não tem um termo independente (ou seja, c = 0), a equação será expressa como machado² + Bx = 0. Para resolvê -lo, o fator comum do X desconhecido deve ser tomado no primeiro membro; Como a equação é comparada a zero, é cumprido que pelo menos um dos fatores será igual a 0:

machado² + Bx = 0.

x (ax + b) = 0.

Dessa forma, você tem que:

x = 0.

x = -b ÷ a.

Por exemplo: você tem a equação 5x² + 30x = 0. Primeiro é fator:

5x² + 30x = 0

x (5x + 30) = 0.

São gerados dois fatores que são x y (5x + 30). Um deles será considerado zero e o outro recebe uma solução:

x₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

x₂ = -6.

Mais alto grau

As principais equações polinomiais do grau são aquelas que variam a partir da terceira série, que podem ser expressas ou resolvidas com a equação polinomial geral para qualquer grau:

Pode servir a você: coeficiente de correlação: fórmulas, cálculo, interpretação, exemplo

para_{N *} xⁿ + para_{N-1 *} x^N-1 +… + A_{1 *} x¹ + para_{0 *} x₀ = 0

Isso é usado porque uma equação com um grau maior que dois é o resultado da fatoração de um polinômio; isto é, é expresso como a multiplicação de polinômios de grau um ou maiores, mas sem raízes reais.

A solução desse tipo de equações é direta, porque a multiplicação de dois fatores será igual a zero se algum dos fatores for nulo (0); Portanto, cada uma das equações polinomiais encontradas deve ser resolvida, correspondendo a cada um de seus fatores a zero.

Por exemplo, você tem a equação de terceiro grau (cúbica) x³ + x² +4x + 4 = 0. Para resolvê -lo, você deve seguir as seguintes etapas:

• Os termos são agrupados:

x³ + x² +4x + 4 = 0

(x³ + x² ) + (4x + 4) = 0.

• Os membros se quebram para obter o fator comum do desconhecido:

x² (x + 1) + 4 (x + 1) = 0

(x² + 4)_*(x + 1) = 0.

• Dessa forma, dois fatores são obtidos, que devem ser iguais a zero:

(x² + 4) = 0

(x + 1) = 0.

• Pode -se observar que o fator (x² + 4) = 0 não terá uma solução real, enquanto o fator (x + 1) = 0 sim. Portanto, a solução é:

(x + 1) = 0

x = -1.

Exercícios resolvidos

Resolva as seguintes equações:

Primeiro exercício

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Solução

Nesse caso, a equação é expressa como a multiplicação de polinômios; isto é, é fatorado. Para resolvê -lo, cada fator deve ser igual a zero:

2x² + 5 = 0, não tem solução.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

Dessa maneira, a equação dada possui duas soluções: x = 3 e x = -1.

Segundo exercício

x⁴ - 36 = 0.

Solução

Foi dado um polinômio, que pode ser rescrito como uma diferença nos quadrados para alcançar uma solução mais rápida. Assim, a equação permanece:

(x² + 6)_*(x² - 6) = 0.

Para encontrar a solução das equações, ambos os fatores são iguais a zero:

(x² + 6) = 0, não tem solução.

(x² - 6) = 0

x² = 6

x = ± √6.

Assim, a equação inicial tem duas soluções:

x = √6.

x = - √6.