120 divisores

O 120 divisores Eles são todos aqueles números que dividem exatamente. Esses números são os seguintes:

Divisores de 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

Além disso, os opostos a esse conjunto de números, ou seja, os negativos, são 120 divisores, uma vez que a divisão é exata. Os 120 possuem 16 divisores inteiros positivos e muitos outros negativos.

Existem várias maneiras de encontrar os divisores de um número. Se isso não for muito grande, você pode usar as tabelas de multiplicação (para números inferiores a 100) e verificar em que tabelas o número em questão aparece. Por exemplo, 12 aparecem nas mesas de 2, 3, 4 e 6, e esses são seus divisores, juntamente com 1 e os mesmos 12.

O número também pode ser dividido em seus principais fatores, aplicar as regras de divisibilidade e multiplicar os fatores. Mas você deve ter cuidado para não passar por nenhum divisor esquecido.

Como 120 é maior que 100, não é diretamente nas tabelas de multiplicação, no entanto, não é muito trabalhoso encontrar seus 16. Um procedimento válido para todos os números é mostrado imediatamente, através do uso de tabelas muito simples.

Quantos divisores é 120?

Primeiro, o número de divisores de 120 é descoberto. Há uma fórmula que permite que você saiba quantos você tem, embora não diga o que são.

Números compostos, como 120, podem ser expressos como o produto de números primos, ou poderes destes. Chamando N para qualquer número de composto:

N = aⁿ ∙ b^m ∙ c^p … R^k

Pode atendê -lo: relações de proporcionalidade: conceito, exemplos e exercícios

Os números A, B, C ... R são números primos e os valores de N, M, P, ... K, os respectivos poderes. A decomposição em fatores primos de 120 é a seguinte:

120 | 2
60 | 2
30 | 2
15 | 3
5 | 5
1 | 1

Dessa forma, 120 é o produto dos fatores:

120 = 2³ ∙ 3 ∙ 5

Fórmula para calcular o número de divisores de n

Número de divisores = (n +1) × (m +1) × (p +1)… × (k +1)

Agora a fórmula para 120 é aplicada. Da decomposição em fatores que você precisa:

n = 3 (é o poder de 2)

M = 1 (o 3 é elevado a 1: 3¹ = 3)

P = 1 (o 5 também parece elevado a 1)

Com estes valores:

Número de divisores de 120 = (3 +1) × (1 +1) × (1 +1) = 4 × 2 × 2 = 16

Este resultado coincide com o início do início: 120 tem 16 divisores. Além disso, já se sabe que os 2, 3 e 5 são divisores de 120, bem como 10, já que qualquer número terminado em 0 é divisível por 10. O procedimento para encontrar tudo é mostrado imediatamente.

Cálculo dos divisores de 120

É feito com a ajuda dos fatores calculados na seção anterior. Lá foi visto que o 2 é um fator primitivo com o expoente 3, e o 3 é outro fator de primo, com o expoente 1. Com essas informações, a tabela a seguir é construída:

Observe que os poderes de 2 começam em 2⁰ e terminar em 2³, qual é o fator que surge ao decompor 120. Lembre -se disso 2⁰ e 3⁰ Ambos são iguais a 1 (qualquer número alto a 0 é 1). Para o fator 3, começa em 3⁰ Até 3¹, Desde 3¹ = 3.

Em seguida, a tabela é concluída com o produto dos números em vermelho, como mostrado aqui:

Pode servir a você: inverso multiplicativo: explicação, exemplos, exercícios resolvidos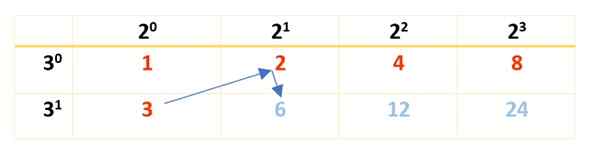

Todos os números vermelhos e azuis são 120 divisores, mas há apenas 8. Para encontrar os restantes, uma nova tabela é estourada, os divisores já obtidos na primeira fila e o fator que ainda precisa ser levado em consideração estão escritos: 5, com seus poderes na primeira coluna, à esquerda, assim:

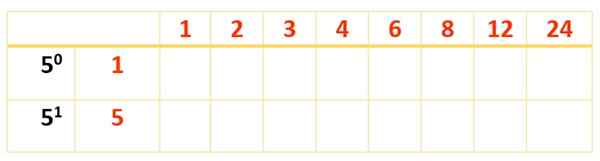
Agora, a tabela é concluída com os produtos dos números em vermelho, como foi feito com a primeira tabela:

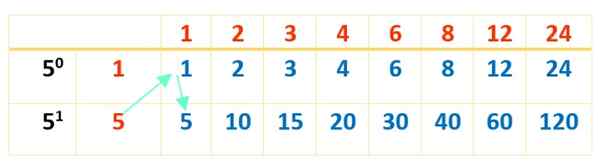
E finalmente os 16 divisores de 120 em azul aparecem. As tabelas são uma excelente ajuda para as operações serem feitas em ordem e, portanto, nenhum divisor 120.

Exercícios resolvidos

O procedimento para encontrar todos os divisores de um número está resumido da seguinte maneira:

1. Divida o número em fatores primos.
2. Calcule o número de divisores com a fórmula.
3. Construa as tabelas necessárias para encontrar divisores. Se o número tiver dois fatores, uma tabela for suficiente, se você tiver três fatores, duas tabelas devem ser feitas, como no caso de 120.

Exercício 1

Encontre todos os divisores de 288.

Solução

288 se decompõe em fatores primos:

288 | 2
144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 | 1

O 288 está escrito assim:

288 = 2⁵ ∙ 3²

Imediatamente é o número de divisores de 288 a:

Número de divisores = (n +1) × (m +1) × (p +1)… × (k +1)

A partir da decomposição em fatores primos, observa -se que n = 5 e m = 2, então:

Divisores de 288 = (5 +1) × (2 +1) = 6 × 3 = 18

Existem 18 divisores e, como existem apenas dois fatores, é suficiente com apenas uma tabela:

Pode atendê -lo: características do retângulo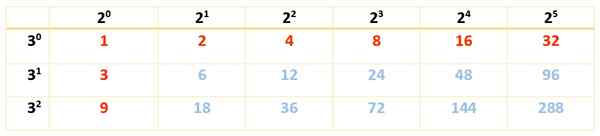

Os divisores de 288 são os números em vermelho e em azul:

Div (288) = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288

Eles podem ser verificados rapidamente com a ajuda de uma calculadora.

Exercício 2

Encontre os divisores de 350

Solução

350 se decompõe:

350 | 2
175 | 5
35 | 5
7 | 7
1 | 1

O 350 pode ser escrito como um produto de três fatores:

350 = 2 ∙ 5²∙ 7

O próximo passo é calcular quantos divisores tem, através da fórmula:

Número de divisores = (n +1) × (m +1) × (p +1)… × (k +1)

Com n = 1, m = 2, p = 1

Divisores de 288 = (1 +1) × (2 +1) × (1 +1) = 2 × 3 × 2 = 12

Como 350 requer três fatores, duas tabelas devem ser feitas. O primeiro é feito com 2 e 5², Mas também pode ser feito com 2 e 7, ou com 7 e 5², De acordo com a preferência, pois em todas as formas, o resultado final é o mesmo:

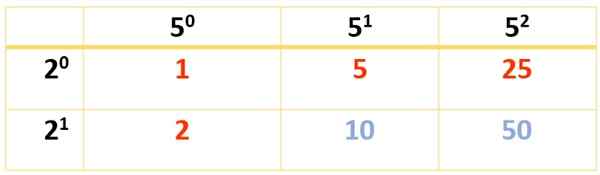
6 divisores são obtidos. Os outros aparecem com a ajuda desta outra tabela:

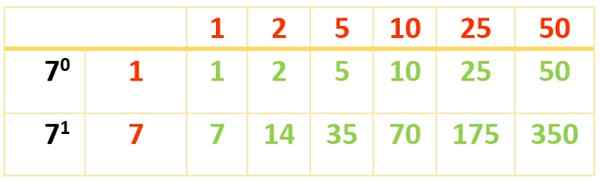
Os divisores de 350 são:

Div (350) = 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350