Divisões em que o resíduo é 300

Existem muitos divisões em que o resíduo é 300. Além de citar alguns deles, será exibida uma técnica que ajuda a construir cada uma dessas divisões, o que não depende do número 300.

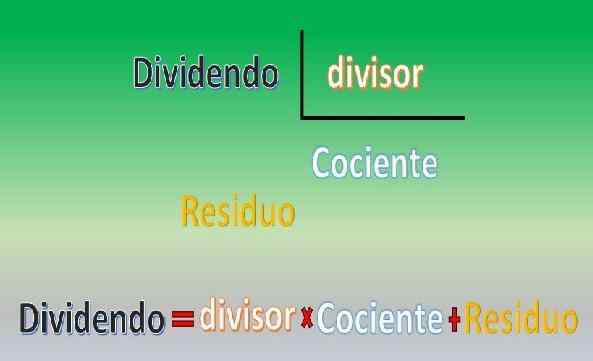
Esta técnica é fornecida pelo algoritmo da divisão Euclides, que estabelece o seguinte: Dos dois números inteiros "n" e "b", com "b" diferente de zero (b ≠ 0), existem "Q" exclusivos e "r ", de modo que n = bq+r, onde 0 ≤" r " < |b|.

Os números "n", "b", "q" e "r" são chamados de dividendo, divisor, quociente e resíduo (ou descanso), respectivamente.

Deve -se notar que, ao exigir que o resíduo seja 300, está sendo dito implicitamente que o valor absoluto do divisor deve ser maior que 300, isto é: | B |> 300.

Exemplos de divisões em que o resíduo é 300

Abaixo estão algumas divisões nas quais o resíduo é de 300; Então, o método de construção de cada divisão é apresentado.

1- 1000 ÷ 350

Se 1000 estiver dividido por 350, pode -se ver que o quociente é 2 e o resíduo é 300.

2-1500 ÷ 400

Dividindo 1500 por 400, obtém -se que o quociente é 3 e o resíduo é 300.

3-3800 ÷ 700

Ao fazer esta divisão, será que o quociente é 5 e o resíduo será 300.

4- 1350 ÷ (−350)

Quando esta divisão é resolvida, -3 como um quociente e 300 como um resíduo.

Como essas divisões são construídas?

Para construir as divisões anteriores, você só precisa usar o algoritmo de divisão corretamente.

As quatro etapas para construir essas divisões são:

1- Defina o resíduo

Como você deseja que o resíduo seja 300, r = 300 está definido.

2- Escolha um divisor

Como o resíduo é 300, o divisor a ser escolhido deve ser qualquer número de tal forma que seu valor absoluto seja maior que 300.

3- Escolha um quociente

Para o quociente, você pode escolher qualquer número diferente de zero (q ≠ 0).

4- dividendo é calculado

Depois que o resíduo, o divisor e o quociente são fixos, eles são substituídos no lado direito do algoritmo de divisão. O resultado será o número que deve ser escolhido como um dividendo.

Com essas quatro etapas simples, você pode ver como cada divisão da lista foi construída. Em todos esses r = 300 foram definidos.

Para a primeira divisão, b = 350 e q = 2 foram escolhidos. Ao substituir o algoritmo de divisão, 1000 foi obtido como resultado. Para que o dividendo deve ser 1000.

Para a segunda divisão, b = 400 e q = 3 foram estabelecidos, de modo que, substituindo o algoritmo da divisão, 1500 foram obtidos. Assim, está estabelecido que o dividendo é 1500.

Para o terceiro, o número 700 foi escolhido como divisor e como quociente, o número 5. Ao avaliar esses valores no algoritmo de divisão, obteve -se que o dividendo deve ser igual a 3800.

Para a quarta divisão, o divisor igual a -350 e o quociente igual a -3. Quando esses valores são substituídos no algoritmo de divisão e resolvidos, é obtido que o dividendo é igual a 1350.

Seguindo essas etapas, muitas outras divisões podem ser construídas nas quais o resíduo é 300, tomando cuidado quando eles querem usar números negativos.

Deve -se notar que o processo de construção descrito acima pode ser aplicado para construir divisões com resíduos diferentes de 300. Somente o número 300 é alterado, na primeira e na segunda etapa, para o número desejado.