Divisão sintética

Explicamos o que é a divisão sintética, um método para fazê -lo, exemplos e exercícios resolvidos.

O que é divisão sintética?

O Divisão sintética É uma maneira simples de dividir um polinomial p (x) por um dos formulários d (x) = x - c - c - c - c - c - c. Por exemplo, Polinomial p (x) = (x⁵+3x⁴-7x³+2x²-8x+1) pode ser representado como a multiplicação dos dois polinômios mais simples (x+1) e (x⁴ + 2x³).

É uma ferramenta muito útil, pois, além de nos permitir dividir polinômios, também permite avaliar um polinômio p (x) em qualquer número C, que por sua vez nos indica com precisão se esse número for zero ou não do polinomial.

Graças ao algoritmo da divisão, sabemos que se tivermos dois P (x) polinomial (x) e D (x) (x) + r (x), onde r (x) é zero ou é menor que q (x). Esses polinômios são conhecidos como quociente e resíduo ou descanso, respectivamente.

Nas ocasiões em que o polinomial d (x) é da forma x - c, a divisão sintética nos dá uma curta maneira de encontrar quem são Q (x) e R (x).

Método da divisão sintética

Seja p (x) = a_nxⁿ+para_N-1x^N-1+… +A₁x+a₀ o polinômio que queremos dividir e d (x) = x-c o divisor. Para se dividir pelo método da divisão sintética, procedemos da seguinte maneira:

1- Nós escrevemos os coeficientes de p (x) na primeira linha. Se qualquer energia x não aparecer, colocamos zero como seu coeficiente.

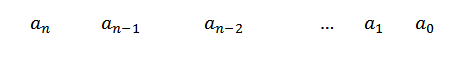
2- na segunda fila, à esquerda de um_n Colocamos C e desenhamos linhas de divisão, como mostrado na figura a seguir:

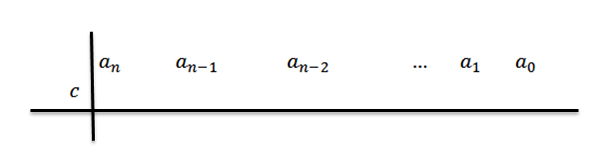
3- Abaixamos o coeficiente principal para a terceira linha.

Pode servir a você: Método Euler: Qual é o uso de procedimento e exercícios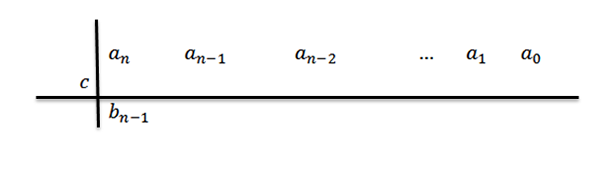

Nesta expressão B_N-1= a_n

4- Nós multiplicamos C pelo coeficiente principal B_N-1 E escrevemos o resultado na segunda fila, mas uma coluna à direita.

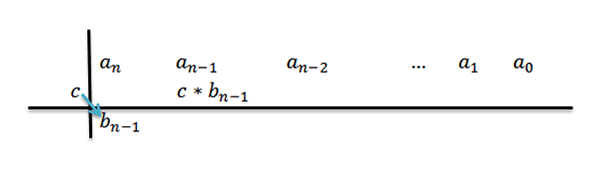
5- Adicionamos a coluna em que escrevemos o resultado anterior e o resultado é colocado sob a referida soma. Isto é, na mesma coluna, terceira fila.

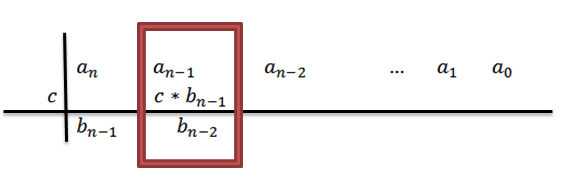
Ao adicionar, temos como resultado_N-1+c*b_N-1, para o qual por conforto chamaremos de B_N-2

6- Nós multiplicamos C pelo resultado anterior e escrevemos o resultado à sua direita na segunda linha.

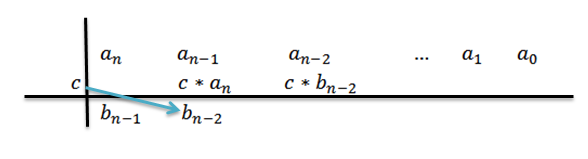
7- Repitamos as etapas 5 e 6 até chegarmos ao coeficiente para₀.

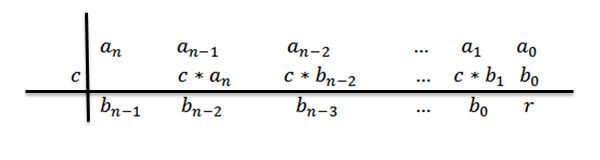
8- Nós escrevemos a resposta, isto é, o quociente e o resíduo. Como estamos fazendo a divisão de um polinômio de grau N entre um polinômio de grau 1, temos que o quociente seria o grau N-1.

Os coeficientes do polinômio quociente serão o número da terceira fila, exceto o último, que será o polinomial de resíduos ou o restante da divisão.

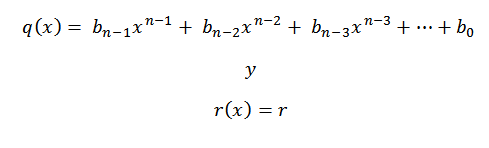
Exercícios resolvidos

Exemplo 1

Faça a seguinte divisão pelo método da divisão sintética:

(x⁵+3x⁴-7x³+2x²-8x+1): (x+1).

Solução

Primeiro, escrevemos os coeficientes de dividendos da seguinte forma:

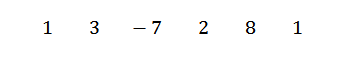
Então escrevemos C no lado esquerdo, na segunda fila, junto com as linhas de divisão. Neste exemplo C = -1.

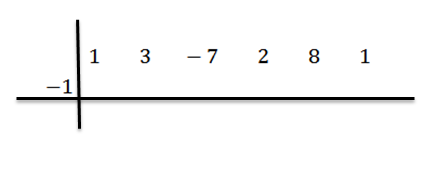
Abaixamos o coeficiente principal (neste caso B_N-1 = 1) e nós multiplicamos por -1:

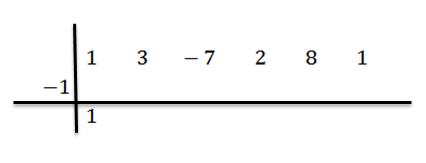
Escrevemos seu resultado à direita na segunda linha, como mostrado abaixo:

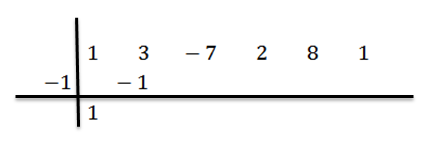
Adicionamos os números da segunda coluna:

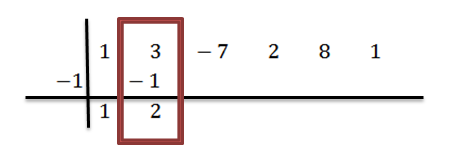
Multiplamos 2 por -1 e escrevemos o resultado na terceira coluna, segunda linha:

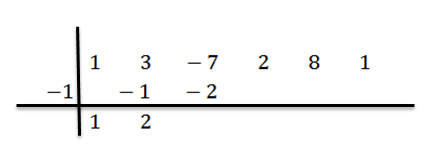
Adicionamos na terceira coluna:

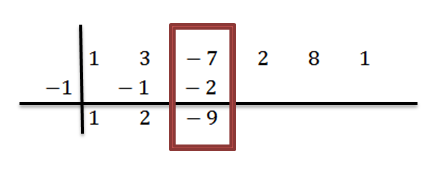
Procedemos analogamente até chegarmos à última coluna:

Pode atendê -lo: abordagem padrão e excesso: o que é e exemplos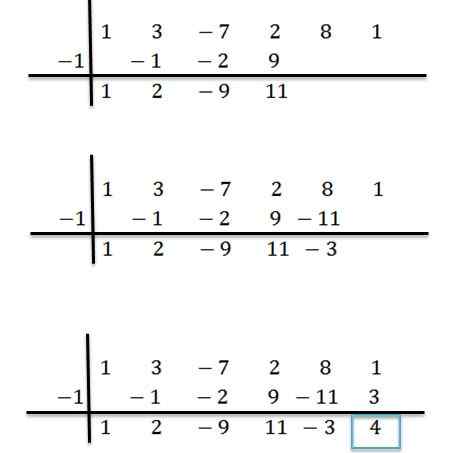

Assim, temos que o último número obtido é o restante da divisão, e os números restantes são os coeficientes do quociente polinômio. Isso está escrito da seguinte maneira:

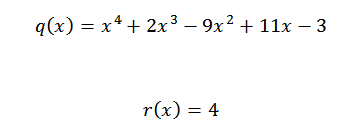
Se queremos verificar se o resultado está correto, basta verificar se a seguinte equação é atendida:

P (x) = q (x)*d (x) + r (x)

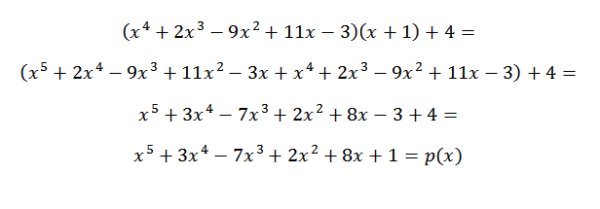
Assim, podemos verificar se o resultado obtido está correto.

Exemplo 2

Realize a seguinte divisão polinomial pelo método da divisão sintética:

(7x³-x+2): (x+2)

Solução

Nesse caso, temos esse termo x² Não aparece, então vamos escrever para 0 como seu coeficiente. Assim, o polinomial permaneceria como 7x³+0x²-x+2.

Escrevemos seus coeficientes seguidos, isto é:

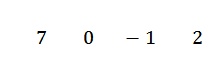
Escrevemos o valor de c = -2 para o lado esquerdo na segunda linha e desenhamos as linhas de divisão.

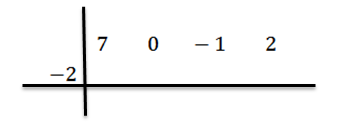
Abaixamos o coeficiente principal B_N-1 = 7 e nós multiplicamos por -2, escrevendo seu resultado na segunda linha à direita.

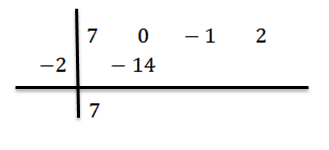
Adicionamos e prosseguimos, como explicado anteriormente, até chegarmos ao último mandato:

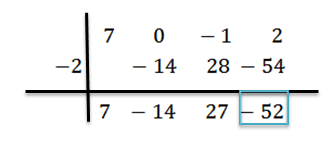
Nesse caso, o resto é r (x) = -52 e o quociente obtido é q (x) = 7x²-14x+27.

Exemplo 3

Outra maneira de usar a divisão sintética é a seguinte.

Para o algoritmo da divisão, podemos escrever o P (x) polinomial da seguinte forma:

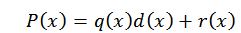
Nesta expressão, q (x) e r (x) são o quociente e o restante, respectivamente. Agora, se d (x) = x-c, ao avaliar em c em polinômio, encontramos o seguinte:

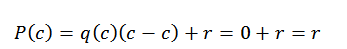
É por isso que resta apenas encontrar r (x), e podemos fazer isso graças à divisão sintética.

Por exemplo, temos polinomial p (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x²-37x-37 e queremos saber qual é o seu valor ao avaliá-lo em x = 5. Para isso, realizamos a divisão entre p (x) e d (x) = x -5 pelo método da divisão sintética:

Pode servir a você: simetria axial: propriedades, exemplos e exercícios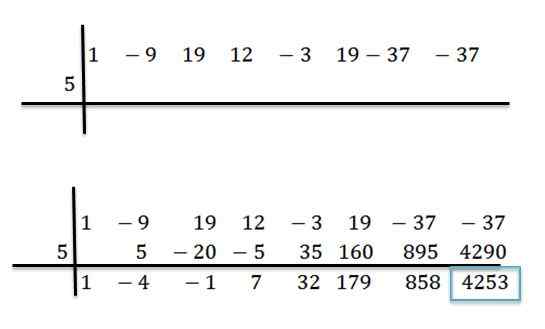

Depois que as operações forem realizadas, sabemos que podemos escrever p (x) da seguinte maneira:

P (x) = (x⁶-4x⁵ -x⁴+ 7x³ +32x² +179x + 858)*(X-5) + 4253

Portanto, ao avaliar, temos que:

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(5-5) +4253

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(0) +4253

P (5) = 0 + 4253 = 4253

Como podemos ver, é possível usar a divisão sintética para encontrar o valor de um polinômio ao avaliá -lo em c em vez de simplesmente substituir C por x. 

Se tentarmos avaliar P (5) da maneira tradicional, precisaríamos de alguns cálculos que geralmente se tornam tediosos.

Exemplo 4

O algoritmo de divisão para polinômios também é atendido para polinômios com coeficientes complexos e, como conseqüência, temos que o método de divisão sintética também funciona para esses polinômios. Em seguida, veremos um exemplo.

Usaremos o método da divisão sintética para mostrar que z = 1+ 2i é zero do polinomial p (x) = x³+ (1+i) x² -(1+2i) x+(15+5i). Isto é, o resíduo da divisão p (x) entre d (x) = x - z é igual a zero.

Procedemos como antes: Na primeira linha, escrevemos os coeficientes de p (x), então no segundo em que escrevemos z e desenhamos as linhas de divisão.

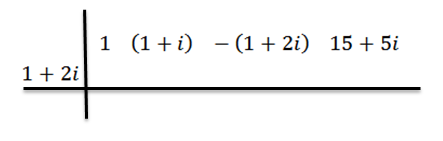
Fazemos a divisão como antes, isso é:

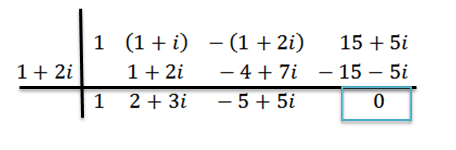
Podemos ver que o resíduo é zero; Portanto, concluímos que z = 1+ 2i é um zero de p (x).

Referências

1. Baldor, Aurelio. Álgebra. Grupo editorial da Patria.
2. Demana, Waits, Foley & Kennedy. Precáculo: gráfico, numérico, algébrico. Pearson Education.