A distribuição uniforme continua características, exemplos, aplicações
- 1515
- 358
- Ernesto Bruen
Uma variável aleatória tem um Distribuição uniforme contínua Se a probabilidade de tomar um valor, dentro de um intervalo finito [a, b], é o mesmo para qualquer subinterval de igual comprimento.
Esta distribuição é análoga à distribuição uniforme discreta, que atribuiu a cada resultado do experimento aleatório a mesma probabilidade, mas neste caso a variável a ser considerada é contínua. Por exemplo, o experimento que consiste em selecionar um número real aleatório, entre os valores A e B, segue a distribuição uniforme. Aqui você tem seu gráfico:
figura 1. Gráfico da função de densidade da distribuição uniforme normalizada contínua Na notação matemática, a distribuição uniforme contínua tem uma função de densidade definida como uma função em peças ou por seções, que podem ser escritas como:
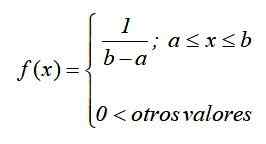
O gráfico desta função, conhecido como Função de curva ou densidade, É um retângulo, então a distribuição uniforme contínua também é conhecida como distribuição retangular E é a mais simples das distribuições contínuas.
A área sob o gráfico de uma distribuição de probabilidades é igual a 1 e sempre leva valores positivos. A distribuição uniforme atende a esses critérios. Não é necessário integrar diretamente para verificar se a área é 1, uma vez que a área do retângulo sombreado na Figura 1 pode ser calculado usando a fórmula:
Área = base x altura = (b - a) x [1/(b - a)] = 1
Conhecer a área sob a curva de densidade é muito importante, porque existe uma relação entre a área e a probabilidade de ocorrência de um evento, que para esta distribuição é determinada na seção a seguir.
Características de distribuição uniforme contínua
A distribuição uniforme contínua é caracterizada por seu:
Função de densidade
Seja x a variável aleatória contínua, que pertence ao intervalo [a, b], então:
Pode servir a você: Transformações lineares: Propriedades, quais são o uso, tipos, exemplos=\frac1b-a)
Função de distribuição
Por meio da função de distribuição, a probabilidade de a variável aleatória x obtém um valor X dos possíveis valores do intervalo [a, b] é calculado. Para uma distribuição contínua, geralmente é calculada dessa maneira:
=\int_a^xf(x)dx)
No caso da distribuição uniforme contínua, a referida probabilidade f (x) é equivalente à área do retângulo cuja base é (x-a) e sua altura é (b-a):
=\int_a^x\left&space;(\frac1b-a&space;\right&space;)dx=\fracx-ab-a)
Matematicamente, se f (x) = pr (x = x), a seguinte função for estabelecida por peças, de acordo com o resultado anterior:
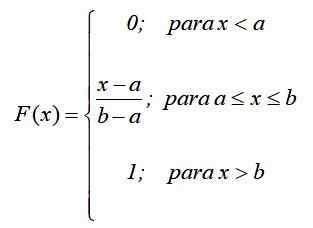
Dessa forma, o que já foi dito antes: a probabilidade depende apenas do valor de (x-a) e não de sua localização no intervalo [a, b]. O gráfico da função de distribuição é:
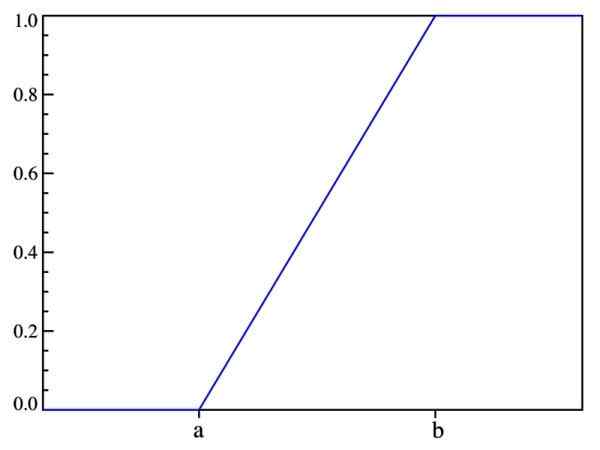Figura 2. Gráfico da função de distribuição F (x). Fonte: Wikimedia Commons. Valor esperado, variação e desvio padrão
Depois de fazer inúmeras experiências com a variável aleatória contínua, seu valor médio é chamado valor esperado, É indicado como E (x) e é calculado pela seguinte integral:
=\int_a^bxf(x)=\int_a^b\left&space;(\frac1b-a&space;\right&space;)xdx=\left&space;(\frac1b-a&space;\right&space;)\frac(b^2-a^2)2=\fraca+b2)
V (x) = e (x2) - Ex)2
Portanto:
=\left&space;[\int_a^bx^2f(x)dx&space;\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2=\left&space;[\int_a^bx^2\left&space;(\fracb-a2&space;\right&space;)&space;dx\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2)
=\frac(b-a)^212)
D (x) = √ V (x)
=\sqrt\frac(b-a)^212)
Mediana, moda, simetria e curtose
Pode -se verificar facilmente que a mediana, que é o valor central da distribuição uniforme, é igual à média e, como não há valor que seja repetido mais do que outros, uma vez que todos são igualmente prováveis no intervalo [a, b ], a moda não existe.
Quanto à simetria, a distribuição uniforme é simétrica e a curtose, que é o grau em que os valores ao redor do centro estão concentrados é -6/5.
Pode atendê -lo: quais são os 7 elementos da circunferência?Exemplos
Várias situações podem ser modeladas através da distribuição contínua e, assim, prevêem seu comportamento. aqui estão alguns exemplos:
Exemplo 1
Uma empresa que fornece serviço elétrico fornece níveis de tensão distribuídos uniformemente, entre 123.0 V e 125.0 v. Isso significa que no tiro doméstico é possível obter qualquer valor de tensão que pertence a esse intervalo.
Então, como visto acima, o gráfico da função de densidade é o retângulo vermelho:
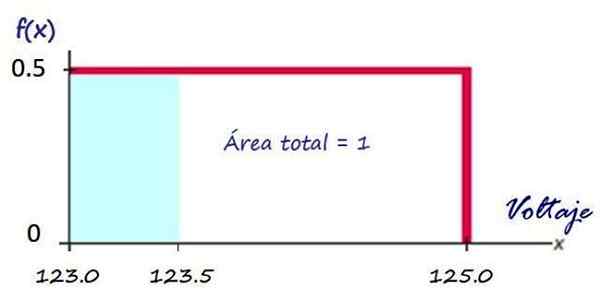Figura 3. Função de densidade para a tensão entregue por uma empresa de eletricidade. Fonte: f. Zapata. Cálculo da probabilidade de ter uma tensão dentro do intervalo especificado é muito fácil, por exemplo, qual é a probabilidade de a empresa enviar uma tensão menor que 123.5 v?
Essa probabilidade é equivalente à área do retângulo sombreado em azul:
P (x<123.5) = (123.5 −123.0)x 0.5 = 0.25
E qual é a probabilidade de a tensão entregue ser maior que 124.0 v?
Como a área total é igual a 1, a probabilidade procurada é:
P (x> 124.0 V) = 1 - (1 × 0.5) = 0.5
Faz sentido, desde 124.0 é precisamente o valor no centro do intervalo.
Exemplo 2
Uma certa variável aleatória x tem uma distribuição uniforme no intervalo [0,100]. Determinar:
a) a probabilidade de que o valor de x seja menor que 22.
b) a probabilidade de X levar valores entre 20 e 35.
c) o valor esperado, a variação e o desvio padrão desta distribuição.
Responda para
É determinado semelhante ao exemplo anterior, mas primeiro devemos determinar a altura do retângulo, lembrando que a área total deve ser igual a 1:
Área = 100 × altura = 1
Portanto, o retângulo tem uma altura igual a 1/100 = 0.01
Pode servir a você: Decágono: regular, irregular, propriedades, exemplosP (x<22) = 22×0.01 = 0.22
Resposta b
A probabilidade solicitada é equivalente à área do retângulo cuja largura é (35 - 20) e cuja altura é 0.01:
P (22 Se você preferir ir diretamente para a função de distribuição acima, basta substituir os valores em: P (20≤x≤35) = f (35) -f (20) Com f (x) dado por: F (x) = (x-a) / (b-a) Os valores a serem introduzidos são: A = 0 B = 100 F (35) = (35-0) / (100-0) = 0.35 F (20) = (20-0) / (100-0) = 0.vinte P (20≤x≤35) = 0.35-0.20 = 0.quinze O valor esperado é: E (x) = (a+b)/2 = (100+0)/2 = 50 A variação é: V (x) = (b-a)2/12 = (100-0)2/12 = 833.33 E o desvio padrão é: D (x) = √833.33 = 28.87 Essa distribuição é útil quando os processos de simulação estatística são realizados ou ao trabalhar em eventos cuja frequência de aparência é regular. Algumas linguagens de programação geram números aleatórios entre 0 e 1 e, como pode ser visto nos exemplos anteriores, a distribuição de probabilidades seguidas é uniforme. Nesse caso, o intervalo a considerar é [0,1]. Se você tem um experimento no qual os eventos têm regularidade, conforme explicado acima, você pode, em princípio, atribuir a cada um da mesma probabilidade de ocorrência. Nesse caso, o modelo probabilístico de distribuição uniforme fornece informações para a análise. A distribuição uniforme também é usada no arredondamento das diferenças entre os valores observados e os valores reais de uma variável, assumindo uma distribuição uniforme do erro em um determinado intervalo, de acordo com o arredondamento, geralmente de -0,5 a +0.5.Resposta c
Formulários
Números aleatórios
Amostragem de distribuição arbitrária
Arredondamento de erro
Referências