Cultura e sociedade em geral

Distribuição exponencial

1002
111
Ernesto Bruen

Explicamos o que é distribuição exponencial, suas características, fórmulas, exemplos e exercícios resolvidos

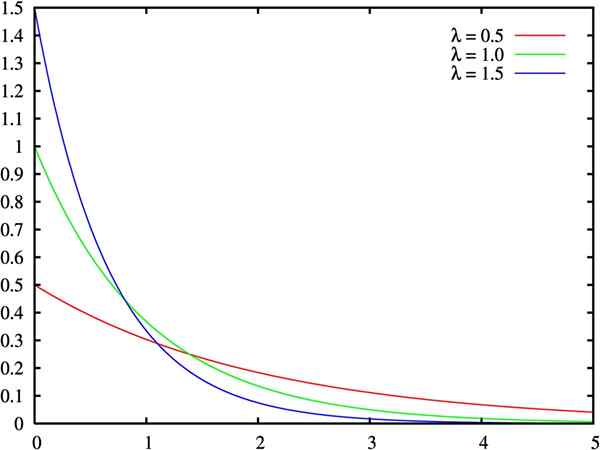
Gráfico da função de densidade da distribuição exponencial, para três valores do parâmetro lambda. Fonte: Wikimedia Commons.

O que é distribuição exponencial?

O distribuição exponencial É um modelo probabilístico para variáveis aleatórias contínuas. Isso significa que, através dele, você pode saber a probabilidade de ocorrência de um certo valor da variável, por isso é uma distribuição de probabilidade.

Para obter a distribuição, começa de um Função de densidade, que tem uma forma exponencial do parâmetro λ> 0:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ texto Sim x \ leq 0 \ End casos$

A função de densidade como tal não permite calcular a probabilidade, mas uma vez estabelecido f (x), a função de distribuição F (x), pela qual as probabilidades são obtidas, é obtida pela integração de f (x). Por exemplo, a probabilidade P de que a variável aleatória leva valores entre 0 e x é:

$F(x)=P[x\leq x]=\int_0^xf(x)dx$

Realizar a integração, que é muito simples, uma vez que a integral de um exponencial é a mesma exponencial, exceto as constantes que acompanham o argumento, é obtido:

$F(x)=\int_0^x\lambda e^-\lambda xdx=\lambda \left (-\frac1\lambda \right )\left [ e^-\lambda x \right ]_0^x=-\left (e^-\lambda x-e^0 \right )=1-e^-\lambda x$

A distribuição exponencial é amplamente usada para determinar a probabilidade de um evento após um certo tempo de espera, como o tempo que ocorre no surgimento de um hospital antes que um paciente chegue.

Freqüentemente, os eventos se referem à falha ou quebra de tipos elétricos, eletrônicos e outros. Nesse caso, a distribuição exponencial ajuda a estimar o tempo que leva para um componente falhar e também o tempo entre os reparos. Isso é conhecido como teoria de confiabilidade.

Características da distribuição exponencial

Algumas das características mais destacadas da função de densidade f (x) da distribuição exponencial são as seguintes:

f (x) é positivo.
A área sob a curva y = f (x) = λe^−λ^x É sempre igual a 1, porque a soma das probabilidades de ocorrência de todos os valores da variável deve ser 1. Esta é uma condição que as funções de densidade cumprem. Esta área é calculada através da integral:

Pode atendê -lo: Anuma

$\int_-\infty ^\infty f(x)dx=\int_-\infty ^\infty \lambda e^-\lambda xdx=1$

Falta de memória de distribuição exponencial

A característica mais destacada da distribuição exponencial é sua falta de memória. Por exemplo, suponha que o tempo decorrido esteja sendo modelando com essa distribuição até que a falha de um elemento ocorra.

Bem, a falta de memória refere -se a saber que o elemento funcionou para um tempo de sobrevivência "S", não modifica a probabilidade de que o elemento continue a subir até um certo período de tempo adicional "t".

Ou seja, a probabilidade de o elemento falhar daqui para um certo tempo (1 minuto, 1 hora, por exemplo) não depende de ter funcionado bem até agora.

Matematicamente, é calculado por definição de probabilidade de eventos independentes:

$P[x\geq s+t/x\geq s]=\fracP[x\geq s+t]P[x\geq s]=\frac1-F(s+t)1-F(s)=\frac1- [1-e^-\lambda (s+t) ]1- [1-e^-\lambda s ]= \beginmatrix \\ \endmatrix$

$=e^-\lambda t$

Portanto, a probabilidade não depende de s ou tempo de sobrevivência.

Fórmulas

1.- A função de densidade da distribuição exponencial é:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ texto Sim x \ leq 0 \ End casos$

Onde λ é o parâmetro de distribuição.

2.- Como descrito acima, a distribuição das probabilidades é indicada como f (x) e as diferentes probabilidades são obtidas pela integração da função de densidade:

$F(x)=\begincases 0 & \text si x\leq 0 \\ 1-e^-\lambda x& \text si x>0 \ End casos$

3.- Do exposto, segue -se que a probabilidade de a variável levar valores menores ou iguais a "x" é p [x≤x] = 1 −e^−λ^x.

4.- A área sob a curva y = f (x), incluída entre A e B, permite calcular a probabilidade de a variável estar no intervalo [a, b]. Esta área é:

P [a ≤ x ≤ b] = f (b) - f (a)

5.- O valor de p [x ≥ a] é 1 - f (a) = 1 - (1 - e^−λ^x) = e^−λ^x

Valor esperado da distribuição exponencial

A esperança ou o valor esperado e (x) da distribuição exponencial é o valor que deve ocorrer com mais frequência. É calculado a partir da integral:

Pode atendê -lo: técnicas de registro de informações

$E(x)=\int_0^\infty xf(x)dx$ Que é facilmente resolvido pelo método de integração por peças. O resultado é:

E (x) = 1/λ

Variação da distribuição exponencial

Para o cálculo da variação, a integral deve ser determinada:

$Var(x)=\int_0^\infty x^2f(x)dx$

Que também é resolvido com o método de integração por peças, para obter:

Var (x) = 1/λ²

Uma particularidade da distribuição exponencial é que o desvio padrão s (x), definido como a raiz quadrada da variação é:

S (x) = √var (x) = √ (1/λ²) = 1/λ

Isto é, o desvio padrão é igual à esperança de distribuição.

Exemplos de distribuição exponencial

Datação de amostras de carbono 14

A distribuição exponencial é usada para determinar o tempo necessário para desintegrar uma partícula radioativa. Esses tempos são usados para namorar amostras fósseis por radiocarbono.

Tempo leva para verificar o e -mail

Você pode modelar o tempo que os usuários levam para revisar seu email, assim que a notificação for recebida, por meio de uma distribuição exponencial. Suponha que o parâmetro de distribuição seja λ = 0.2, então, a probabilidade de uma pessoa levar menos de 1 minuto para revisar seu e -mail é:

$P[x\leq 1]=\int_0^1f(x)dx=\int_0^10.2e^-0.2xdx$

Esta integral foi resolvida no início, resta apenas para substituir os valores numéricos na solução e calcular o resultado final:

P [x ≤ 1] = 1 --e^-^0.2^×¹ = 1− e^-^0.2 = 1− 0.819 = 0.181

Também pode ser substituído diretamente na função f (x) dada acima, para obter f (1).

Exercícios

Exercício 1

Encontre a probabilidade de uma pessoa mais tarde uma hora revisando seu email, se a distribuição de probabilidade for exponencial, com o parâmetro λ = 0.2.

Solução

P [x ≥ 60] deve ser calculado, pois 1 hora é equivalente a 60 minutos e a probabilidade de que a pessoa tardio de 60 minutos ou mais para verificar se o e -mail é solicitada. A probabilidade é calculada com a mesma integral apresentada no início, apenas alterando os limites de integração:

Pode atendê -lo: Rapa Nui: História, Características, Cultura, Tradições

$P[x\geq 60]=\int_60^\infty 0.2e^-0.2xdx=-\left ( -e^-0.2\times 60 \right )=0.000006144$

O valor obtido é pequeno, por isso é muito improvável que uma pessoa leve mais de uma hora para revisar seu e -mail.

Exercício 2

As lâmpadas elétricas geralmente têm uma duração finita, exceto a famosa lâmpada do quartel de bombeiros em Livermore, Califórnia, que nunca falhou desde a primeira vez, em 1901.

Suponha que a duração de uma lâmpada atual siga uma distribuição exponencial, com um valor esperado de 8 meses. Calcular:

a) Qual é a probabilidade de a lâmpada durar entre 5 e 14 meses?

b) a probabilidade de a lâmpada durar mais de 25 meses, sabendo que tem mais de 11 meses em operação.

Solução para

A primeira coisa é encontrar o valor de λ, através do valor esperado da distribuição e (x) = 8 meses. De acordo com o que foi dito na seção anterior, o valor esperado é o inverso do parâmetro λ, portanto:

E (x) = 1 /λ → λ = 1 /e (x) = 1/8 = 0.125

Em seguida, a probabilidade solicitada é calculada, por meio da integral dada no início, mas alterando convenientemente os limites de integração:

Em seguida, é substituído na função f (x) dada na seção anterior, como segue:

P [5 ≤ x ≤ 14] = f (14) - f (5) = [1 - e^{-(0.125 × 14)}] - [1 - e^{-(0.125 × 5)}] = 0.36

Solução b

Para responder a essa questão, a propriedade da falta de memória será usada, enunciada acima. Como se sabe que já durou mais de 11 meses, então:

S = 11 meses

O tempo adicional para durar 25 meses ou mais é:

T = 14 meses

P [x ≥ s + t│t ≥ s] = p [x ≥ 11 + 14│t ≥ 11] = e^{-0.125 × 14}= 0.174