Diferença de fórmulas, equações, exemplos, exercícios

O Diferença de cubos É uma expressão algébrica binomial da forma para³ - b³, onde os termos A e B podem ser números reais ou expressões algébricas de vários tipos. Um exemplo de diferença de cubos é: 8 - x³, já que 8 podem ser escritos como 2³.

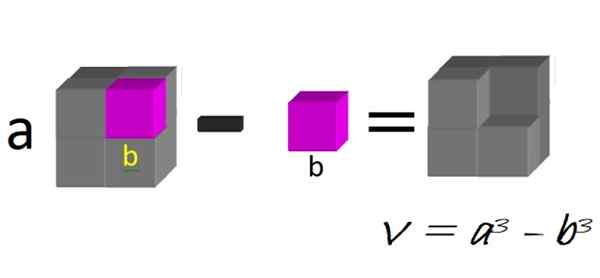
Geometricamente, podemos pensar em um cubo grande, do lado a, para o qual o pequeno bubo do lado B é subtraído, conforme ilustrado na Figura 1:

figura 1. Uma diferença de cubos. Fonte: f. Zapata.

O volume da figura resultante é precisamente uma diferença nos cubos:

V = a³ - b³

Para encontrar uma expressão alternativa, observa -se que essa figura pode ser dividida em três prismas, como mostrado abaixo:

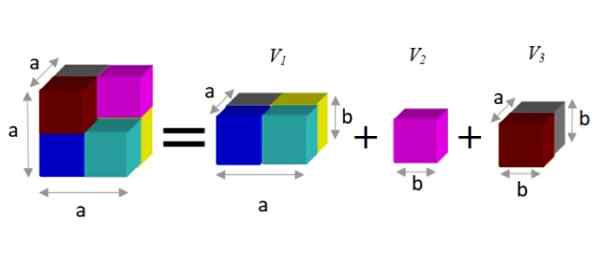Figura 2. A diferença nos cubos (à esquerda da igualdade) é igual à soma dos volumes parciais (à direita). Fonte: f. Zapata.

Um prisma tem um volume dado pelo produto de suas três dimensões: largura x alta x profundidade. Dessa forma, o volume resultante é:

V = a³ - b³ = a².b + b³ + para.b²

O fator b É comum ao certo. Além disso, na figura mostrada acima, é cumprida em particular que:

b = (a/2) ⇒ a = b + b

Portanto, pode -se dizer que: b = a - b. Desta forma:

para³ - b³ = B (A² + b² +para.b) = (a-b) (a² + para.b + b²)

Essa maneira de expressar a diferença nos cubos será muito útil em muitas aplicações e teria sido obtida da mesma maneira, embora o lado do cubo que falta no canto fosse diferente de B = a/2.

Observe que o segundo parênteseParece muito para o produto notável do quadrado da soma, mas o termo cruzado não é multiplicado por 2. O leitor pode desenvolver o lado certo para verificar se é efetivamente obtido para³ - b³.

[TOC]

Pode atendê -lo: binomial quadrado

Exemplos

Existem várias diferenças de cubos:

1 - m⁶

para⁶b³ - 8z¹²e⁶

(1/125).x⁶ - 27.e⁹

Vamos analisar cada um deles. No primeiro exemplo, o 1 pode ser escrito como 1 = 1³ e o termo m⁶ Permanece: (M²)³. Ambos os termos são cubos perfeitos, portanto, sua diferença é:

1 -M⁶ = 1³ - (m²)³

No segundo exemplo, os termos são reescritos:

para⁶b³ = (a²b)³

8z¹²e⁶ = 2³ (Z⁴)³ (e²)³ = (2z⁴e²)³

A diferença desses cubos é: (a²b)³ - (2z⁴e²)³.

Finalmente, a fração (1/125) é (1/5³), x⁶ = (x²)³, 27 = 3³ e e⁹ = (e³)³. Substituindo tudo isso na expressão original, é obtido:

(1/125).x⁶  - 27y⁹ = [(1/5) (x²)]³ - (3y³)³

Fatoração de uma diferença de cubos

Fato da diferença em cubos simplifica muitas operações algébricas. Para fazer isso, basta usar a fórmula deduzida anteriormente:

Figura 3. Fator da diferença nos cubos e expressão de um quociente notável. Fonte: f. Zapata.

Agora, o procedimento para aplicar esta fórmula consiste em três etapas:

- Primeiro, a raiz cúbica de cada um dos termos da diferença é obtida.

- Então o binomial e o trinômio que aparecem no lado direito da fórmula são construídos.

- Finalmente, o binomial e o trinomial são substituídos para obter a fatorização final.

Ilustraremos o uso dessas etapas com cada um dos exemplos de diferença de cubos propostos acima e, assim, obterá seu equivalente fatorizado.

Exemplo 1

Expressão da Factiva 1 -M⁶   Seguindo as etapas descritas. Começamos reescrevendo a expressão como 1 -m⁶ = 1³ - (m²)³ Para extrair as respectivas raízes cúbicas de cada termo:

Então o binomial e o trinomial são construídos:

Pode servir a você: teoria da fila: história, modelo, para que serve e exemplos para

A = 1

b = m²

Então:

A - B = 1 - M²

 (para² +para.b + b²) = 1² + 1.m² + (m²)² = 1 + m² + m⁴

 Finalmente é substituído na fórmula A³ - b³ = (a-b) (a² +para.b + b²):

1 -M⁶ = (1 - m²) (1 + m² + m⁴)

Exemplo 2

Fatore:

para⁶b³ -8z¹²e⁶ = (a²b)³ - (2z⁴e²)³

Como esses são cubos perfeitos, as raízes cúbicas são imediatas: um²B e 2z⁴e², A partir daí, segue -se:

- Binomial: a²B - 2z⁴e²

- Trinomial: (a²b)² + para²b. 2z⁴e² + (para²B +2z⁴e²)²

 E agora a fatoração desejada é construída:

para⁶b³ -8z¹²e⁶ = (a²B - 2z⁴e²). [(para²b)² + para²b. 2z⁴e² + (para²B + 2z⁴e²)²] =

= (a²B - 2z⁴e²). [para⁴b² + 2º²b.z⁴e² + (para²B + 2z⁴e²)²]

Em princípio, a fatorização está pronta, mas geralmente é necessário simplificar cada termo. Em seguida, o produto notável é desenvolvido a partir de uma soma - que aparece no final e depois adiciona termos semelhantes. Lembrando que o quadrado de uma soma é:

(x + y)² = x² + 2xy + e²

O direito notável à direita se desenvolve dessa maneira:

(para²B + 2z⁴e²)² = a⁴b² + 4º²b.z⁴e² + 4z⁸e⁴

 Substituindo o desenvolvimento obtido na fatoração da diferença nos cubos:

para⁶b³ -8z¹²e⁶ = (a²B - 2z⁴e²). [para⁴b² + 2º²b.z⁴e² + para⁴b² + 4º²b.z⁴e² + 4z⁸e⁴] =

Finalmente, agrupando termos semelhantes e considerando os coeficientes numéricos, que são todos pares, é obtido:

(para²B - 2z⁴e²). [2º⁴b² + 6º²b.z⁴e² + 4z⁸e⁴] = 2 (A²B - 2z⁴e²). [para⁴b² + 3º²b.z⁴e² + 2z⁸e⁴]

Exemplo 3

Facione (1/125).x⁶  - 27y⁹ É muito mais simples que o caso anterior. Primeiro, os equivalentes de A e B são identificados:

A = (1/5) x²

B = 3y³

Então eles são substituídos diretamente na fórmula:

(1/125).x⁶  - 27y⁹ = [(1/5) x² - 3y³]. [(1/25) x⁴ + (3/5) x²e³ + 9y⁶]

Exercício resolvido

A diferença nos cubos, como dissemos, uma variedade de aplicações em álgebra. Vejamos alguns:

Pode atendê -lo: 5 características do avião cartesiano

Exercício 1

Resolva as seguintes equações:

a) x⁵ - 125 x² = 0

b) 64 - 729 x³ = 0

Solução para

Primeiro, a equação é o fator dessa maneira:

x² (x³ - 125) = 0

Como 125 é um cubo perfeito, os parênteses são escritos como uma diferença nos cubos:

x² . (x³ - 5³) = 0

A primeira solução é x = 0, mas encontramos mais se fizermos x³ - 5³ = 0, então:

x³ = 5³ → x = 5

Solução b

O lado esquerdo da equação é reescrito como 64 - 729 x³ = 4³ - (9x)³. Portanto:

4³ - (9x)³ = 0

Como o expoente é o mesmo:

9x = 4 → x = 9/4

Exercício 2

Fatore a expressão:

(x + y)³ - (X - y)³

Solução

Esta expressão é uma diferença nos cubos, se na fórmula da fatoração, notamos que:

A = x+ e

b = x- y

Então o binomial é construído primeiro:

a - b = x+ y - (x-) = 2y

E agora o trinomial:

para² + para.b + b² = (x+ y)² + (x + y) (x-y) + (x-y)²

Produtos notáveis ​​são desenvolvidos:

(x+ y)² = x² + 2xy +e²

(x+y) (x-y) = x²- e²

(x- y)² = x² - 2xy +e²

Então você deve substituir e reduzir termos semelhantes:

para² + para.b + b² = x² + 2xy +e²+ x²- e²+ x² - 2xy +e² = 3x² + e²

A fatoração resulta em:

(x + y)³ - (X - y)³ = 2y. (3x² + e²)

Referências

1. Baldor, a. 1974. Álgebra. Editorial cultural venezuelano.PARA.
2. Fundação CK-12. Soma e diferença de cubos. Recuperado de: CK12.org.
3. Academia Khan. Fator da diferença de cubos. Recuperado de: é.Khanacademy.org.
4. Matemática é divertida avançada. Diferença de dois cubos. Recuperado de: Mathsisfun.com
5. Unam. Fatoração de uma diferença de cubos. Recuperado de: DCB.Fi-c.Unam.mx.