Deslocamento angular

O que é deslocamento angular?

Ele Deslocamento angular É a mudança ou variação na posição angular que um objeto nas experiências de rotação, geralmente medido em radianos ou qualquer outra medida dada para turnos, como notas ou revoluções.

Quando um objeto gira em torno de um eixo fixo, seu deslocamento angular é determinado medindo o ângulo varrido por uma linha que passa por qualquer ponto do corpo que cruze o eixo de rotação, ou seja, uma linha radial.

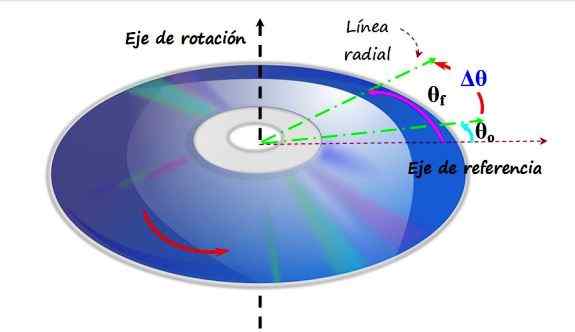Um disco ou CD compacto gira em uma direção anti -histórica em torno de um eixo de rotação vertical. Ao passar do ângulo θo para θf, diz -se que ele experimentou um deslocamento angular. Fonte: f. Zapata.

Na figura superior, há um CD que gira em uma direção anti -hecome, sendo seu eixo de rotação o eixo vertical. Um eixo de referência é colocado no plano do CD, que corresponde ao ângulo 0 radianos ou 0. A linha verde é uma linha radial, que está inicialmente formando um ângulo θ_qualquer Com a referência. Esta é a sua posição inicial.

Mais tarde, a linha verde se move para uma nova posição chamada θ_F, E a experiência experimentada, chamada Δθ é simplesmente:

Δθ = θ_F - θ_qualquer

Qualquer ponto P do CD experimenta o mesmo deslocamento angular em um certo intervalo de tempo, exceto o centro, que é onde o eixo de rotação passa e permanece em repouso.

Fórmulas e equações

Existe um objeto que gira em torno de um eixo fixo ou que sai da tela para o leitor. E dentro dele, há o ponto P, localizado a uma distância r do eixo de rotação e descrevendo as circunferências da Rádio R.

Isso é visto na figura a seguir, que mostra um objeto de corte, visto contrário às agulhas do relógio. O ponto em questão está na posição angular θ, medida no eixo de referência, que neste caso é o eixo horizontal.

Pode atendê -lo: princípio aditivo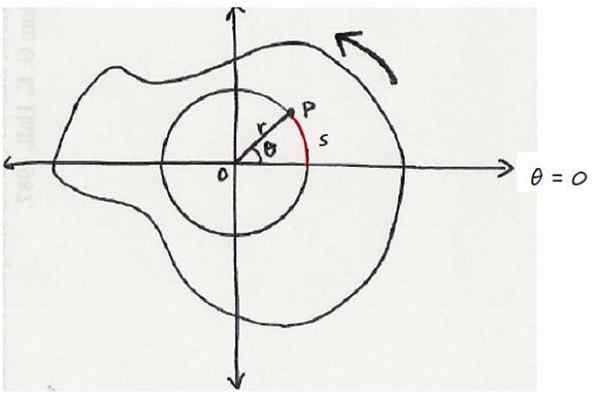Um objeto que gira em um sentido anti -helavói. O eixo de rotação sai perpendicular à tela. Fonte: Wikimedia Commons.

Por convenção, para a rotação em um sentido anticorárico, é atribuído sentido positivo, enquanto a rotação em um cronograma tem um sinal negativo.

Como o ponto P jura o ângulo θ, ele viaja simultaneamente o arco. Como θ é um ângulo central, uma vez que seu vértice ocupa o centro da circunferência, é cumprido que:

Com θ expresso em Radianes.

O deslocamento angular é:

Δθ = θ_final  - θ_inicial

Por exemplo, se P começou com θ_inicial = 0 rad e então está em θ_final = 0.8 rad, seu deslocamento angular é de:

Δθ = 0.8 rad - 0 rad =  0.8 rad

Outros pontos do objeto podem ocupar diferentes posições angulares, mas todos experimentam o mesmo deslocamento angular. No entanto, as partículas mais remotas do centro viajam com distâncias maiores, já que S = r⋅θ.

Ângulos medem

Na rotação, é comum encontrar os ângulos medidos em radianos, mas eles também são encontrados em graus e revoluções ou voltas. Na solução de problemas, é necessário passar dessas unidades para Radianes.

1 A revolução é equivalente a uma curva completa, ou seja, quando uma curva completa quebrada, ela girou 360 º e estes são equivalentes a 2π radianos, pois nesse caso, o ponto visitou um arco igual a 2πr:

Mas simplificando, a equivalência anterior pode ser expressa da seguinte forma:

π radianes = 180º

Como é calculado o deslocamento angular?

O deslocamento angular pode ser calculado de maneira analogada como o deslocamento do movimento é calculado em uma dimensão, seguindo um certo modelo de movimento. Para isso, a velocidade angular média é definida como o deslocamento angular Δθ em um determinado intervalo de tempo Δt:

Onde a velocidade angular média é indicada como ω_m e é dado em radianos em unidades do sistema internacional se.

Pode atendê -lo: como obter o ângulo de um triângulo? (Exemplo)

A velocidade angular instantânea é o limite da velocidade angular média quando Δt → 0:

Isto é, é o primeiro derivado da posição angular em relação ao tempo. Por sua vez, uma aceleração angular pode ser definida, indicada como α, que é equivalente à taxa de derivada ou mudança de velocidade angular em relação ao tempo:

Que também pode ser interpretado como o segundo derivado da posição angular em relação ao tempo.

O importante é que dois modelos de movimento podem ser estabelecidos em analogia com os movimentos retilíneos, pois, embora as rotações sejam realizadas no plano, uma única coordenada angular é suficiente para estabelecer a posição de qualquer ponto do objeto.

Movimento circular uniforme

No movimento circular uniforme, a velocidade angular é constante, ou seja, a velocidade angular média é igual à velocidade angular instantânea. Como a aceleração angular α é igual a 0, você pode escrever a seguinte equação para a posição em função do tempo:

θ = θ_qualquer + ωt

Onde θ_qualquer É a posição inicial do celular.

Movimento circular uniformemente acelerado

Nesse caso, a aceleração angular α é constante e, em analogia com o movimento retilíneo uniformemente variado, as seguintes equações podem ser escritas:

• θ = θ_qualquer + Ω_qualquer T + ½ αT²
• Ω = ω_qualquer + αT 
• Ω² = Ω_qualquer² + 2α ∙ Δθ

Exercício resolvido

Primeiro exercício

Pode -se supor que a terra é um objeto rígido que gira em um eixo fixo e que sua rotação é quase uniforme. No intervalo de tempo Δt = 12 h encontre:

a) o deslocamento angular da terra

b) sua velocidade angular

c) aceleração angular durante esse intervalo de tempo.

Solução para

Sabendo que em 24 horas a Terra dá uma volta completa em torno de seu eixo, em 12 horas você virou metade de uma volta, isto é, π radianes. Se for considerado que parte de θ_inicial = 0 rad, então seu deslocamento angular é:

Pode servir a você: Princípio multiplicativo: Técnicas e exemplos de contagem

Δθ = π radianos

Solução b

Como a rotação é uniforme, a velocidade angular é o quociente entre deslocamento angular e tempo, além disso, 1 hora = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 rad/s.

Solução c

A aceleração angular é nula, pois a rotação da terra é uniforme.

Segundo exercício

Juan percorreu uma distância de 35 metros em uma pista de atletismo circular cujo raio é igual a 7 metros. Calcule o deslocamento angular que Juan fez.

Solução

Como a distância do arco viajada e o raio da circunferência são conhecidos, a segunda fórmula pode ser aplicada para conhecer o deslocamento angular feito por Juan. Usando a fórmula descrita acima, você precisa θ = 35/7 = 5 radianos.

Terceiro exercício

Se Mario precisa em seu veículo, metade de uma pista de corrida circular, qual é o deslocamento angular que Mario fez?

Solução

Neste exercício, a primeira fórmula será aplicada. Como se sabe que Mario viajou metade da pista, pode -se supor que ele começou a corrida em ângulo 0 ° e quando atingiu metade da circunferência, viajou 180 °. Portanto, a resposta é 180 ° -0 ° = 180 ° = π radianos.

Quarto exercício

Maria tem uma piscina circular. Seu cachorro corre pela piscina viajando a uma distância de 18 metros. Se o raio da piscina for de 3 metros, qual é o deslocamento angular feito pelo animal de estimação de Maria?

Solução

Como a piscina é circular e o raio é conhecido, você pode usar a segunda fórmula.

Sabe -se que o raio é igual a 3 metros e a distância percorrida pelo animal é igual a 18 metros. Portanto, o deslocamento angular realizado é igual a θ = 18/3 = 6 radianos.

Referências

1. Katz, d. 2013. Física para cientistas e engenheiros. Fundações e conexões. Cengage Learning.
2. Rex, a. 2011. Fundamentos da Física. Pearson.
3. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1. Pearson.
4. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.
5. Tipler, p. (2006). Física para Ciência e Tecnologia. 5ª ed. Volume 1. Editorial revertido.