Desigualdade do triângulo de demonstração, exemplos, exercícios resolvidos

Se denomina Desigualdade do triângulo à propriedade que atende a dois números reais que consistem no valor absoluto de sua soma é sempre menor ou igual à soma de seus valores absolutos. Esta propriedade também é conhecida como desigualdade de Minkowski ou desigualdade triangular.

Essa propriedade dos números é chamada de desigualdade triangular, porque nos triângulos acontece que o comprimento de um lado é sempre menor ou igual à soma dos outros dois, mesmo que essa desigualdade nem sempre se aplique no campo de triângulos.

figura 1. O valor absoluto da soma de dois números é sempre menor ou igual à soma de seus valores absolutos. (Preparado por r. Pérez)

Existem várias demonstrações de desigualdade triangular em números reais, mas neste caso escolheremos um baseado nas propriedades do valor absoluto e no binomial quadrado.

Teorema: Para todos os pares de números para e b Pertencente a números reais, ele tem que:

| A + B | ≤ | a | + | b |

[TOC]

Demonstração

Começamos considerando o primeiro membro da desigualdade, que será reduzido:

| A + b |^2 = (a + b)^2 = a^2 + 2 a b + b^2 (ec. 1)

Na etapa anterior, a propriedade foi usada para que qualquer número alto até o quadrado seja igual ao valor absoluto do referido número alto ao quadrado, ou seja:: | x |^2 = x^2. O desenvolvimento do binomial quadrado também foi usado.

Todo o número x É menor ou igual ao seu valor absoluto. Se o número for positivo, vale a pena igual, mas se o número for negativo, sempre será menor que um número positivo. Nesse caso, seu próprio valor absoluto, ou seja, pode ser afirmado que x ≤ | x |.

Pode atendê -lo: programação não linear: métodos e exercícios

O produto (a b) É um número, portanto, é aplicado que (a b) ≤ | a b |. Quando esta propriedade é aplicada a (CE. 1) Temos:

| A + b |^2 = a^2 + 2 (a b) + b^2 ≤ a^2 + 2 | a b | + B^2 (EC. 2)

Tendo em conta que | A b | = | A || b | LA (EC. 2) Pode ser escrito da seguinte maneira:

 | A + b |^2 ≤ a^2 + 2 | A || b | + B^2 (EC. 3)

Mas, como dissemos antes, o quadrado de um número é igual ao valor absoluto do número alto ao quadrado, a Equação 3 pode ser reescrita da seguinte maneira:

 | A + b |^2 ≤ | a |^2 + 2 | a | | b | + | B |^2 (EC. 4)

No segundo membro da desigualdade, um produto notável é reconhecido, que quando aplicado leva a:

 | A + b |^2 ≤ (| a | + | b |)^2 (ec. 5)

Na expressão anterior, deve -se notar que os valores a serem levantados em ambos os membros da desigualdade também são positivos de que também deve ser cumprido que:

 | A + B | ≤ (| a |+ | B |) (EC. 6)

A expressão anterior é exatamente o que você queria demonstrar.

Exemplos

Em seguida, verificaremos a desigualdade triangular com vários exemplos.

Exemplo 1

O valor é tomado a = 2 e o valor b = 5, ou seja, números positivos e verificamos se a desigualdade é ou não atendida.

 | 2 + 5 | ≤ | 2 |+ | 5 |

 | 7 | ≤ | 2 |+ | 5 |

7 ≤ 2+ 5

A igualdade é verificada, portanto, o teorema da desigualdade do triângulo foi cumprido.

Exemplo 2

Os seguintes valores são escolhidos a = 2 e b = -5, ou seja, um número positivo e o outro negativo, verificamos se a desigualdade é ou não atendida.

Pode atendê -lo: trinomial

 | 2 - 5 | ≤ | 2 |+ | -5 |

 | -3 | ≤ | 2 |+ | -5 |

 3 ≤ 2 + 5

A desigualdade é cumprida, portanto, o teorema da desigualdade triangular foi verificado.

Exemplo 3

O valor é tomado a = -2 e o valor b = 5, ou seja, um número negativo e o outro positivo, verificamos se a desigualdade é ou não atendida.

 | -2 + 5 | ≤ | -2 |+ | 5 |

 | 3 | ≤ | -2 |+ | 5 |

 3 ≤ 2 + 5

A desigualdade é verificada, portanto o teorema foi cumprido.

Exemplo 4

Os seguintes valores a = -2 e b = -5 são escolhidos, ou seja, números negativos e verificamos se a desigualdade é ou não atendida.

 | -2 - 5 | ≤ | -2 |+ | -5 |

 | -7 | ≤ | -2 |+ | -5 |

 7 ≤ 2+ 5

A igualdade é verificada, portanto, o teorema da desigualdade de Minkowsk foi cumprido.

Exemplo 5

O valor é tomado a = 0 e o valor b = 5, ou seja, um número zero e o outro positivo, então verificamos se a desigualdade é ou não atendida.

 | 0 + 5 | ≤ | 0 |+ | 5 |

 | 5 | ≤ | 0 |+ | 5 |

 5 ≤ 0+ 5

A igualdade é cumprida, portanto, o teorema da desigualdade do triângulo foi verificado.

Exemplo 6

O valor é tomado a = 0 e o valor b = -7, ou seja, um número zero e o outro positivo, então verificamos se a desigualdade é ou não atendida.

 | 0 - 7 | ≤ | 0 |+ | -7 |

 | -7 | ≤ | 0 |+ | -7 |

 7 ≤ 0+ 7

A igualdade é verificada, portanto, o teorema da desigualdade triangular foi cumprido.

Exercícios resolvidos

Nos exercícios seguintes, representa geometricamente a desigualdade do triângulo ou desigualdade de Minkowski para os números A e B.

Pode atendê -lo: Papomudas

O número A será representado como um segmento no eixo x, sua origem ou coincide com o zero do eixo x e a outra extremidade do segmento (no ponto P) estará na direção positiva (à direita) do x eixo se A> 0, mas para < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

Da mesma forma, o número B será representado como um segmento cuja origem está no ponto P. O outro lado, ou seja, o ponto que estará à direita de P se B for positivo (b> 0) e o ponto q será | B | unidades à esquerda de P se B<0.

Exercício 1

Representar graficamente a desigualdade do triângulo para a = 5 e b = 3 | A + B | ≤ | a | + | b |, ser C = A + B. 

Solução 1: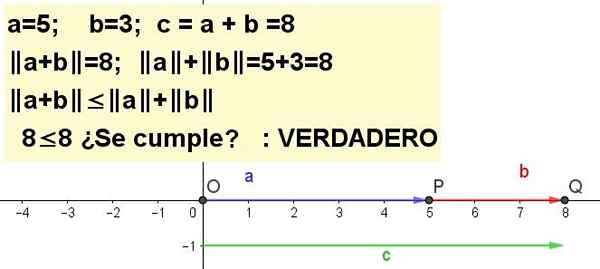

Exercício 2

Faça um gráfico de desigualdade triangular para A = 5 e B = -3. 

| A + B | ≤ | a | + | b |, ser C = A + B.

Solução 2:

Exercício 3

Graça a desigualdade do triângulo para A = -5 e B = 3.

| A + B | ≤ | a | + | b |, ser C = A + B. 

Solução 3: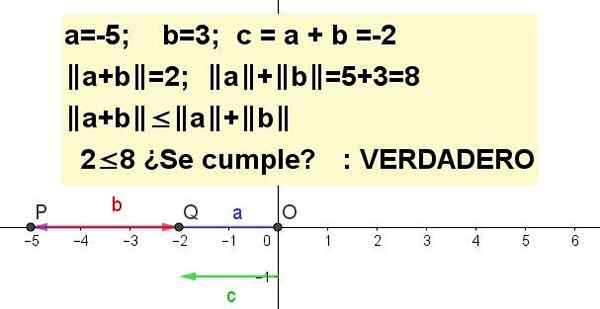

Exercício 4

Graça a desigualdade triangular para A = -5 e B = -3.

| A + B | ≤ | a | + | b |, ser C = A + B.

Solução 4: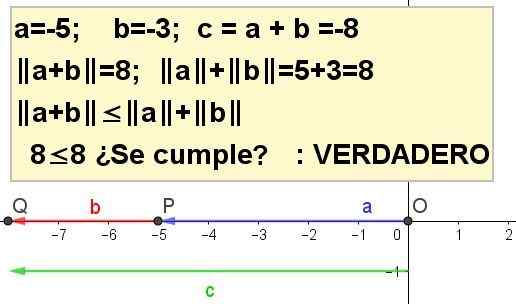

Referências

1. E. Whitesitt. (1980).Álgebra booleana e suas aplicações . Empresa editorial continental C. PARA.
2. Mícheal ou 'Searcoid.(2003) Elementos da análise abstrata ... Departamento de Matemática. University College Dublin, Beldfield, Dublind.
3. J. Van Wyk. (2006) Matemática e Engenharia em Ciência da Computação. Instituto de Ciências e Tecnologia de Computador. Bureau Nacional de Padrões. Washington, d. C. 20234
4. Eric Lehman. Matemática para Ciência da Computação.  Google Inc.
5. F Thomson Leighton (1980). Cálculo. Departamento de Matemática e Ciência da Computação e Laboratório de AI, Instituto de Tecnologia de Massachussetts.
6. Academia Khan. Teorema da desigualdade do triângulo. Recuperado de: Khanacademy.org
7. Wikipedia. Desigualdade triangular. Recuperado de: é. Wikipedia.com