Derivados sucessivos

O que são derivados sucessivos?

As derivados sucessivos Eles são aqueles derivados de uma função após a segunda derivada. O processo para calcular derivados sucessivos é o seguinte: existe uma função f, que podemos derivar e obter a função derivada f '. Para esta derivada de F, podemos derivá -lo novamente, obtendo (f ')'.

Esta nova função é chamada de segunda derivada; Todos os derivados calculados a partir do segundo são sucessivos; Estes, também chamados de uma ordem superior, têm grandes aplicações, como fornecer informações sobre o golpe do gráfico de uma função, o teste da segunda derivada para fins relativos e a determinação da série infinita.

Definição

Usando a notação de Leibniz, temos que o derivado de uma função "y" em relação a "x" é dy/dx. Para expressar ao segundo derivado de "Y" usando a notação de Leibniz, escrevemos o seguinte:

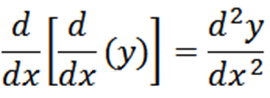
Em geral, podemos expressar derivados sucessivos da seguinte forma com a notação de Leibniz, onde n representa a ordem do derivado.

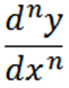
Outras notações usadas são as seguintes:

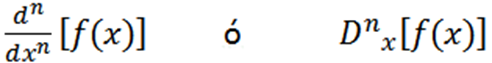
Alguns exemplos em que podemos ver as diferentes notações são:

Exemplo 1

Obtenha todos os derivados da função f definida por:

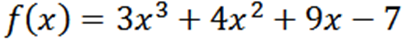
Usando as técnicas usuais de referência, temos que o F é:

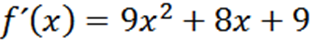
Repetindo o processo, podemos obter o segundo derivado, o terceiro derivado e assim por diante.

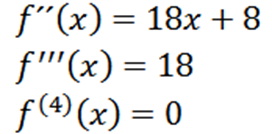
Observe que o quarto derivado é zero e o derivado zero é zero, então temos que::

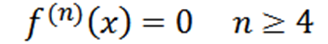
Exemplo 2

Calcule o quarto derivado da seguinte função:

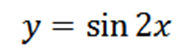
Derivando a função dada que temos como resultado:

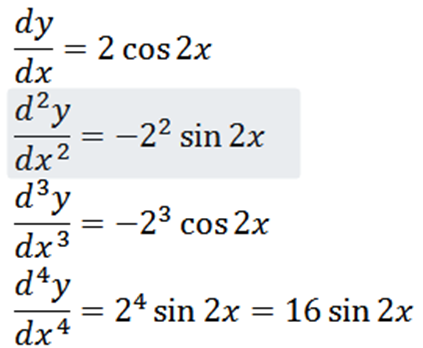
Velocidade e aceleração

Uma das motivações que levaram à descoberta da derivada foi a busca pela definição de velocidade instantânea. A definição formal é a seguinte:

Pode atendê -lo: números primos: características, exemplos, exercícios

Seja y = f (t) uma função cujo gráfico descreve a trajetória de uma partícula em um instante t, Então sua velocidade em um instante T é dada por:

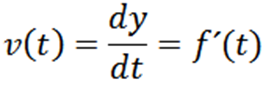
Depois que a velocidade de uma partícula é obtida, podemos calcular a aceleração instantânea, que é definida da seguinte forma:

A aceleração instantânea de uma partícula cuja trajetória é dada por y = f (t) é:

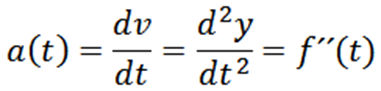
Exemplo 1

Uma partícula se move em uma linha de acordo com a função de posição:

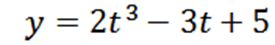
Onde "y" é medido em metros e "t" em segundos.

• Em que momento sua velocidade é 0?
• Em que momento sua aceleração é 0?

Derivando a função de posição "Y", temos que sua velocidade e aceleração são dadas respectivamente por:

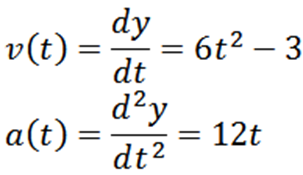
Para responder à primeira pergunta, basta determinar quando a função V v é zero; isto é:

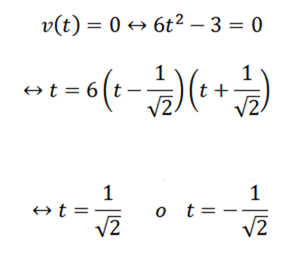
Continuamos com a próxima pergunta análoga:

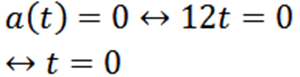
Exemplo 2

Uma partícula se move em uma linha de acordo com a seguinte equação de movimento:

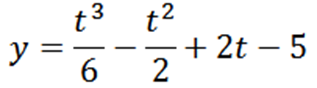
Determinar "t, y" e "v" quando a = 0.

Sabendo que velocidade e aceleração são dadas por

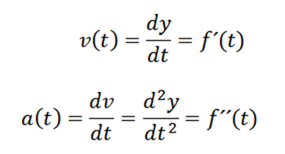
Passamos a derivar e obter:

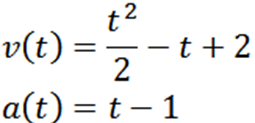
Fazendo A = 0, temos:

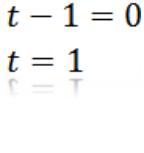
Onde podemos deduzir que o valor de t para que a seja igual a zero é t = 1.

Em seguida, avaliando em t = 1 a posição e função da função, temos que:

Formulários

Derivação MPLÍCITA

Derivados sucessivos também podem ser obtidos por derivação implícita.

Exemplo

Dado a seguinte elipse, encontre "y":

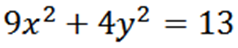
Derivado implicitamente em relação a x, temos:

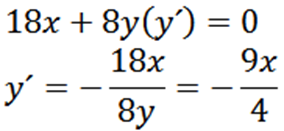
Em seguida, reviver implicitamente em relação a X, nos dá:

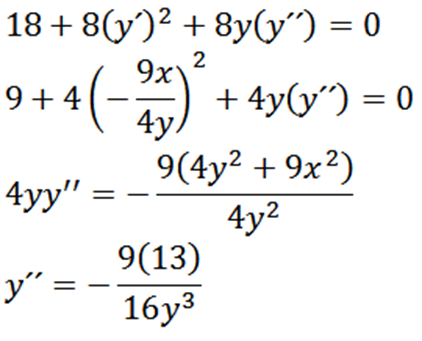
Finalmente, temos:

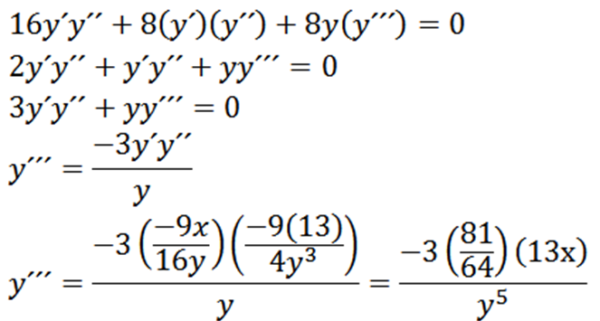
Extremos relativos

Outro uso que podemos dar aos derivados de segunda ordem está no cálculo das extremidades relativas de uma função.

Pode atendê -lo: quantos eixos de simetria um círculo tem?

Os critérios da primeira derivada para extremos locais nos dizem que, se tivermos uma função F contínua em um intervalo (a, b) e há um c que pertence ao referido intervalo, de modo que seja anulado em c (ou seja, que C é um ponto crítico), um desses três casos pode ocorrer:

• Se f '(x)> 0 para qualquer X pertencente a (a, c) e f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
• Se f '(x) 0 para x pertencer a (c, b), então f (c) é um mínimo local.
• Se f '(x) tiver a mesma fatura (a, c) e em (c, b), isso implica que f (c) não é um fim local.

Usando os critérios da segunda derivada, podemos saber se um número crítico de uma função é um mínimo máximo ou local, sem ter que fazer o que é o sinal da função nos intervalos mencionados acima mencionados.

O critério da segunda deriva nos diz que se f '(c) = 0 e que f "(x) for contínuo em (a, b), isso acontece se f" (c)> 0 então f (c) é a Mínimo local e se f "(c) < 0 entonces f(c) es un máximo local.

Se f "(c) = 0, não podemos concluir nada.

Exemplo

Dada a função f (x) = x⁴ + (4/3) x³ - 4x², Encontre o parente máximo e mínimo de f aplicando os critérios da segunda derivada.

Primeiro, calculamos f '(x) e f "(x) e temos:

f '(x) = 4x³ + 4x² - 8x

f "(x) = 12x² + 8x - 8

Agora, f '(x) = 0 sim, e somente se 4x (x + 2) (x - 1) = 0, e isso ocorre quando x = 0, x = 1 ou x = - 2.

Para determinar se os números críticos obtidos são extremos relativos apenas avaliados em f "e, assim, observe seu sinal.

Pode servir você: heptagon

f "(0) = - 8, então f (0) é um máximo local.

F "(1) = 12, então F (1) é um mínimo local.

F "(- 2) = 24, então F (- 2) é um mínimo local.

Série Taylor

Ser f uma função definida da seguinte forma:

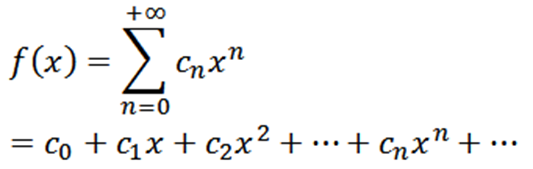
Esta função tem um raio de convergência r> 0 e derivou de todos os pedidos em (-r, r). Derivados sucessivos de F nos dão:

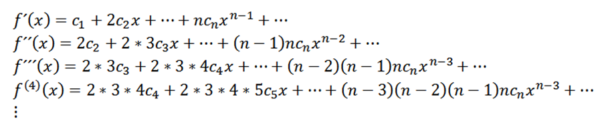
Tomando x = 0, podemos obter os valores de C_n Dependendo de seus derivados da seguinte forma:

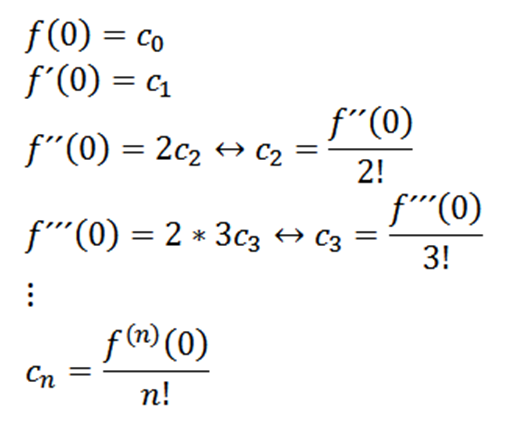
Se tomarmos n = 0 como a função f (ou seja, f^0 = f), podemos reescrever a função da seguinte forma:

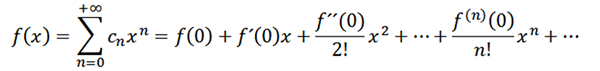
Agora vamos considerar a função como uma série de poderes em x = a:

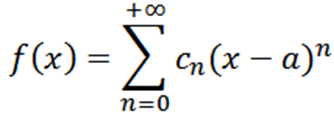
Se executarmos uma análise análoga à anterior, teríamos que escrever a função f como:

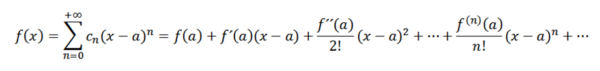
Essas séries são conhecidas como Taylor F em uma série. Quando A = 0 temos o caso específico chamado Maclaurin Series. Esse tipo de série é de grande importância matemática, especialmente na análise numérica, pois, graças a isso, podemos definir funções em computadores como e^x , sin (x) e cos (x).

Exemplo

Obtenha a série Maclaurin para E^x.

Observe que se f (x) = e^x, então f^(N)(x) = e^x e f^(N)(0) = 1, então sua série Maclaurin é: