Densidade aparente de fórmula, unidades e exercícios resolvidos

O densidade aparente de uma amostra é definida como o quociente entre sua massa e o volume sem alterar, que inclui todos os espaços ou poros que ele contém. Se houver ar nesses espaços, densidade aparente ρ_b, qualquer Densidade aparente é:

ρ_b = Massa / volume = massa _partículas + Massa _ar /Volume _partículas+ Volume _ar

figura 1. A densidade aparente é muito importante para caracterizar os solos. Fonte: Wikimedia Commons.

Quando a densidade aparente de uma amostra de solo é calculada, ela deve estar secando anteriormente em um forno a 105 ° C até que a massa seja constante, indicativa de que todo o ar evaporou.

De acordo com esta definição, a densidade aparente dos solos ou Densidade seca, É calculado desta maneira:

ρ_s = Peso de elementos sólidos / volume _sólidos + Volume _poros

Denotando como m_s para o peso seco ou massa e V_t = V_s + V_p Como o volume total, a fórmula permanece:

ρ_s = M_s / V_t

[TOC]

Unidades

As aparentes unidades de densidade no sistema internacional de unidades são kg/m³. No entanto, outras unidades como G/CM³ e megagramos/medidor cúbico: mg/m³ Eles também são amplamente utilizados.

O conceito de densidade aparente é muito útil quando se trata de materiais heterogêneos e porosos, como os solos, pois é indicativo de sua capacidade de drenagem e aeração, entre outras qualidades.

Por exemplo, pequenos solos porosos têm altas densidades aparentes, são compactas e tendem a ser facilmente despertadas, ao contrário de solos porosos.

Quando há água ou outro líquido na amostra, o volume após a secagem diminui; portanto, no momento dos cálculos, é necessário conhecer a proporção de água original (veja o exemplo resolvido).

Densidade aparente do solo

A densidade aparente dos materiais em geral, incluindo o solo, é muito variável, pois existem fatores como o grau de compactação, a presença de matéria orgânica, sua textura, estrutura, profundidade e outros, que afetam a forma e a quantidade de espaços porosos.

Os solos são definidos como uma mistura heterogênea de substâncias inorgânicas, substâncias orgânicas, ar e água. Para o toque pode ser textura Fino, médio ou grosso, enquanto as partículas de componentes podem ser organizadas de várias maneiras, um parâmetro conhecido como estrutura.

Solos finos e bem estruturados e com uma alta porcentagem de matéria orgânica geralmente têm baixos valores de densidade aparente. Pelo contrário, solos grossos, com matéria menos orgânica e pouca estrutura, tendem a ter valores mais altos.

Pode servir a você: Teste de tensão: como é feito, propriedades, exemplos

Densidade aparente de acordo com a textura

De acordo com sua textura, a densidade aparente tem os seguintes valores:

Textura	Densidade aparente (g/cm3)
Multar	1.00 - 1.30
Mediana	1.30 - 1.cinquenta
Bruto	1.50 - 1.70

Esses valores servem como uma referência geral. Em solos turbósicos, abundantes em desperdício de plantas, a densidade aparente pode ser tão baixa quanto 0.25 g/cm³, Se for um solo mineral vulcânico, está em torno de 0.85 g/cm³, Enquanto em solos muito compactos, atinge 1.90 g/cm³.

Densidade aparente de acordo com a profundidade

O valor de densidade aparente também aumenta com a profundidade, uma vez que o solo geralmente é mais compactado e tem uma porcentagem menor de matéria orgânica.

O interior da terra é composto de camadas horizontais ou estratos, chamados Horizontes. Os horizontes têm texturas, composição e compactação diferentes. Portanto, eles apresentam variação na densidade aparente.

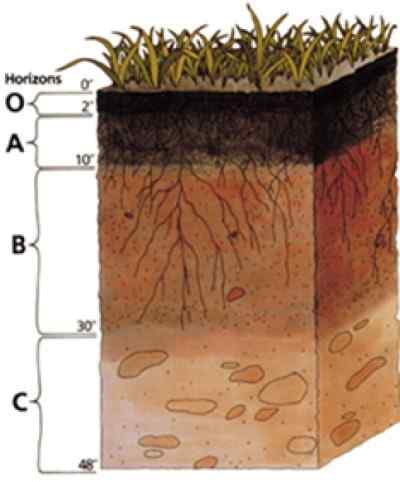Figura 2. Um perfil de solo mostrando os diferentes horizontes. Fonte: Wikimedia Commons.

Um estudo do solo é baseado em seu perfil, que consiste em vários horizontes que se seguem de maneira vertical.

Como medir densidade aparente?

Como a variabilidade na densidade aparente é muito grande, geralmente é necessário medi -la diretamente através de vários procedimentos.

O método mais simples consiste em extrair uma amostra do solo, introduzindo uma varredura com um cilindro de metal espacial de volume conhecido e certificando -se de não compactar o solo. A amostra extraída é selada, para evitar perda de umidade ou alteração das características.

Então, em laboratório, a amostra é extraída, pesada e depois colocada em um forno a 105 º C para secar por 24 horas.

Pode atendê -lo: corpos celestes

Embora seja a maneira mais simples de encontrar a densidade seca do solo, não é a mais recomendada para solos com texturas muito soltas ou cheias de pedras.

Para isso, o método de cavar um buraco é preferível e salvar a terra extraída, que será a amostra para secar. O volume da amostra é determinado derramando areia ou água seca no buraco do Cavado.

De qualquer forma, a partir da amostra, é possível determinar propriedades muito interessantes do solo para caracterizá -lo. O próximo exercício resolvido descreve como fazer isso.

Exercício resolvido

Uma amostra de argila de 100 mm de comprimento é extraída do cilindro de amostra, cujo diâmetro interno também é 100 mm. Com tristeza, é obtida uma massa de 1531 g, que uma vez seca é reduzida para 1178 g. A gravidade específica das partículas é 2.75. É solicitado para calcular:

a) A densidade aparente da amostra

b) teor de umidade

c) o relacionamento vazio

d) densidade seca

e) o grau de saturação

f) Conteúdo do ar

Solução para

O volume sem alterar V_t É o volume original da amostra. Para um diâmetro d e cilindro de altura H, o volume é:

V _cilindro = V_t = Área base x altura = πd²/4 = π x (100 x 10^-3 m)² x 100 x 10 ^-3 m/ 4 = 0.000785 m³

A declaração afirma que a massa da amostra é M_s = 1531 g, portanto, de acordo com a equação dada no início:

ρ_b = M_s / V_t  = 1531 g / 0.000785 m³ = 1950319 g/ m³ = 1.95 mg/m³

Solução b

Como temos a massa original e a massa seca, a massa da água contida na amostra é a diferença desses dois:

Pode servir a você: Processo isobárico: fórmulas, equações, experimentos, exercícios

M _água = 1531 g - 1178 g = 353 g

A porcentagem de umidade na amostra é calculada da seguinte forma:

% De umidade = (massa _água / Ms) x 100 % = (353 g / 1178 g) = 29. 97 %

Solução c

Para encontrar a proporção vazia, o volume total da amostra v deve ser quebrado_t em:

V _t = V _partículas + Volume _poros

O volume ocupado pelas partículas é obtido da massa seca e da gravidade específica, dados obtidos da declaração. A gravidade específica s_g É a razão entre a densidade do material e a densidade da água em condições padrão; portanto, a densidade do material é:

ρ = s_g x ρ_água = 2.75 x 1 g/cm³ = 2.75 g/cm³

ρ = m_s / V_s → v_s = 1.178 g / 2.75 g/cm³ = 0.428 cm³ = 0.000428 m³

O volume de lacunas na amostra é V_v = V_t - V_s = 0.000785 m³ - 0.000428 m³ = 0.000357 m³.

O relacionamento vazio e é:

e = v_v /V_s = 0.000357 m³ / 0.000428 m³ = 0.83

Solução d

A densidade seca da amostra é calculada conforme indicado na introdução:

ρ_s = Peso de elementos sólidos / volume _sólidos + Volume _poros= 1178 g/0.000785 m³ = 1.5 mg/m³

Solução e

O grau de saturação é s = (v_água / V_v ) X 100%. Como conhecemos a massa de água na amostra, calculada no item b) e sua densidade, o cálculo de seu volume é imediato:

ρ_água = M_água / V _água → v_água = 353 g / 1 g / cm³ = 353 cm³ = 0.000353 m³

Por outro lado, o volume de lacunas foi calculado no item c)

S = (0.000353 m³ / 0.000357 m³) x 100% = 98.9%

Solução f

Finalmente o conteúdo de ar percentual é A = (v_ar / V_t) X 100%. O volume de ar corresponde a:

V_v - V_água = 0.000357 m³ - 0.000353 m³ = 0.000004 m³

A = (v_ar / V_t) x 100% = (0.000004 m³/ 0.000785 m³) x100 % = 0.51 %

Referências

1. Berry, p. Mecânica de Solos. McGraw Hill.
2. Construmático. Densidade aparente. Recuperado de: Construmático.com.
3. NRCS. Densidade a granel do solo. Recuperado de: NRCs.USDA.Gov.
4. Unam. Departamento de Edafologia. Manual de procedimentos analíticos da física do solo. Recuperado de: geologia.Unam.mx.
5. Wikipedia. Densidade aparente. Recuperado de: em.Wikipedia.org.
6. Wikipedia. Chão. Recuperado de: em.Wikipedia.org.