Quais são os divisores de 30? (Explicação)

Os divisores de 30 são 1, 2, 3, 5, 6, 10, 15 e 30. Nós explicamos por que e como você pode calculá -lo por si mesmo.

Rapidamente, pode ser conhecido Quais são os divisores de 30, bem como qualquer outro número (diferente de zero), mas a idéia fundamental é aprender como os divisores de um número são calculados de uma maneira geral.

Deve -se tomar cuidado ao falar sobre divisores, porque pode -se estabelecer rapidamente que todos os divisores de 30 são 1, 2, 5, 6, 10, 15 e 30, mas e os negativos desses números? São divisores ou não?

Para responder à pergunta anterior, é necessário entender um termo muito importante no mundo da matemática: o algoritmo da divisão.

Algoritmo de divisão

O algoritmo de divisão (ou divisão euclidiana) diz o seguinte: Dados dois números inteiros "n" e "b", sendo "b" diferente de zero (b ≠ 0), existem "q" e "r" exclusivos, de modo que n = bq+r, onde 0 ≤ r < |b|.

O número "n" é chamado de dividendo, "b" é chamado de divisor, "q" é chamado de quociente e "r" é chamado de resto ou desperdício. Quando o resto "r" é igual a 0, diz -se que "B" divide "n", e isso é indicado por "B | n".

O algoritmo de divisão não se restringe a valores positivos. Portanto, um número negativo pode ser divisor de algum outro número.

Por que 7.5 não é um divisor de 30?

Usando o algoritmo de divisão, pode -se ver que 30 = 7,5 × 4+0. O resto é igual a zero, mas não se pode dizer que 7.5 divide 30 porque, ao falar sobre divisores, apenas números inteiros estão sendo discutidos.

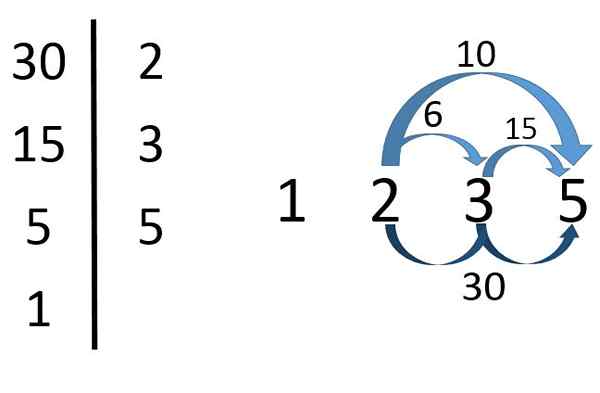Divisores de 30

Como pode ser visto na imagem, para encontrar os divisores de 30 primeiro, seus principais fatores devem ser encontrados.

Então, 30 = 2x3x5. Daqui concluiu que 2, 3 e 5 Eles são divisores de 30. Mas também os produtos desses fatores primos.

Para que 2 × 3 =6, 2 × 5 =10, 3 × 5 =quinze e 2x3x5 =30 Eles são divisores de 30. Ele 1 É também um divisor de 30 (embora na realidade seja um divisor de qualquer número).

Pode -se concluir que 1, 2, 3, 5, 6, 10, 15 e 30 são divisores de 30 (Todos cumprem o algoritmo da divisão), mas devemos lembrar que seus negativos também são divisores.

Portanto, todos os divisores de 30 são: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 e 30.

O que foi aprendido acima pode ser aplicado com qualquer número inteiro.

Por exemplo, se você deseja calcular os divisores de 92, prossiga como antes. Ele quebra como um produto de números primos.

92 é dividido por 2 e obtido 46; Agora 46 está dividido por 2 novamente e recebe 23.

Este último resultado é um número primo, por isso não terá mais divisores, além de 1 e os mesmos 23.

Podemos então escrever 92 = 2x2x23. Procurando como antes, conclui -se que 1,2,46 e 92 são 92 divisores.

Finalmente, os negativos desses números para a lista anterior estão incluídos, que é a lista de todos os divisores de 92 é -92, -46, -4, -2, -1, 1, 2, 4, 46, 46, 92.