Corpo rígido

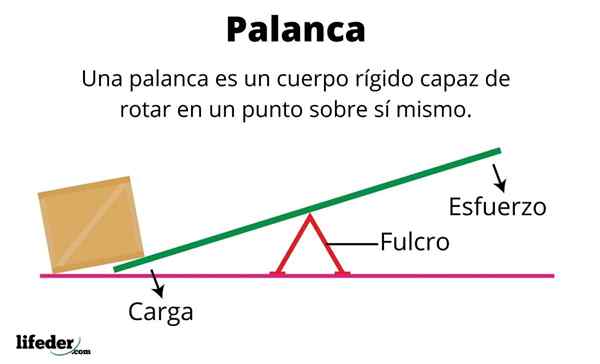
O que é um corpo rígido?

Um corpo rígido é um objeto material cujas partículas sempre permanecem nas mesmas posições relativas. Portanto, é um objeto que não é deformado, uma qualidade atribuída às intensas forças de coesão que mantêm as partículas no lugar.

Na verdade, as partículas de qualquer corpo sujeitas a forças externas tendem a vibrar ou se mover, de modo que o objeto é sempre se deforma até certo ponto, mas esses efeitos são geralmente pequenos.

Quando esse é o caso, pode -se supor que o corpo é rígido e tendo uma abordagem muito boa para seu comportamento, mesmo que seja uma idealização.

Tipos de corpos rígidos

Você pode distinguir dois tipos de corpo rígido:

• Aqueles cujas partículas vêm em quantidades discretas, ou seja, podem contar. Por exemplo, duas esferas de metal ligadas por uma haste fina e leve podem ser consideradas uma entidade única. Se a haste for rígida o suficiente para não dobrar, o sistema será considerado um corpo rígido.
• Aqueles que são contínuos, o que significa que as partículas que as compõem são indistinguíveis. Objetos todos os dias e da natureza são bons exemplos: pedras, móveis e outros, bem como a terra e outras rochas celestes rochosas.

Movimento corporal rígido e dinâmica

Como objetos considerados como partículas, corpos rígidos podem ser transferidos, girar e ter um movimento mais geral, combinando tradução e rotação.

Para estudar a tradução, não é necessário.

Esses movimentos de tradução e rotação podem ser:

• Independente, como no caso dos planetas, que têm um movimento de rotação ao redor de seu eixo (considerado fixo) e outra tradução ao redor do sol, mas as velocidades de cada um não estão relacionadas.
• Trilha quebrada, se a velocidade angular e a velocidade de tradução do centro de massa estiverem relacionadas. Nesse caso, o eixo de rotação é móvel, como no caso do cilindro que desce atirando sem escorregar por uma inclinação inclinada.

Pode servir a você: Primeira Lei da Termodinâmica: Fórmulas, Equações, Exemplos

A dinâmica de sólido rígido

As magnitudes a seguir são relevantes na dinâmica do sólido rígido:

Centro de massa

O centro de massa é o ponto em que toda a massa do corpo é considerada concentrada. Se é um corpo homogêneo e simétrico, como uma esfera, o centro de massa coincide com o centro geométrico.

O momento da inércia

Essa magnitude escalar é o valor da inércia rotacional ou resistência que se opõe a um objeto para girar em torno de um certo eixo. Depende inteiramente da geometria do objeto e de sua massa e, portanto, em certos casos, é mais fácil girar certos eixos do que em outros.

Para corpos com formas geométricas bem definidas, há mesas com os momentos de inércia em relação aos eixos de simetria, por exemplo, aquele que passa pelo centro de massa. Com essas informações e os teoremas relacionados ao momento da inércia, os momentos em relação a outros eixos podem ser facilmente calculados.

Forças e torque ou torque

As forças são obrigadas a mover um corpo. Se o rígido centro de massa sólido se mover, a equação do movimento, de acordo com a segunda lei de Newton, é:

F_Líquido = M ∙para_cm

Onde:

-A força líquida é F_Líquido

-M é a massa

-A aceleração do centro de massa é para_cm

No entanto, nem todas as forças aplicadas fazem o objeto quebrar. Para fazer isso, o torque ou o torque é necessário, o que diz quão eficaz é a ação rotacional de uma força. É definido como o produto vetorial entre o vetor de posição r Sobre um certo ponto e força F em questão. É denotado pela carta grega τ (Em letra ousada, também é um vetor):

Pode atendê -lo: movimento elíptico

τ = r × F

No sistema internacional, a unidade de torque é N⋅m (Newton por metro).

Em muitos casos, o movimento rotacional em torno de um eixo que passa pelo centro de massa é descrito por uma equação análoga à segunda lei de Newton:

Onde o subscrito "Z" refere -se ao eixo de rotação que passa por um eixo de simetria, fixo ou comovente, mas sem mudar de direção, e_cm É o momento da inércia em relação ao centro de massa e α_z É a aceleração angular do corpo. O verão cobre todos os momentos externos ao redor do eixo z.

Energia cinética de um sólido rígido

O movimento de um corpo rígido é descrito pelas traduções do centro de massa e rotações em torno desse ponto, portanto, sua energia cinética tem ambas as contribuições.

Deixe k a energia cinética do corpo, v_cm A velocidade do centro de massa, na massa do corpo, e_cm seu momento de inércia em relação ao centro de massa e ω a velocidade angular. Pode -se demonstrar que a energia cinética é:

K = ½ mV_cm² + ½ i_cm Ω²

Observa -se que o segundo termo à direita é o análogo rotacional do termo. Lá, o momento da inércia desempenha o mesmo papel que a massa, enquanto a velocidade angular tem o mesmo papel que a velocidade linear.

Exemplos na vida cotidiana

Pêndulo físico

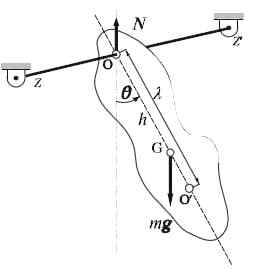Pêndulo físico

O pêndulo físico ou pêndulo real é muito fácil de construir: consiste em um sólido rígido como uma haste ou barra, oscilando livremente em torno de um eixo horizontal. O eixo de rotação não atravessa o centro de massa do objeto e isso em princípio pode ter qualquer forma.

Pode servir a você: Termômetro de resistência: características, operação, usos

Este pêndulo difere do pêndulo simples, porque neste último é considerado que a massa que compõe é pontual.

Roda de bicicleta

Roda de bicicleta

Outro exemplo corporal rígido bem conhecido é a roda de bicicleta, cujo eixo passa pelo centro de massa, que atravessa o centro da roda. Enquanto eles não se inclinam para o lado ou giram, as equações da dinâmica descrita se aplicam para descrever seu movimento.

Uma bola de boliche

Um bom exemplo de corpo rígido é a bola de boliche

O modelo sólido rígido se adapta muito bem para descrever o movimento da bola de boliche na pista ou quando rolar sem deslizar a rampa de retorno.

O yoyo

Yoyo é um brinquedo popular que pode ser modelado como um corpo rígido

Este brinquedo popular é feito com um cilindro de madeira ou plástico e uma corda sobrecarregada em um slot que o rodeia.

O cilindro pode ser modelado como um corpo rígido no qual a tensão na corda fornece o torque para a rotação, enquanto o peso (aplicado ao centro de massa) e a tensão são responsáveis ​​pela aceleração vertical do centro de massa.

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill. 
2. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
3.  Katz, d. 2013. Física para cientistas e engenheiros. Fundações e conexões. Cengage Learning.
4. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1. Pearson.
5. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.